笔记来源：bilibili

Transformer 的死穴

Transformer 结构的核心是自注意力机制层，无论是 encoder 还是 decoder，序列数据都先经过位置编码后喂给这个模块。

但是自注意力机制的计算范围仅限于窗口内，而无法直接处理窗口外的元素。因此，这种机制无法建模超出有限窗口的任何内容，看不到长序列的世界。

解决有办法：增加窗口的长度。但是，这样会导致计算复杂度随着窗口长度的增加而呈现平方增加 $O(n^2)$，因为每个位置的计算都需要与窗口内的所有其他位置进行比较。

Transformer 的本质：通过位置编码，把序列数据空间化，然后通过计算空间相关度反向建模时序相关度。可以看到，这个过程忽视了内存结构的细腻关联关系，而是采取了一种一视同仁的暴力关联模式。比如，一个句子中存在一定的语法，同时，一个句子中也可能存在冗余的信息。所以，Transformer 存在不易训练的问题。

时序数据，却使用空间化的注意力机制，在当时是为了充分利用 GPU 的并行能力，但这不是万能的。让长序列数据建模回归传统，某种程序上说，这是整个 SSM 类模型思考问题的初衷和视角，而 Mamba 是其中的佼佼者。

时序状态空间模型 SSM

连续空间的时序建模

有很多实际的问题都可以用左图所示的连续空间模型来建模，比如控制理论或线性系统领域。一般将其称为 LTI（linear time-invariant，线性时不变）系统，用公式表示就是：

$$h^{\prime }(t)=Ah(t)+Bx(t)$$
$$y(t)=Ch(t)$$
输入为 $x$，隐藏层的变量为 $h(t)$，$y(t)$ 为输出。上面的叫状态方程，下面的叫观测方程。ABCD 为参数矩阵。

之所以叫时不变，是因为，ABCD 是固定的，这是一个强假设（transformer 没有这样的假设）。D 在上面的式子中没写主要是因为在许多实际系统中，它可以是零。通过牺牲通用性，换来特定场景下的更高的性能，是所有 SSM 模型的最底层逻辑。

时序离散化与 RNN

连续系统不方便计算机的处理，所以要对它进行离散化展开，就是沿时间拉长，模型和 RNN 长相上几乎一样（上图中，中图所示）。

公式也类似，只是导数改为不同时刻角标，形成递归过程。

$$h_t=\bar{A}{h}_{y-1}+\bar{B}{x}_t$$
$$y_t=C{h}_t$$
原文给出了一种从连续系统转换为系统的 ABC 参数对应关系。它其实只是一种方法的举例，叫"零阶保持（Zero-Order Hold, ZOH）"。只用知道使用了一个 delta 函数，经过一组运算，可以提到新的 A 和 B。

$$\bar{A}=exp(\Delta A),\bar{B}=(\Delta A{)}^{-1}(exp(\Delta A)-I)\cdot \Delta B$$

从效果上看，就是从上面的连续的输入，变成了下面离散的输入。输出也是。

以上是零阶保持的效果图，变成阶跃式的了。

并行化处理与 CNN

SSM 的最大特点是可以通过卷积实现了计算上的并行化（上图中，右图所示）。

其核心的思想是使用 CNN 对时序数据建模，借助不同尺度的卷积核，从不同时间尺度上捕获时序特征。其公式表示为：
$$\bar{K}=(C\bar{B},C\overline{AB},...,C{\bar{A}}^k\bar{B},...)$$
$$y=x\ast \bar{K}$$
其图示为：

第二个式子与前面的图完全对应，就是一个 CNN 实现。时序递归状态方程改用卷积操作实现了，ABC 参数矩阵变成了 K ，就是图中的卷积核。体现在效果上，借助不同卷积核捕捉局部时间序列特征，可以同时对短期和长期依赖关系学习，并行计算提高了训练和推理的效率，使得 SSMs 在处理复杂的时序数据时表现出色。

在实际的问题中，往往会对 ABC 矩阵进一步简化，假设成更简单的对角阵来计算，这就是结构化 SSM，也叫 S4 模型。

在某种程序上，可以将 SSM 看成是 CNN 化的 RNN。

由于 SSM 有两个强假设：线性+时不变。所以极大的限制了其使用范围，因为大部分的系统是非线性，时变系统。而 Mamba 本质上是一个 SSM 模型的改进版，放开了这两个约束。

Mamba：选择性 SSM

Mamba 主要体现在设计了一种机制，让状态空间具备选择性，达到了 Transformer 的建模能力，同时在序列长度上实现了线性扩展（克服了 Transformer 的缺陷），可处理最长达百万长度的序列，而且效率很高，准确率很好。

在时间序列模型中设计了一个类似于 LSTM 的门结构，实现了选择性。BC 都带了 t，变成了时变参数，A 虽然没有直接含 t，但是通过 ${\Delta }_t$ 也变成了时变的，${\Delta }_t$ 就是前面的离散函数。下面的蓝色部分就是所谓的选择机制。

最简单的理解就是：一个总开关（${\Delta }_t$）+若干个旋钮（$B_t,C_t$ ）=非线性时变系统。

要解决的问题

从某种角度看，序列建模的核心就是研究如何将长序列的上下文信息压缩到一个较小的状态中。比如，语言模型实际上就是在一个有限的词汇集合中不断进行转换。Transformer 的注意力机制虽然有效，但是效率低，因为它要存储整个上下文，导致推理和训练的时间较长。而 SSM 递归模型的状态是有限的（单纯是时不变导致的），其效率高但是有效性受限于状态的压缩能力。

而 Mamba 就是平衡了有效性与效率的点。本文关注了两种能力：

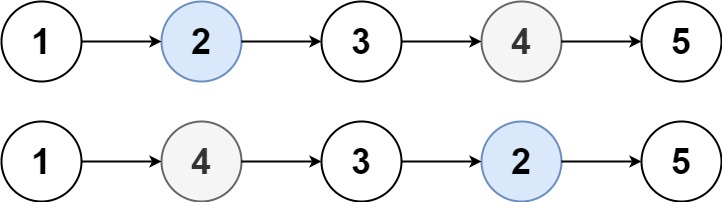
一是抓重点的能力（选择性复制任务）：从大量的信息中选择和记住关键的信息，忽略不相关的部分。类似于在一个文章中找到关键词：

二是上下文联想，推理能力（诱导头任务）。在处理连续的信息时，能保持逻辑一致性和上下文的连贯性。

具体的改进的方法：由于 B 是时不变的（强假设的 LTI 系统），所以这导致了难以有效的选择上下文信息：无论输入的 x 是啥，B 一直不变（B （网络）与 x 无关）。所以，改进的方法就是让它时变：

全局卷积虽然可以用不同的卷积核进行时序特征捕捉，但是缺乏内容感知：不知道输入的重点与逻辑。但是 transformer 没有这些限制：既不是时不变系统，也不是线性系统。所以改进的方法就是：将其改成时变系统，并且改成非线性系统。

增加选择性的方法

增加选择性的本质是将 B 和 C 由固定的变成了可变的，根据输入 $x_t$ 和它的压缩投影学习可变参数。A 为了简化，其自身还是不变的。蓝色部分（包括投影和连线）（上图所示）就是所谓的选择机制。目的是根据输入内容选择性地记忆和处理信息，从而提高对复杂序列数据的适应能力。

由于 ${\Delta }_t$ 使用了 $\tau$ 激活函数，所以是非线性的，而 ${\Delta }_t$ 对 $B_t$，$A$，$C_t$ 都有作用，所以整个系统都是非线性时变的。所以整个系统的两个条件都放开了。

右侧公式中，投影出来的三条划线其实就是 $S_B,S_C,S_{\Delta }$ 三个选择函数，共享一个投影模块，主要是为了实现参数共享和计算效率。

而左侧就是原来的算法，可以看到：ABC 和 $\Delta$ 都是固定的。

所以，Mamba 的本质上是拿 LSTM 的门控思想换票到了 SSM 模型上，放开了时不变的约束放成非线性系统。

参数：

• B：批次大小。表示一次输入的数据量的大小
• L：序列长度。表示每个序列中包含的时间步数
• N：特征维度。表示每个时间步的特征数量
• D：输入特征维度

其中，步长大小 delta 像是一个观察窗口，会影响信息处理的焦点。步长较小时，模型倾向于忽略具体的单词，而更多地依赖之前的上下文信息。

当 focus 较小时，只能看到几个词。所以，这个就可以理解为，delta 实现了注意力的选择。

上图代码中的几个选择函数：

• $S_B(x)=Linea{r}_N(x),S_C(x)=Linea{r}_N(x)$ 都是线性投影，这是很常见的神经网络操作，用于将输入数据转换到一个新的空间或维度。Linear 为线性层。
• $S_{\Delta }(x)=Broadcas{t}_D(Linea{r}_1(x))$，广播是一个数据操作，它使得维度较小的数组可以与维度较大的数据进行算术操作。
• ${\tau }_{\Delta }=softplus$，这是一个平滑的非线性函数，通常用于网络中以添加非线性特征并帮助网络学习复杂的模式。

经过这样的设计，希望达到的效果：

左侧为 LTI 系统，输出只能对规则的输入特征进行原样的复制，而右边的选择性系统则可以自己找重点了。同时，右侧也有联想的能力了。对于非线性时变数据，具备了很强的特征捕捉能力。

核心原理：液体力学与李指数映射

Transformer 描述的是粒子运动，通过自注意力机制映射动态调整每个输入的权重，类似粒子间通过牛顿力学相互作用力来动态调整自己的轨迹。训练的过程，就是在用牛顿力学拟合粒子轨迹。每个输入（粒子）独立计算与其他输入的关系。

而 Mamba 描述的是液体运动，通过李指数映射来建模时空结构。流体运动描述的是连续介质中的分子集体行为，运动是整体的，内部各点之间有强烈的相互关系和依赖。液体的每个部分都受到整体液体运动的影响，通过内部压力，粘性等因素相互作用。这更符合记忆的本质，因为记忆系统具有连续性，动态变化性和整体关联性，这些特性与液体的性质非常相似。液体模型可以更好地描述记忆中的信息如何相互关联，如何随着时间和新信息的出现进行动态调整和整合。

李指数映射是一种数学工具，用于描述和分析一个向量场如何沿着另一个向量场发生变化，比如液体力学，电磁场，广义相对论的时空结构等，解决了动态系统中相互作用的描述。它是和微分任何中重要的概念，来源于李群和李代数的理论。

如果把记忆的流淌比作一个水流管道系统，可以看做一个李群，进行各种复杂变换（旋转，推移等）。固定矩阵 A 就是主管道（全局演变路径），类似于液体运动的全局关系，让系统状态更新有固定的全局路径和规则，因此可以表现出更高的灵活性和适应性。而 $B_t$ 和 $C_t$ 就是阀门或旋钮，delta 这个离散化因子，就像是液体力学中的时间步长，决定液体运动的离散时间点。选择机制就像是根据具体情况选择和调整旋钮，控制流体在管道中的流动路径。

训练 Mamba 的过程就是李指数映射假使流体力学动态系统，找到主管道 A，调整阀门和旋钮 $B_t,C_t,\Delta t$ 获得最优流体流动路径，让模型可以在高维特征空间中进行高效导航和决策。

Transformer 的自注意力机制粒子运动强调个体的独立性和动态调整，灵活性高，能动态调整权重，捕捉复杂的上下文依赖关系，但计算复杂度高，资源消耗大。Mamba 流体运动强调整体的连续性和全局关系，借用独特的矩阵 A 的固定性，提供了稳定性和确定性，通过李指数映射实现高效状态更新和决策。