LLM时代的transformer参数量、计算量、激活值的分析

news2024/9/25 7:24:54

导读：本文可以看作是对分析transformer模型的参数量、计算量、中间激活、KV cache的详细说明

定性分析

GPU上都存了哪些东西

首先我们来从全局整体的角度看一看，在训练阶段GPU显存上都有哪些内容：

  • Model States：模型训练过程中必须存储的states
    • params（下面有时也叫做weights）：模型参数，记参数量为 Φ \Phi Φ
    • grads：模型梯度，梯度数量同参数量 Φ \Phi Φ
    • optimizer states：Adam优化器中的momentum和variance，数量分别是 Φ \Phi Φ，共 2 Φ 2\Phi 2Φ
  • Residual States：模型训练过程中，中间临时的、动态产生的states
    • activation：中间激活值，这个部分可能在训练过程中占据很大一部分显存，下面会详细分析。但是激活值不是必须存储的，可以使用重计算（recompute，也叫做activation checkpoint），在反向算梯度的时候，再重新算一遍，当然计算增加了，时间换空间，实际使用中可以部分选择性的进行重计算。
    • temporary buffers：临时存储，比如cuda、nccl等临时申请的显存。
    • unusable fragment memory：内存碎片导致的内存浪费

推理阶段就相对简单一些，最主要的是Model States中的params和Residual States中的activation。

参考：图解大模型训练之：数据并行下篇( DeepSpeed ZeRO，零冗余优化)

混合精度训练

上面只是列出了训练过程中，显存中存放的内容和保存的数值数量，但是实际训练过程中，为了节省显存，以及考虑到训练过程中间某些过程对精度不是特别敏感，所以中间有些部分会使用fp32，有些部分会使用fp16/bf16。下面以Megatron为例，简单分析混合精度训练的一个大致流程。

首先我们来看一下不使用混合精度训练的场景，数值精度全使用fp32，作为一个分析的baseline。具体过程是：

fp32精度训练

占用显存为： 4 Φ 4\Phi 4Φ（fp32 weights）+ 4 Φ 4\Phi 4Φ（fp32 momentum）+ 4 Φ 4\Phi 4Φ（fp32 variance）+ 4 Φ 4\Phi 4Φ（fp32 grad）+fp32 activation（可能很大）= 16 Φ 16\Phi 16Φ Bytes + fp32 activation（4代表fp32的4Bytes，2代表fp16/bf16的2Bytes）

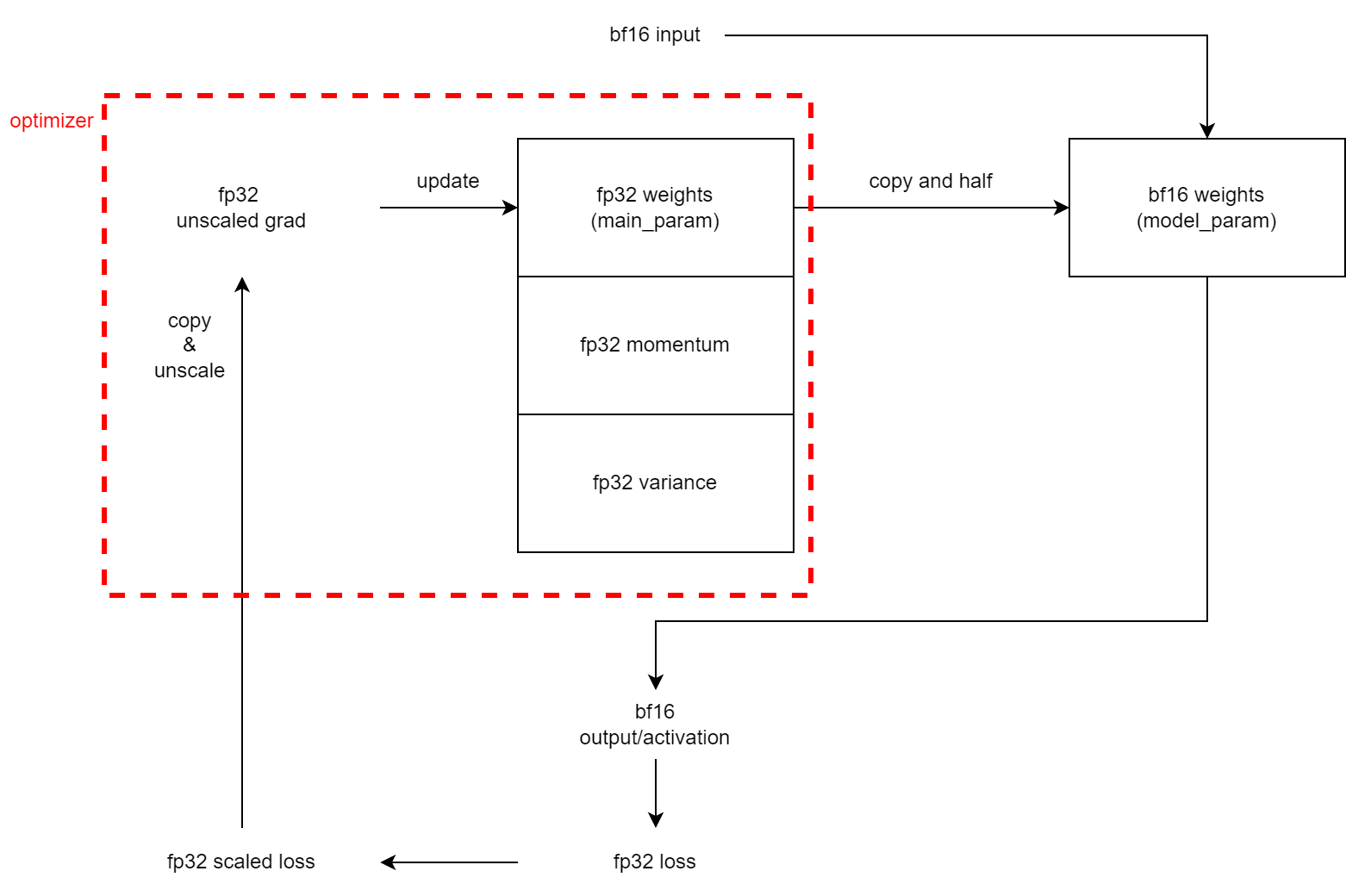
如果使用fp16的混合精度训练（bf16应该也可以，但是实际Megatron有点不同，下面会提到），具体过程是：

fp16混合精度训练

占用显存为： 4 Φ 4\Phi 4Φ（fp32 weights）+ 4 Φ 4\Phi 4Φ（fp32 momentum）+ 4 Φ 4\Phi 4Φ（fp32 variance）+ 2 Φ 2\Phi 2Φ（fp16 grad）+ 2 Φ 2\Phi 2Φ（fp16 scaled grad）+ 4 Φ 4\Phi 4Φ（fp32 unscaled and cliped grad）+fp16 activation（可能很大）= 20 Φ 20\Phi 20Φ Bytes + fp16 activation

需要说明的有两点：

  1. 当fp16 scaled grad转为为fp32 unscaled and cliped grad后，fp16 scaled grad就没用了，但是此时Megatron中仍然保留着一份fp16 scaled grad，所以显存占用中这两部分都会计算在内，这也符合Megatron offical readme中的描述：
image-20240907213340085

  1. 注意到上面流程中多了一个scale/unscale的操作，这叫做“loss scaling”

    ​ 在使用混合精度训练时，如果直接使用fp16的grad来更新fp16的梯度，一是会产生舍入误差（比如梯度很小，权重更新后，由于精度不够，累加上的lr * grad被舍入，权重没变，一句话来说就是大数吃小数），二是会产生梯度下溢（比如梯度过小，fp16范围不够，导致很小的梯度下溢成为0，而这样的小梯度占比很大，一句话来说就是下溢成0）。对于舍入误差，可以在更新权重时，将fp16的梯度转换为fp32，再更新fp32的权重，从而避免精度问题。对于梯度下溢，需要使用loss scale。

    ​ loss scale就是FWD计算出loss后，对loss放大若干倍，由于求导的链式法则，放大的若干倍同样会传导到fp16梯度，这样fp16梯度就不会产生梯度下溢。在更新权重时，将fp16的梯度转换为fp32，同时进行unscale。

刚才说到bf16有一点点特殊，我们看相应的代码：（Megatron中的arguments.py）

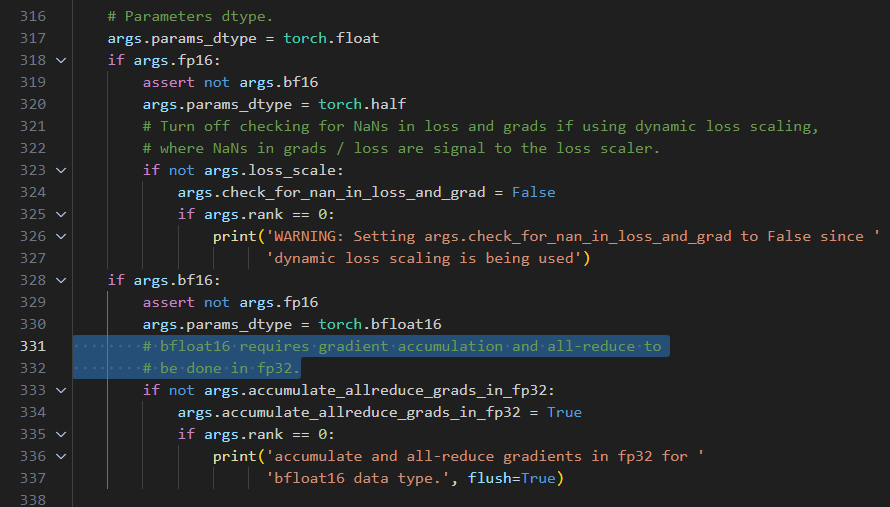
image-20240907214939077

注意到如果使用bf16，那么会强行设置accumulate_allreduce_grads_in_fp32=True，这与上面Megatron offical readme截图（Distributed Optimizer）表格中的第二行【bf16 param, fp32 grads】相对应。具体过程应该是（not for sure, hope for discuss）：

accumulate_allreduce_grads_in_fp32：If true, do the gradient accumulation and communication in fp32. from here

gradient accumulation：在若干次iteration中，每次都会反向得到一份梯度，将这若干次iteration得到的梯度进行累加、求平均，在最后一次iteration才更新权重。gradient accumulation与data parallel是等价的，gradient accumulation在时间维度上训练多个mini-batch，而data parallel在相同时间内将不同mini-batch放在不同的机器上训练，结果都是一样的。

参考：

  • 聊聊梯度累加(Gradient Accumulation)

  • 梯度累积算法

  • Hugging Face:Performing gradient accumulation with 🤗 Accelerate

bf16混合精度训练

这里找到一个为什么要将bf16与accumulate_allreduce_grads_in_fp32绑定的issue，里面提到“We found this to lead to more stable training before, but you could also try to perform the all-reduce in bf16 (it might hurt convergence but will be faster).”

参考：

  • 图解大模型训练之：数据并行下篇( DeepSpeed ZeRO，零冗余优化)
  • 图解大模型训练系列之：Megatron源码解读3，分布式混合精度训练
  • NVIDIA Docs Hub：Train With Mixed Precision
  • 全网最全-混合精度训练原理

量化分析

transformer结构详解

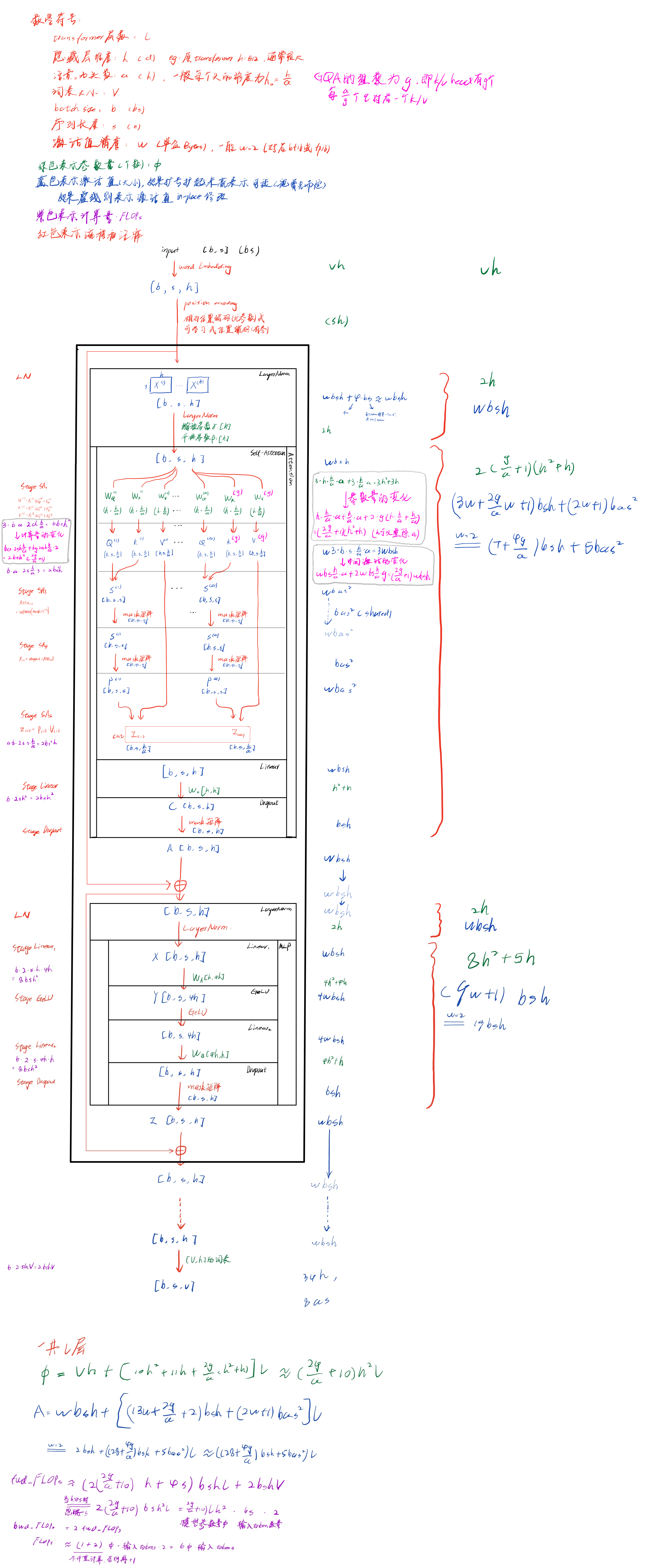
LLM中的transformer一般是decoder-only结构，所以下面的transformer block主要是decoder，但是与Vanilla Transformer中的decoder不同的是，这里没有了cross-attn，因此结构看起来反而有点像encoder（但不是，因为有casual mask）。

下面图中的Transformer，没有上kv-cache、GQA等优化，这部分后面会分析。其中，参数量 Φ \Phi Φ表示有多少个参数；中间激活值 A A A的单位是Bytes，主要参考的是分析transformer模型的参数量、计算量、中间激活、KV cache

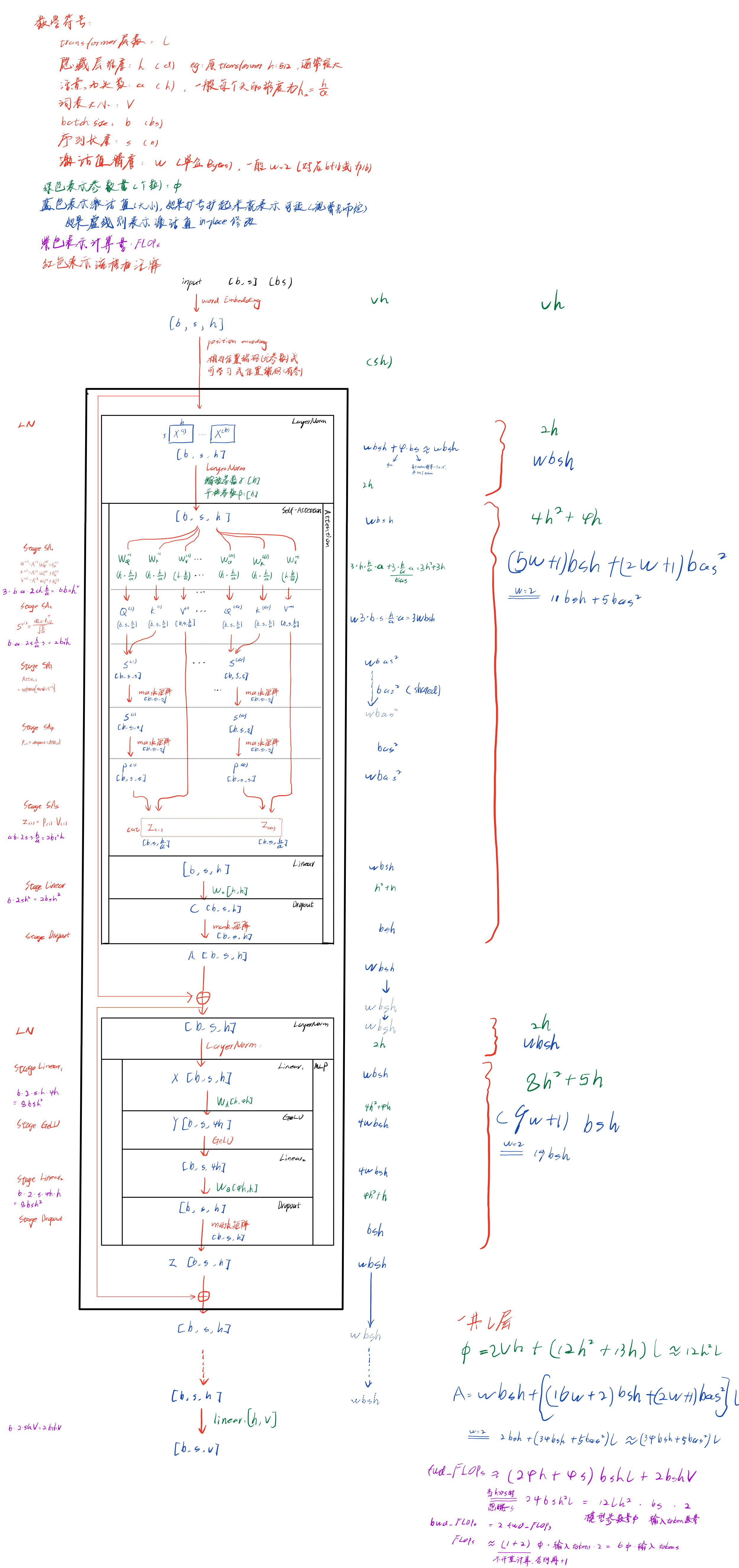
transformer详细分析

在Reducing Activation Recomputation in Large Transformer Models 4.1节中也对transformer激活值进行了一个分析，但是该论文中，self-attention block部分softmax之前没有加mask，上图中添加了mask，具体在Attention部分stage SA_3，其中mask由于是整个transformer共享的，所以就省略了， Q K T QK^T QKT的乘积被mask原地修改，所以 w b a s 2 wbas^2 wbas2也省略了，这样激活值与原论文中仍然是一样的。

KV cache对参数量、计算量、激活值的影响

关于KV Cache的来龙去脉，Encoder Decoder和decoder Only架构训练和推理浅析中简单捋了一下。简单来说，kv cache在推理过程中使用，而且模型只能是decoder-only架构。由于自回归的方式逐token生成，self-attention部分必须使用casual mask，因此Q矩阵部分只需要计算最新token的q向量即可，K、V矩阵部分只需要拼接新token的k、v向量即可：

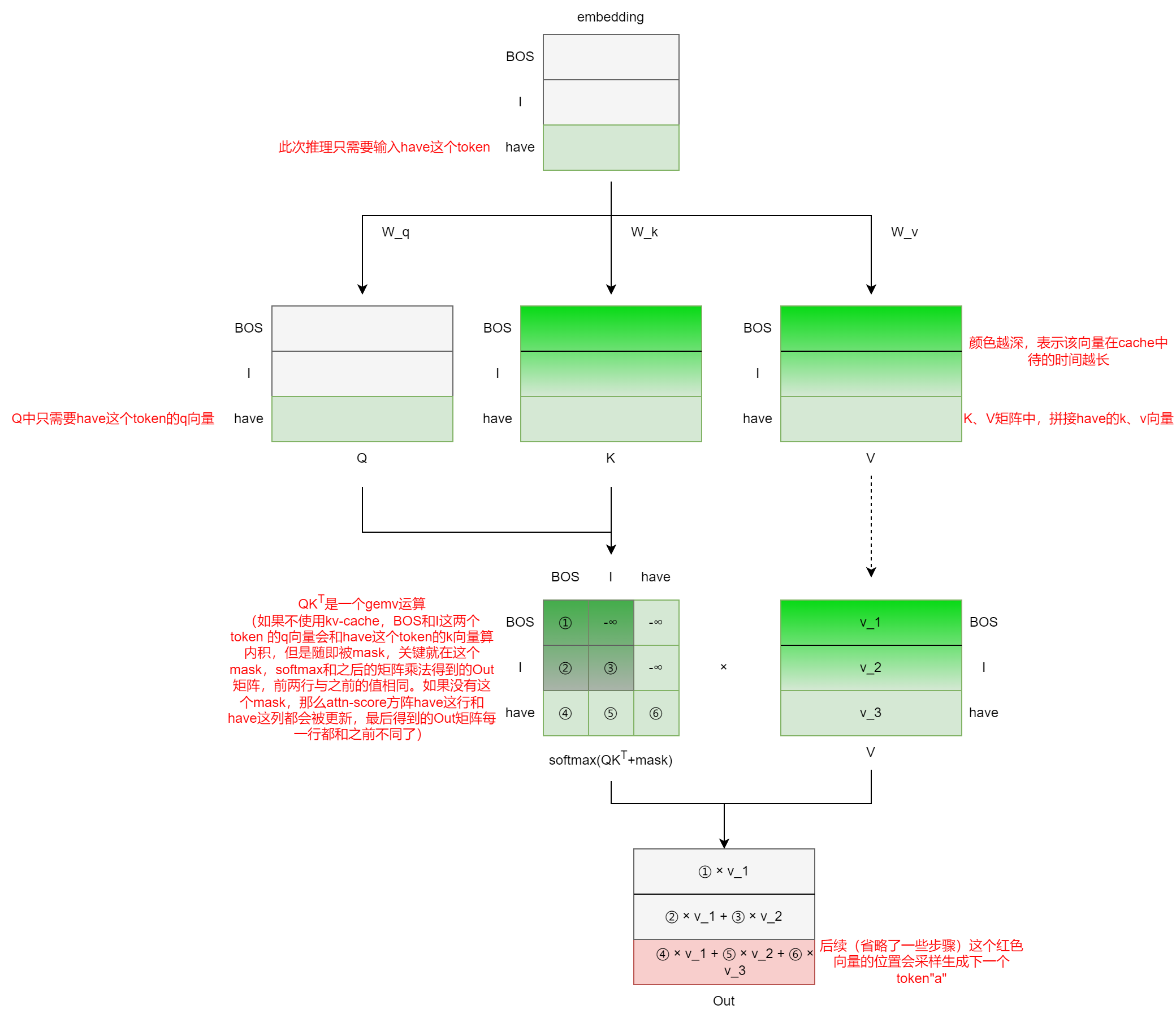
kv_cache

上面又重新回顾了一下kv cache。首先kv cache不会对参数量有影响，kv cache主要是用来减少不必要的计算的，显存因此也可能有相应的减少，上面只是一个示意图，中间省略了一些部分，详细的量化分析见下图，需要说明的有两点：

  1. kv cache使用场景是推理场景，LLM推理分为prefill阶段和decode阶段，prefill阶段创建kv-cache，decode阶段更新kv-cache。在输入prompt的这个prefill阶段中，with kv-cache和without kv-cache的计算量是相同的（显存占用由于分配kv-cache，可能with kv-cache会更多一点）。计算量的减少主要体现在decode阶段，因此下面的分析主要是针对单次decode阶段的，因此固定 s = = 1 s==1 s==1
  2. 下图中说的“相对于原来“指的是without kv-cache时，每次都输入之前所有的token，计算完整的attention-score方阵，因而此时的序列长度 s = s n ≤ s m s=s_n \le s_m s=sn​≤sm​。在最终分析时，取最大值 s = s m s=s_m s=sm​进行比较，对应decode阶段的最后一个token的生成过程，有的博客可能会将输入序列长度（prompt长度）和输出序列长度分开，这里合起来了，注意区别。
transformer详细分析（kv cache）
原来（without kv-cache）现在（with kv-cache）变化
参数量 2 V h + ( 12 h 2 + 13 h ) l 2Vh+(12h^2+13h)l 2Vh+(12h2+13h)l 2 V h + ( 12 h 2 + 13 h ) l 2Vh+(12h^2+13h)l 2Vh+(12h2+13h)l不变
中间激活 2 b s h + ( 34 b s m h + 5 b a s m 2 ) l 2bsh+(34bs_mh+5bas_m^2)l 2bsh+(34bsm​h+5basm2​)l 2 b s h + ( 30 b h + 4 b s m h + 5 b a s m ) l 2bsh+(30bh+4bs_mh+5bas_m)l 2bsh+(30bh+4bsm​h+5basm​)l减少了 ( 30 b h ( s m − 1 ) + 5 b a s m ( s m − 1 ) ) l (30bh(s_m-1)+5bas_m(s_m-1))l (30bh(sm​−1)+5basm​(sm​−1))l，原来中间激活是最长序列长度 s m s_m sm​的二次方，现在随着 s m s_m sm​线性增长
计算量 ( 24 h + 4 s m ) b s m h l + 2 b s m h V (24h+4s_m)bs_mhl+2bs_mhV (24h+4sm​)bsm​hl+2bsm​hV ( 24 h + 4 s m ) b h l + 2 b h V (24h+4s_m)bhl+2bhV (24h+4sm​)bhl+2bhV减少了 ( 24 h + 4 s m ) b h l ( s m − 1 ) + 2 b h V ( s m − 1 ) (24h+4s_m)bhl(s_m-1)+2bhV(s_m-1) (24h+4sm​)bhl(sm​−1)+2bhV(sm​−1)，原来计算量是最长序列长度 s m s_m sm​的二次方，现在随着 s m s_m sm​线性增长

code: from 【手撕LLM-KVCache】显存刺客的前世今生–文末含代码

# author: xiaodongguaAIGC
# KV-Cache + Generation + decoder 

import torch
import torch.nn.functional as F
from transformers import LlamaModel, LlamaConfig, LlamaForCausalLM

D = 128 # single-head-dim
V = 64  # vocab_size

class xiaodonggua_kv_cache(torch.nn.Module):
    def __init__(self, D, V):  
        super().__init__()
        self.D = D
        self.V = V
        self.Embedding = torch.nn.Embedding(V,D)
        self.Wq = torch.nn.Linear(D,D)     
        self.Wk = torch.nn.Linear(D,D)     
        self.Wv = torch.nn.Linear(D,D)
        self.lm_head = torch.nn.Linear(D,V) # LM_head
        self.cache_K = self.cache_V = None  # initial
        
    def forward(self,X):
        X = self.Embedding(X)
        Q,K,V = self.Wq(X),self.Wk(X),self.Wv(X)
        print("input_Q:", Q.shape)
        print("input_K:", K.shape)
        print("input_V:", V.shape)
        
        # Easy KV_Cache
        if self.cache_K == None: # first time
            self.cache_K = K
            self.cache_V = V
        else:
            self.cache_K = torch.cat((self.cache_K, K), dim = 1)
            self.cache_V = torch.cat((self.cache_V, V), dim = 1)
            K = self.cache_K
            V = self.cache_V
        
        print("cache_K:", self.cache_K.shape)
        print("cache_V:", self.cache_K.shape)
        
        # ignore proj/MLP/scaled/mask/multi-head when calculate Attention
        attn =Q@K.transpose(1,2)@V
        
        # output
        output=self.lm_head(attn)
        return output

model = xiaodonggua_kv_cache(D,V)
        
# 创建数据、不使用tokenizer
X = torch.randint(0, 64, (1,10))
print(X.shape)

for i in range(4):
    print(f"\nGeneration {i} step input_shape: {X.shape}：")
    output = model.forward(X) 
    print(output.shape)
    next_token = torch.argmax(F.softmax(output, dim = -1),-1)[:,-1]
    print(next_token.shape)
    X = next_token.unsqueeze(0)

reference and more reading：

【大模型理论篇】Transformer KV Cache原理深入浅出

大模型推理优化技术-KV Cache

一文读懂KVCache

MQA和GQA对显存占用的影响

在实际推理场景中，kv-cache已经是默认的选项。但是kv-cache是很占显存的，占用显存为 2 w k v b s m ( a h a ) l 2 w_{kv} b s_m (a h_a) l 2wkv​bsm​(aha​)l（其中 h = a ∗ h a h=a * h_a h=a∗ha​），后面会有case study分析。针对kv cache的各种优化层出不穷，下面的参考中有几篇博客总结了一下对kv cache的各种优化，简单来说，从上面的显存分析入手，有以下几种优化方法：

  • 针对attention 窗口（或者叫做context，上下文，或者当作最长序列长度 s m s_m sm​） s m s_m sm​的优化，比如window attention，sparse attention，StreamingLLM
  • 针对注意力头 a a a的优化，比如MQA，GQA共享kv-cache（sharing）
  • 针对层数 l l l的优化，比如YOCO层间共享kv-cache（sharing）
  • 针对精度 w k v w_{kv} wkv​的优化，比如kv-cache采用int8量化
  • 针对内存分配的优化，减少内存碎片等，比如PagedAttention
  • 其他优化。。。

其中MQA/GQA在LLM中广泛使用，比如Llama2中就使用到了GQA。下面简单分析一下。

GQA方法很简单，原来MHA中每个q向量对应一个k向量和v向量，进行attention计算；现在好几个q向量对应（或者说共享）一个k向量和v向量，这“好几个q向量”构成一组，一共有g组，每组就有 a g \frac{a}{g} ga​个q向量。如果g=1，那么就是MQA，a个q向量构成一组，共享一个k、v向量；如果g=a，那么就是MHA，每个q向量构成一组，对应一个k、v向量。实际场景中，往往g=8，比如推理场景中单卡放不下，正好单机八卡，每张卡对应一组q向量。

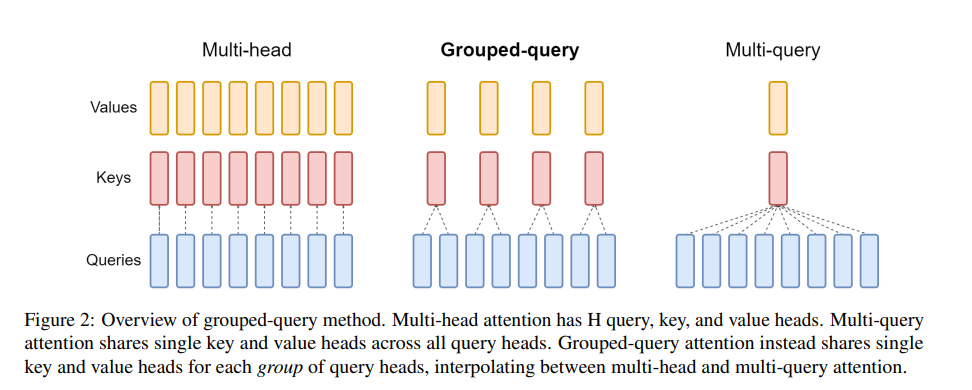
image-20240908164016647

虽然MQA/GQA是针对推理过程中kv-cache的优化，但是在训练中也能用，也能省显存。下面对GQA在推理场景中的使用（with kv_cache）进行一个量化分析。

image-20240908172449500

因为GQA只影响self-attention计算部分，因此其他部分省略，下面的表格也是只分析这个变化的部分。可以看出，由于kv-cache在长序列的情况下会占用很多显存，GQA针对中间激活的优化与序列长度相关，实际上GQA对中间激活的优化就是将kv-cache变为原来的 g a \frac{g}{a} ag​倍。

原来（MHA）-现在（GQA）说明
参数量 [ 3 ( h 2 + h ) ] l − [ ( 2 g a + 1 ) ( h 2 + h ) ] l = 2 ( 1 − g a ) ( h 2 + h ) l \left [3(h^2+h) \right ]l - \left [ (\frac{2g}{a}+1)(h^2+h) \right ]l=2(1-\frac{g}{a})(h^2+h)l [3(h2+h)]l−[(a2g​+1)(h2+h)]l=2(1−ag​)(h2+h)l
中间激活 [ w b s h + 2 w k v b s m h ] l − [ w b s h + 2 w k v b s m h × g a ] l = 2 w k v b s m h l ( 1 − g a ) \left [ wbsh+2w_{kv}bs_mh \right]l - \left [ wbsh + 2w_{kv}bs_mh \times\frac{g}{a} \right ]l = 2w_{kv}bs_mhl(1-\frac{g}{a}) [wbsh+2wkv​bsm​h]l−[wbsh+2wkv​bsm​h×ag​]l=2wkv​bsm​hl(1−ag​)尤其当长序列（ b s m bs_m bsm​较大），大模型（ h l hl hl较大）时，前面系数较大，整体激活减少比较可观
计算量$\left [ 6bsh^2 \right ]l - \left [ 2bsh^2 (\frac{2g}{a}+1) \right ] l = 4bsh^2l(1-\frac{g}{a}) \overset{s=1}{=} 4bh^2l(1-\frac{g}{a}) $

在训练场景中，同样给出量化分析。需要说明的是，上述分析是在推理场景+kv_cache+GQA的情况下进行的分析，下面公式是针对的是训练场景+GQA。

transformer训练场景分析（GQA）

code： from MHA，MQA，GQA注意力

import torch
import torch.nn as nn


class GroupedQueryAttention(nn.Module):
    def __init__(self, embed_dim, num_heads, num_groups):
        super().__init__()
        self.num_heads = num_heads
        self.num_groups = num_groups
        self.head_dim = embed_dim // num_heads
        # attention weights
        self.wq = nn.Linear(embed_dim, embed_dim)
        self.wk = nn.Linear(embed_dim, num_groups * self.head_dim)
        self.wv = nn.Linear(embed_dim, num_groups * self.head_dim)
        self.wo = nn.Linear(embed_dim, embed_dim)

    def split_heads(self, x: torch.Tensor, num_groups=None):
        # n == num_heads or num_groups
        x = x.view(x.size(0), x.size(1), -1, self.head_dim)  # (batch_size, seq_len, n, head_dim)
        batch_size, seq_len, n, head_dim = x.size()
        if num_groups is not None:
            x = x.unsqueeze(dim=2)
            x = x.expand(size=(batch_size, seq_len, self.num_heads // num_groups, n, head_dim))
            x = x.reshape(batch_size, seq_len, self.num_heads, head_dim)
        x = x.permute(0, 2, 1, 3)  # (batch_size, num_heads, seq_len, head_dim)
        return x

    def merge_heads(self, x: torch.Tensor):
        """
        :param x: (batch_size, num_heads, seq_len, head_dim)
        """
        x = x.permute(0, 2, 1, 3).contiguous()  # (batch_size, seq_len, num_heads, head_dim)
        x = x.view(x.size(0), x.size(1), -1)  # ( batch_size, seq_len, embed_dim)
        return x

    def forward(self, hidden_states: torch.Tensor, causal_mask=None):
        q, k, v = self.wq(hidden_states), self.wk(hidden_states), self.wv(hidden_states)
        # 分割注意力头
        q = self.split_heads(q)
        k = self.split_heads(k, num_groups=self.num_groups)
        v = self.split_heads(v, num_groups=self.num_groups)
        # 注意力计算
        attn_weights = torch.matmul(q, k.transpose(-1, -2)) / torch.tensor(k.size(-1), dtype=q.dtype)
        # causal mask
        mask_value = torch.finfo(attn_weights.dtype).min
        if causal_mask is None:
            seq_len = hidden_states.size(1)
            causal_mask = torch.tril(torch.ones((1, 1, seq_len, seq_len), dtype=torch.bool))
        attn_weights = torch.where(causal_mask, attn_weights, mask_value)
        # 归一化
        attn_weights = torch.softmax(attn_weights, dim=-1)
        attn_output = torch.matmul(attn_weights, v)
        # 合并注意力头
        attn_output = self.merge_heads(attn_output)
        attn_output = self.wo(attn_output)
        return attn_output

参考：

大模型百倍推理加速之KV cache篇

LLM（二十）：漫谈 KV Cache 优化方法，深度理解 StreamingLLM

[KV Cache优化]🔥MQA/GQA/YOCO/CLA/MLKV笔记: 层内和层间KV Cache共享

大模型推理加速：KV Cache 和 GQA

case study

我们以GPT和Llama为例，进行case study。

关于参数量的分析

GPT-3

GPT-3模型结构就大致上面【transformer结构详解】中的结构，但是多了一个可学习的position embedding，包含 n c t x ∗ h n_{ctx} * h nctx​∗h个参数，其中 n c t x = 2048 n_{ctx}=2048 nctx​=2048，rectified这一列是加上这些参数后的参数量。

paramshlabV from GPT-2calculated params= V h + ( 12 h 2 + 13 h ) l Vh+(12h^2+13h)l Vh+(12h2+13h)lrectified
GPT-3 Small: 125M76812640.5M50257123651840 ≈ \approx ≈ 123.7M125224704 ≈ \approx ≈ 125.2M
GPT-3 Medium: 350M102424640.5M50257353772544 $\approx$353.8M355869696 ≈ \approx ≈ 355.9M
GPT-3 Large: 760M153624960.5M50257757151232 ≈ \approx ≈ 757.1M760296960 ≈ \approx ≈ 760.3M
GPT-3 2.7B256032801M502572646305280 ≈ \approx ≈ 2.64B2651548160 ≈ \approx ≈ 2.65B
GPT-3 6.7B4096321282M502576650007552 ≈ \approx ≈ 6.65B6658396160 ≈ \approx ≈ 6.67B
GPT-3 13B5140401282M5025712942401780 ≈ \approx ≈ 12.94B12952928500 ≈ \approx ≈ 12.95B
GPT-3 175B12288961283.2M50257174579068928 ≈ \approx ≈ 174.58B174604234752 ≈ \approx ≈ 174.60B

说明：

  1. GPT-3词表大小V在论文中没找到，所以用的GPT-2的词表大小，这里论文中是提到的

more relative reading：

  • How does GPT-3 spend its 175B parameters?
Llama 1: LLaMa: Open and Efficient Foundation Language Models

模型结构：from hugging face transformers LLaMA

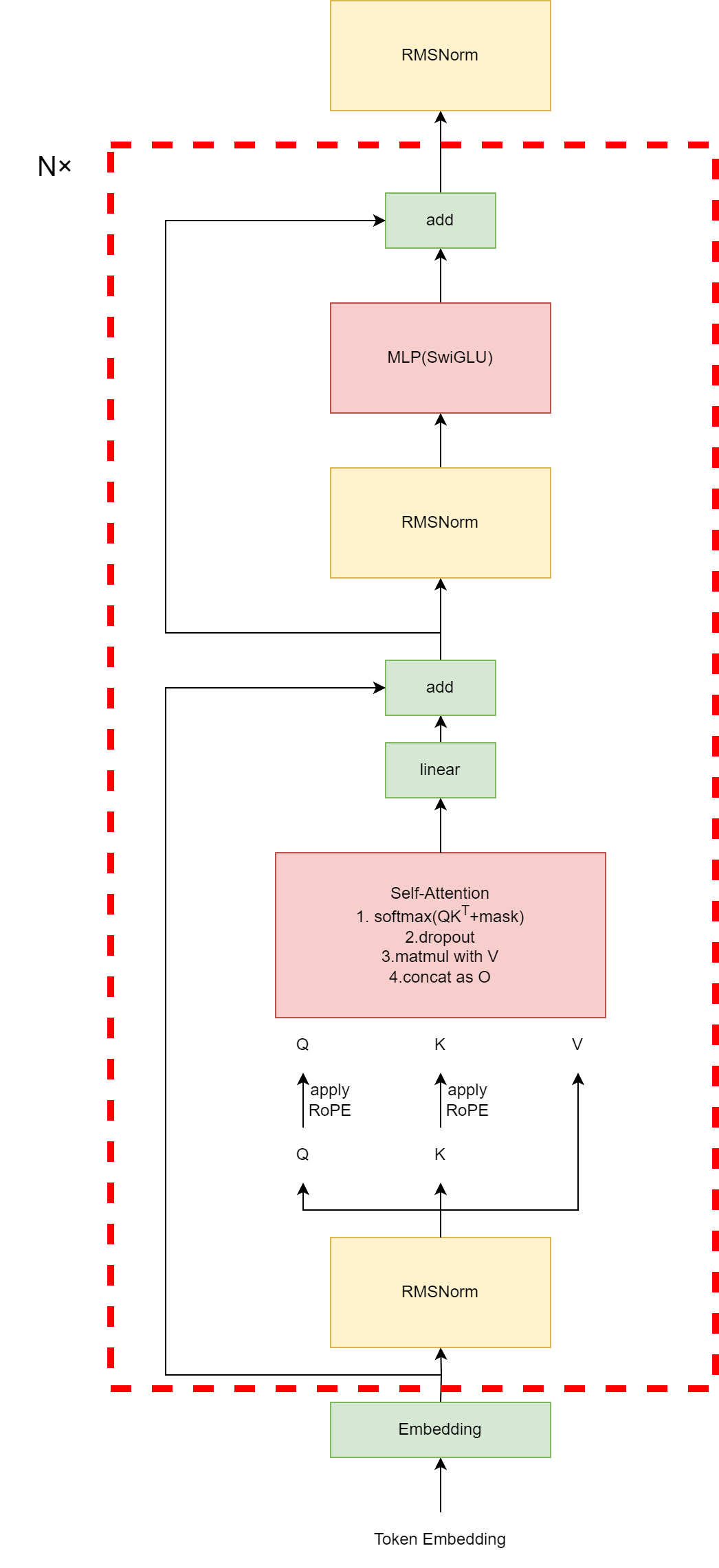
llama1

论文中说，该模型与Vanilla Transformer有三处区别：

  1. Pre-normalization and RMSNorm

    image-20240904222219836

    ​ 原始Transformer中使用post-norm居多，后来使用pre-norm居多，而且往往在FFN之前也加一个norm。尤其在大模型中，可能在通过LN之后MHA之前，Q和K还要加上旋转位置编码。

    参考：【重新了解Transformer模型系列_1】PostNorm/PreNorm的差别

  2. SwiGLU activation function

    SwiGLU激活函数不太像传统的ReLU等激活函数那样简单，比如ReLU都不带参数，而SwiGLU乍一看上去不明觉厉，实际上将SwiGLU理解成对传统FFM的替换，感觉更合适一些。直接看公式有点懵，看图更容易理解，下面是FFM和SwiGLU的对比

    SwiGLU

    SwiGLU写成公式就是 S w i G L U ( x ) = [ S i G U ( g a t e _ p r o j ( x ) ) ⊙ u p _ p r o j ( x ) ] × d o w n _ p r o j ( x ) SwiGLU(x) = \left [ SiGU \left( gate\_proj(x) \right) \odot up\_proj(x) \right] \times down\_proj(x) SwiGLU(x)=[SiGU(gate_proj(x))⊙up_proj(x)]×down_proj(x)，其中可能有点困惑的是这个 8 h 3 \frac{8h}{3} 38h​是怎么来的，实际上就是为了左右这两个结构的参数量相等： 2 × h × 4 h ≡ 2 × h × 8 h 3 + 8 h 3 × h 2 \times h \times 4h \equiv 2 \times h \times \frac{8h}{3} + \frac{8h}{3} \times h 2×h×4h≡2×h×38h​+38h​×h

  3. Rotary Embedding

下面是模型配置，验证一下前面推出来的参数量相关的公式能否对上：

paramshlabVintermediate_sizecalculated params= 2 V h + ( 12 h 2 + 13 h ) l 2Vh+(12h^2+13h)l 2Vh+(12h2+13h)l
6.7B409632324M32K110086706298880 ≈ \approx ≈ 6.71B
13.0B512040404M32K1382412913254400 ≈ \approx ≈ 12.91B
32.5B665660524M32K1792032328857600 ≈ \approx ≈ 32.33B
65.2B819280644M32K2201664957317120 ≈ \approx ≈ 64.96B

每次总是差一点，但是差的不多，差在了哪里呢？MLP部分，理论上intermediate_size= 8 h 3 \frac{8h}{3} 38h​，但是实际上可能会比这个值大一些，往往向上取到256、512、1024等的倍数，对矩阵乘法性能更好，因此来修正一下参数量、计算量、激活值的量化分析：

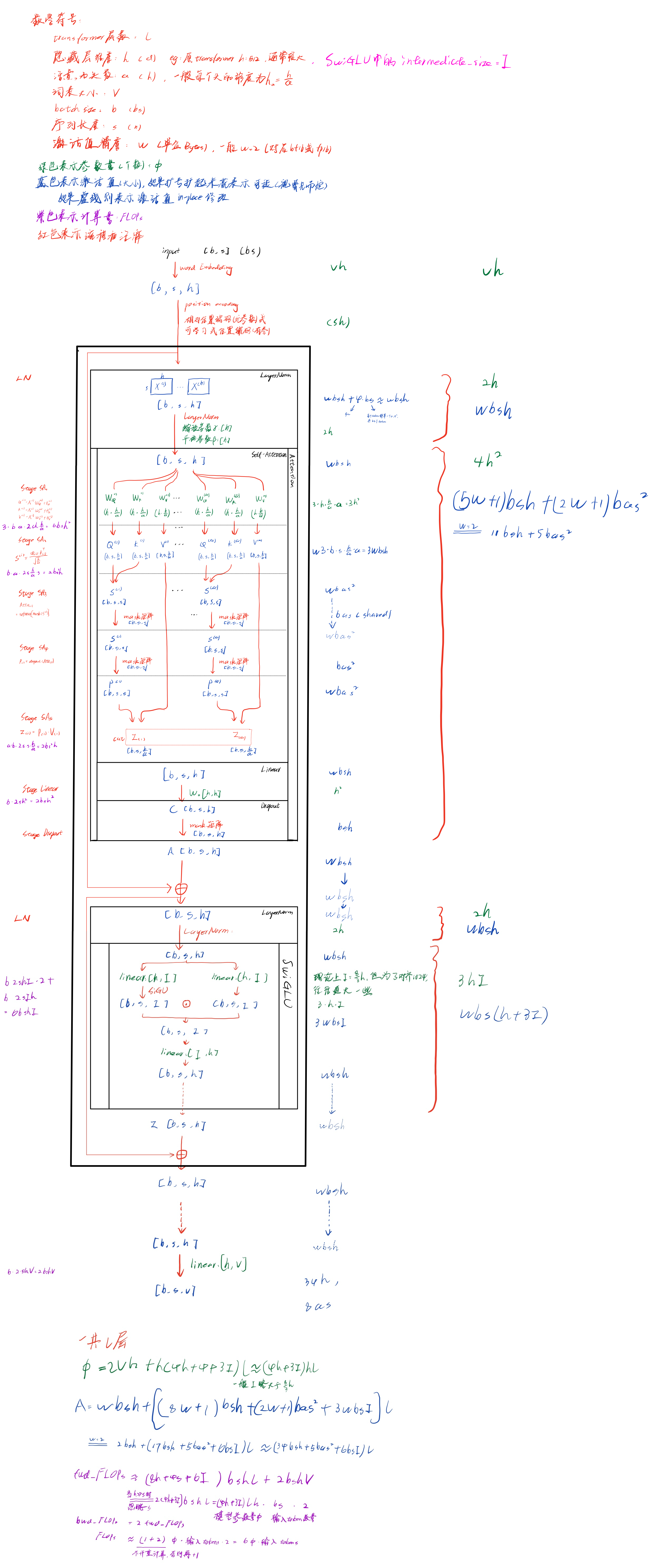
transformer详细分析(llama)

重新计算一下，这次参数量就很接近了

paramshlabVintermediate_sizecalculated params= 2 V h + ( 4 h + 4 + 3 I ) h l 2Vh+(4h+4+3I)hl 2Vh+(4h+4+3I)hl
6.7B409632324M32K110086738673664 ≈ \approx ≈ 6.74B
13.0B512040404M32K1382413016268800 ≈ \approx ≈ 13.02B
32.5B665660524M32K1792032529735680 ≈ \approx ≈ 32.53B
65.2B819280644M32K2201665286963200 ≈ \approx ≈ 65.29B
Llama 2: Llama 2: Open Foundation and Fine-Tuned Chat Models

Llama2在模型结构方面与Llama1相差不大，只是将MHA替换为GQA，将attention的context length从2k提升到4k。下面是Llama2的模型配置

confighlabVintermediate_sizeMHA or GQAcalculated params= 2 V h + ( 12 h 2 + 13 h ) l 2Vh+(12h^2+13h)l 2Vh+(12h2+13h)lcalculated params= 2 V h + ( 4 h + 4 + 3 I ) h l 2Vh+(4h+4+3I)hl 2Vh+(4h+4+3I)hl
7B, config409632324M32K11008MHA6706298880 ≈ \approx ≈ 6.71B6738673664 ≈ \approx ≈ 6.74B
13B, config512040404M32K13824MHA12913254400 ≈ \approx ≈ 12.91B13016268800 ≈ \approx ≈ 13.02B

至于70B的config（h=8192, l=80, a=64, b=4M, V=32K, intermediate_size=28672, g=8）使用了group=8的GQA，只有attention部分的参数量会发生一些变化，调整公式后，分别计算一下：

  • calculated params= 2 V h + [ 10 h 2 + 11 h + 2 g a ( h 2 + h ) ] l 2Vh+\left[ 10h^2 + 11h + \frac{2g}{a}(h^2+h)\right] l 2Vh+[10h2+11h+a2g​(h2+h)]l = 5556092928 ≈ \approx ≈ 55.56B，相差较大
  • llama calculated params= 2 V h + [ ( 2 + 2 g a ) h 2 + 4 h + 3 h I ] l 2Vh + \left [ (2+\frac{2g}{a}) h ^ 2 + 4h + 3hI \right ] l 2Vh+[(2+a2g​)h2+4h+3hI]l = 68977950720 ≈ \approx ≈ 68.98B，比较接近了

因此，对于transformer而言，

  • 如果MLP是传统FFN那样的结构，calculated params= 2 V h + ( 12 h 2 + 13 h ) l 2Vh+(12h^2+13h)l 2Vh+(12h2+13h)l
    • 如果attention部分使用了GQA，则calculated params= 2 V h + [ 10 h 2 + 11 h + 2 g a ( h 2 + h ) ] l 2Vh+\left[ 10h^2 + 11h + \frac{2g}{a}(h^2+h)\right] l 2Vh+[10h2+11h+a2g​(h2+h)]l
  • 如果MLP是SwiGLU那样的结构，calculated params= 2 V h + ( 4 h + 4 + 3 I ) h l 2Vh+(4h+4+3I)hl 2Vh+(4h+4+3I)hl
    • 如果attention部分使用了GQA，则calculated params= 2 V h + [ ( 2 + 2 g a ) h 2 + 4 h + 3 h I ] l 2Vh + \left [ (2+\frac{2g}{a}) h ^ 2 + 4h + 3hI \right ] l 2Vh+[(2+a2g​)h2+4h+3hI]l

但是总的来说，transformer的复杂度还是 O ( h 2 l ) O(h^2l) O(h2l)级别的

more relative reading：

“Mastering Llama Math (Part-1): A Step-by-Step Guide to Counting Parameters in Llama-2”

LLM - Transformer && LLaMA2 结构分析与 LoRA 详解

Llama 3: The Llama 3 Herd of Models

Llama3的改进相对于Llama2和Llama1，主要体现在使用了更高质量的数据和更大规模的训练，模型结构基本没变。下面是模型配置，

confighlabVintermediate_sizeGQA groupcalculated params= 2 V h + [ ( 2 + 2 g a ) h 2 + 4 h + 3 h I ] l 2Vh + \left [ (2+\frac{2g}{a}) h ^ 2 + 4h + 3hI \right ] l 2Vh+[(2+a2g​)h2+4h+3hI]l
8B, config324096324M->8M->16M128K1433688028422144 ≈ \approx ≈ 8.03B
70B, config808192644M->8M->16M128K28672870550814720 ≈ \approx ≈ 70.55B
405B126163841284M->8M->16M128K532488405849112576 ≈ \approx ≈ 405.85B

参考：

LLaMa-1/2/3 原理+源码——拆解 (KV-Cache, RoPE, RMSNorm, GQA, SwiGLU)

关于激活的分析

前面总说中间激活可能很占显存，我们来分析几个case。

GPT-3

confighlabsV from GPT-2activation ≈ ( 34 b s h + 5 b a s 2 ) l \approx (34bsh+5bas^2)l ≈(34bsh+5bas2)lactivation （with GQA） ≈ [ ( 28 + 4 g a ) b s h + 5 b a s 2 ] l \approx \left [ (28+\frac{4g}{a})bsh+5bas^2\right]l ≈[(28+a4g​)bsh+5bas2]l
GPT-3 Small: 125M7681264120485025715972.0MB ≈ 67.0 × 2 Φ \approx 67.0 \times 2\Phi ≈67.0×2Φ15873.0MB ≈ 66.58 × 2 Φ \approx 66.58 \times 2\Phi ≈66.58×2Φ
GPT-3 Medium: 350M10242464120485025732352.0MB ≈ 48.5 × 2 Φ \approx 48.5 \times 2\Phi ≈48.5×2Φ32088.0 ≈ 48.1 × 2 Φ \approx 48.1 \times 2\Phi ≈48.1×2Φ
GPT-3 Large: 760M15362496120485025748528.0 MB ≈ 33.5 × 2 Φ \approx 33.5 \times 2\Phi ≈33.5×2Φ48120.0MB ≈ 33.2 × 2 Φ \approx 33.2 \times 2\Phi ≈33.2×2Φ
GPT-3 2.7B25603280120485025755.3GB ≈ 11.0 × 2 Φ \approx 11.0 \times 2\Phi ≈11.0×2Φ wrong54.4GB ≈ 10.82 × 2 Φ \approx 10.82 \times 2\Phi ≈10.82×2Φ
GPT-3 6.7B409632128120485025788.5GB ≈ 7.10 × 2 Φ \approx 7.10 \times 2\Phi ≈7.10×2Φ87.1GB ≈ 6.98 × 2 Φ \approx 6.98 \times 2\Phi ≈6.98×2Φ
GPT-3 13B5140401281204850257113.3GB ≈ 4.68 × 2 Φ \approx 4.68 \times 2\Phi ≈4.68×2Φ111.1GB ≈ 4.59 × 2 Φ \approx 4.59 \times 2\Phi ≈4.59×2Φ
GPT-3 175B12288961281204850257316.5GB ≈ 0.97 × 2 Φ \approx 0.97 \times 2\Phi ≈0.97×2Φ303.6GB ≈ 0.93 × 2 Φ \approx 0.93 \times 2\Phi ≈0.93×2Φ
GPT-3 175B122889612882048502572532.0GB ≈ 7.77 × 2 Φ \approx 7.77 \times 2\Phi ≈7.77×2Φ2428.5GB ≈ 7.45 × 2 Φ \approx 7.45 \times 2\Phi ≈7.45×2Φ
GPT-3 175B12288961286420485025719.78TB ≈ 62.14 × 2 Φ \approx 62.14 \times 2\Phi ≈62.14×2Φ18.97TB ≈ 59.60 × 2 Φ \approx 59.60 \times 2 \Phi ≈59.60×2Φ

Llama-2：

confighlabsVintermediate_sizeGQA: groupactivation （with GQA） ≈ [ ( 13 + 4 g a ) b s h + 5 b a s 2 + 6 b s I ] l \approx \left [ (13+\frac{4g}{a})bsh+5bas^2 + 6bsI\right]l ≈[(13+a4g​)bsh+5bas2+6bsI]l
7B, config409632321409632K1100832(MHA)96.6GB ≈ 7.4 × 2 Φ \approx 7.4 \times 2\Phi ≈7.4×2Φ
13B, config512040401409632K1382440(MHA)150.9GB ≈ 6.2 × 2 Φ \approx 6.2 \times 2\Phi ≈6.2×2Φ
70B, config819280641409632K286728486.25GB ≈ 3.7 × 2 Φ \approx 3.7 \times 2\Phi ≈3.7×2Φ
70B, config819280648409632K2867283890.0GB ≈ 29.8 × 2 Φ \approx 29.8 \times 2\Phi ≈29.8×2Φ
70B, config8192806464409632K28672830.39TB ≈ 238.7 × 2 Φ \approx 238.7 \times 2\Phi ≈238.7×2Φ

由于前面分析过，intermediate_size往往会略微大于 8 h 3 \frac{8h}{3} 38h​，因此根据前面分析的llama结构，重新推导一下激活的计算公式，这里省略了。

可以看出，当大batch、长序列的情况下，中间激活可以是模型参数所占显存的很多倍，即使使用了GQA。

上面都是在训练场景下的激活值分析，在推理阶段中，可以使用kv-cache减少模型计算量，同时中间激活也大幅度减少，kv-cache的大小为 2 w k v b s m h 2w_{kv}bs_mh 2wkv​bsm​h（单层），我们也来量化分析一下（假设 w k v w_{kv} wkv​=2，且s=1，推理context长度最后一个token的情况，即最坏情况）

configb s m s_m sm​halkv_cache size= 2 w k v b s m h l 2w_{kv}bs_mhl 2wkv​bsm​hlwithout kv-cache activation ≈ ( 34 b s m h + 5 b a s m 2 ) l \approx (34bs_mh+5bas_m^2)l ≈(34bsm​h+5basm2​)lwith kv-cache activation ≈ ( 30 b h + 4 b s m h + 5 b a s m ) l \approx (30bh+4bs_mh+5bas_m)l ≈(30bh+4bsm​h+5basm​)l
GPT-3 Small: 125M12048768641272MB ≈ 0.30 × 2 Φ \approx 0.30 \times 2\Phi ≈0.30×2Φ15972.0MB ≈ 67.0 × 2 Φ \approx 67.0 \times 2\Phi ≈67.0×2Φ79.8MB ≈ 0.33 × 2 Φ \approx 0.33 \times 2\Phi ≈0.33×2Φ
GPT-3 Medium: 350M1204810246424192MB ≈ 0.29 × 2 Φ \approx 0.29 \times 2\Phi ≈0.29×2Φ32352.0MB ≈ 48.5 × 2 Φ \approx 48.5 \times 2\Phi ≈48.5×2Φ207.7MB ≈ 0.31 × 2 Φ \approx 0.31 \times 2\Phi ≈0.31×2Φ
GPT-3 Large: 760M1204815369624288MB ≈ 0.20 × 2 Φ \approx 0.20 \times 2\Phi ≈0.20×2Φ48528.0MB ≈ 33.5 × 2 Φ \approx 33.5 \times 2\Phi ≈33.5×2Φ311.6MB ≈ 0.21 × 2 Φ \approx 0.21 \times 2\Phi ≈0.21×2Φ
GPT-3 2.7B1204825608032640MB ≈ 0.12 × 2 Φ \approx 0.12 \times 2\Phi ≈0.12×2Φ55.3GB ≈ 11.0 × 2 Φ \approx 11.0 \times 2\Phi ≈11.0×2Φ667.3MB ≈ 0.13 × 2 Φ \approx 0.13 \times 2\Phi ≈0.13×2Φ
GPT-3 6.7B120484096128401280MB ≈ 0.1 × 2 Φ \approx 0.1 \times 2\Phi ≈0.1×2Φ110.6GB ≈ 8.9 × 2 Φ \approx 8.9 \times 2 \Phi ≈8.9×2Φ1334.7MB ≈ 0.1 × 2 Φ \approx 0.1 \times 2 \Phi ≈0.1×2Φ
GPT-3 13B120485140128963.76GB ≈ 0.15 × 2 Φ \approx 0.15 \times 2\Phi ≈0.15×2Φ272.0GB ≈ 11.2 × 2 Φ \approx 11.2 \times 2\Phi ≈11.2×2Φ3.89GB ≈ 0.16 × 2 Φ \approx 0.16 \times 2\Phi ≈0.16×2Φ
GPT-3 175B1204812288128969.0GB ≈ 0.02 × 2 Φ \approx 0.02 \times 2\Phi ≈0.02×2Φ316.5GB $\approx 0.97\times 2\Phi $9.15GB ≈ 0.03 × 2 Φ \approx 0.03 \times 2\Phi ≈0.03×2Φ
GPT-3 175B82048122881289672.0GB ≈ 0.22 × 2 Φ \approx 0.22 \times 2\Phi ≈0.22×2Φ2532.0GB ≈ 7.77 × 2 Φ \approx 7.77 \times 2\Phi ≈7.77×2Φ73.2GB ≈ 0.22 × 2 Φ \approx 0.22 \times 2\Phi ≈0.22×2Φ
GPT-3 175B6420481228812896576.0GB ≈ 1.77 × 2 Φ \approx 1.77 \times 2\Phi ≈1.77×2Φ19.78TB ≈ 62.1 × 2 Φ \approx 62.1 \times 2\Phi ≈62.1×2Φ585.6GB ≈ 1.80 × 2 Φ \approx 1.80 \times 2\Phi ≈1.80×2Φ

可以看出在推理时，kv-cache大幅度减少了中间激活。而且使用了kv-cache以后，kv-cache在激活中占据了绝大部分的比例，kv-cache甚至可以超过模型所占内存。

关于计算量的分析

量化分析模型的计算量，主要是为了预估模型训练时间。根据前面的分析，一个FWD+BWD的iteration训练过程中，计算量FLOPs= 6 × Φ × 输入 t o k e n s 数量 6 \times \Phi \times 输入tokens数量 6×Φ×输入tokens数量，因此可以大致估计训练时间= 6 × Φ × 输入 t o k e n s 数量 G P U 数量 × G P U 算力 ( f l o p s ) × M F U \frac{6 \times \Phi \times 输入tokens数量}{GPU数量\times GPU算力(flops) \times MFU} GPU数量×GPU算力(flops)×MFU6×Φ×输入tokens数量​。

其他说明

1. LayerNorm的计算

LayerNorm的计算过程见pytorch LayerNorm参数详解，计算过程，总结一下就是：

  1. 比如输入是[b,s,h]，LN的normalized_shape=[h]，此时就是对每一个大小为h的向量分别进行归一化（一共b*s个）
  2. 然后如果LN的elementwise_affine=True，就需要对每个大小为h的向量elementwise的乘上 γ : [ h ] \gamma: [h] γ:[h]，再elementwise的加上 β : [ h ] \beta:[h] β:[h]， γ \gamma γ和 β \beta β就是该LN层的两个可学习的参数。如果LN的elementwise_affine=False，则只会进行第一步的归一化，不会进行第二步的affine

一个有趣的问题是，Transformer中的LayerNorm可以并行吗？

关键词： Welford online Algorithm，当一个集合新增加一个元素 x N x_N xN​的时候，可以通过前N-1个样本的corrected sum of squares( ∑ i = 1 N − 1 ( x i − x ˉ ) 2 \sum_{i=1}^{N-1}(x_i-\bar{x})^2 ∑i=1N−1​(xi​−xˉ)2)，计算出前N个样本的corrected sum of squares，从而只需要one pass就可以完成LN的计算（之前navie的方法是two pass）

2. 关于dropout的位置

一共（可能）在有四个地方有dropout：

  1. 在PositionalEmbedding中有一个dropout：dropout(x + PositionEmbedding(x))，不过好像LLM现在使用旋转位置编码RoPE多一些，在计算attention之前在Q和K上加上RoPE，一开始输入的embedding不加PositionalEmbedding了
  2. 在softmax计算得到的attention score之后有一个droput： d r o p o u t ( s o f t m a x ( Q K T s c a l e + c a s u a l _ m a s k ) ) dropout( softmax(\frac{QK^T}{scale}+casual\_mask) ) dropout(softmax(scaleQKT​+casual_mask))
  3. 在sublayer（Attention和MLP）计算完之后，各有一个dropout：x+dropout(sublayer(norm(x)))

总结

transformer的参数量的复杂度是 O ( h 2 l ) O(h^2l) O(h2l)级别的，粗略估计可以认为是 12 h 2 l 12h^2l 12h2l或者 ( 4 h + 3 I ) h l (4h+3I)hl (4h+3I)hl，如果要详细分析，就要看一看每个部分的结构，是否使用了bias，使用的不同优化，比如：

  • 如果MLP是传统FFN那样的结构，calculated params= 2 V h + ( 12 h 2 + 13 h ) l 2Vh+(12h^2+13h)l 2Vh+(12h2+13h)l
    • 如果attention部分使用了GQA，则calculated params= 2 V h + [ 10 h 2 + 11 h + 2 g a ( h 2 + h ) ] l 2Vh+\left[ 10h^2 + 11h + \frac{2g}{a}(h^2+h)\right] l 2Vh+[10h2+11h+a2g​(h2+h)]l
  • 如果MLP是SwiGLU那样的结构，calculated params= 2 V h + ( 4 h + 4 + 3 I ) h l 2Vh+(4h+4+3I)hl 2Vh+(4h+4+3I)hl
    • 如果attention部分使用了GQA，则calculated params= 2 V h + [ ( 2 + 2 g a ) h 2 + 4 h + 3 h I ] l 2Vh + \left [ (2+\frac{2g}{a}) h ^ 2 + 4h + 3hI \right ] l 2Vh+[(2+a2g​)h2+4h+3hI]l

对transformer中间激活的分析要分训练场景和推理场景

  • 在训练场景中，中间激活可以是模型参数所占显存的很多倍，尤其在大batch、长序列的情况下。
    • 中间激活值所占显存粗略估计可以认为是 ( 34 b s h + 5 b a s 2 ) l (34bsh+5bas^2)l (34bsh+5bas2)l或者 ( 17 b s h + 5 b a s 2 + 6 b s I ) l (17bsh+5bas^2+6bsI)l (17bsh+5bas2+6bsI)l，可以看出与输入token数量（batch和seq_len）、隐藏层维度、头数、intermediate_size、层数相关，因此相对参数量的分析稍微复杂一点。
  • 在推理场景中，prefill阶段基本同训练场景，decode阶段每次输入的序列长度为1，而且默认使用kv-cache。由于使用kv-cache，中间激活相对于训练时的中间激活大幅度减小，但是在大batch、长序列的情况下，kv-cache的显存占用仍然可能超过模型参数的显存占用。还有一点需要注意，推理场景中kv-cache在中间激活中占据了绝大部分。
    • 中间激活值所占显存粗略估计可以认为是 ( 30 b h + 4 b s m h + 5 b a s m ) l (30bh+4bs_mh+5bas_m)l (30bh+4bsm​h+5basm​)l或者 ( 13 b h + 4 b s m h + 5 b s m a + 6 b I ) l (13bh+4bs_mh+5bs_ma+6bI)l (13bh+4bsm​h+5bsm​a+6bI)l

对transformer的计算量的分析比较简单，transformer中计算较为规整，计算量体现在若干个大块矩阵的乘法。一般量化分析计算量主要是为了预估模型训练时间，所以一般分析的不多（一般也没有机会训练大模型，如果训练普通规模的网络，尝试跑几个iteration就能估计）。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/2121533.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

使用 nuxi upgrade 升级现有nuxt项目版本

使用 nuxi upgrade 升级现有nuxt项目版本

title: 使用 nuxi upgrade 升级现有nuxt项目版本 date: 2024/9/10 updated: 2024/9/10 author: cmdragon excerpt: 摘要：本文介绍了如何使用nuxi upgrade命令升级Nuxt 3项目，包括打开终端、运行升级命令、使用选项、测试项目等步骤，以及升级前的注意事项，如备份代码、检…
阅读更多...
shader 案例学习笔记之绘制圆

shader 案例学习笔记之绘制圆

环境搭建：参考glsl vscode环境搭建 先上代码 #ifdef GL_ES precision mediump float; #endifuniform vec2 u_resolution;void main(){vec2 st gl_FragCoord.xy/u_resolution.xy;st - 0.5;st.x * u_resolution.x/u_resolution.y;float r length(st);float d ste…
阅读更多...
【面试分享】面试题——网络题目_网络面试题

【面试分享】面试题——网络题目_网络面试题

🤟 基于入门网络安全/黑客打造的：👉黑客&网络安全入门&进阶学习资源包 一、题目 1、网关、网桥、路由器、中继器作用、实现以及对应的osi层? 2、MAC地址是什么? 3、webSocket是什么? 4、常见的协议有哪些？ 5、什么…
阅读更多...
交换机vlan配置实现

交换机vlan配置实现

交换机配置 1. 配置交换机速度 进入交换机相应端口。 speed数值： 单位为Mbits;可选10，100，auto duplex参数：参数可选full全双工,half半双工,auto自适应 配置交换机管理IP地址： 在全局模式下： interf…
阅读更多...
Qt使用UDP进行单波通信

Qt使用UDP进行单波通信

Qt使用UDP进行单波通信 我们一般学习完基础的一些编程之后就会开始接触网络编程，我们熟悉的网络编程一般会涉及到两个协议一个时TCP，一个是UDP。TCP一般是point to point，UDP一般有单播和广播两种方式，那么我们今天就来学习一下单…
阅读更多...
ECRS软件作业分析：提升工厂生产效率的钥匙

ECRS软件作业分析：提升工厂生产效率的钥匙

在竞争日益激烈的现代工业环境中，如何提升生产效率、降低资源消耗、增加产品价值，成为了每一家制造企业必须面对的重要课题。作业分析，作为一种科学的管理工具，正逐步成为企业优化生产流程、提升竞争力的关键手段。本文旨在深入探…
阅读更多...
Unity SRP 可编程渲染管线的基本用法

Unity SRP 可编程渲染管线的基本用法

可编程渲染管线使用教程 SRP 可以处理Canvas为Screen Space - Overlay的渲染 安装插件 首先进入package manager，下载Core RP Lib组件 创建渲染管线 编写渲染管线逻辑脚本 新建脚本取名为MPipeLine，该脚本用于实现渲染管线的处理逻辑 using Unity…
阅读更多...
Python计算机视觉 第7章-图像搜索

Python计算机视觉 第7章-图像搜索

Python计算机视觉 第7章-图像搜索 7.1　基于内容的图像检索 在大型图像数据库上，CBIR（Content-Based Image Retrieval，基于内容的图像检索）技术用于检索在视觉上具相似性的图像。这样返回的图像可以是颜色相似、纹理相似、图像中…
阅读更多...
优秀一点点

优秀一点点

在职场中，想要获得晋升，重要的是比其他同事优秀一点点。这就好比百米短跑比赛，第一名比第二名可能之快了0.01秒，这个0.01秒，和跑一百米所花的10秒钟比起来，可能只有千分之一。也就是说，第一名比…
阅读更多...
麦汁煮沸工艺

麦汁煮沸工艺

麦汁煮沸是啤酒酿造中至关重要的工艺环节之一，直接影响啤酒的风味。今天，天泰邀您一起深入探讨这一关键的酿造技术。 煮沸麦汁 在煮沸麦汁时，时间和温度控制至关重要。通常，麦汁煮沸持续 40 到 50 分钟，具体时间取决于…
阅读更多...
OpenAI Embeddings API: How embeddings work?

OpenAI Embeddings API: How embeddings work?

题意：OpenAI 嵌入 API：嵌入是如何工作的？ 问题背景： There are quite a few tutorials on embeddings in OpenAI. I cant understand how they work. 在OpenAI中有很多关于嵌入的教程，但我无法理解它们是如何工作的。…
阅读更多...
轻松实现游戏串流,内网穿透

轻松实现游戏串流,内网穿透

一、部署Gemini Gemini使用教程 二、部署Moonlight 过程大概说一下，网上有太多太多moonlight的东西了 需要运行游戏的机器上安装GFE（GeForce Experience），登录并开启GAMESTREAM（游戏串流）功能 注&…
阅读更多...
什么是 Flash Attention

什么是 Flash Attention

Flash Attention 是 由 Tri Dao 和 Dan Fu 等人在2022年的论文 FlashAttention: Fast and Memory-Efficient Exact Attention with IO-Awareness 中 提出的， 论文可以从 https://arxiv.org/abs/2205.14135 页面下载，点击 View PDF 就可以下载。 下面我…
阅读更多...
Php数组函数中的那些什么sort排序函数是不是很乱? 可以这样看。以及php搜索给定的值在数组中最后一次出现的位置的实现思考

Php数组函数中的那些什么sort排序函数是不是很乱? 可以这样看。以及php搜索给定的值在数组中最后一次出现的位置的实现思考

一、Php数组函数中的那些什么sort排序函数是不是很乱? 可以这样看 PHP的数组函数真不少，甚至对一个程序员来说，在其整个程序生涯中有些方法他永远也不会用上。不过每一个方法都有其价值、或者在出现的时候有其价值。所以偶尔有空时还是可以去看看。在这…
阅读更多...
并发编程：线程池（下）

并发编程：线程池（下）

一、线程池常用的阻塞队列有哪些？ 新任务来的时候会先判断当前运行的线程数量是否达到核心线程数，如果达到的话，新任务就会被存放在队列中。 不同的线程池会选用不同的阻塞队列，我们可以结合内置线程池来分析。 容量为 Integer…
阅读更多...
UE5 半透明阴影 快速解决方案

UE5 半透明阴影 快速解决方案

Step 1： 打开该选项 Step 2： 将半透明材质给到模型后，设置光照的Shadow Resolution Scale，越大，阴影的效果越好 Step 3： 用这种方式去做，阴影会因为半透明的程度，降低阴影的浓度 要…
阅读更多...
Spring security 动态权限管理(基于数据库)

Spring security 动态权限管理(基于数据库)

一、简介 如果对该篇文章不了解，请移步上一篇文章：spring security 中的授权使用-CSDN博客 当我们配置的 URL 拦截规则请求 URL 所需要的权限都是通过代码来配置的，这样就比较死板，如果想要调整访问某一个 URL 所需要的权限&…
阅读更多...
【专项刷题】— 队列

【专项刷题】— 队列

1、N 叉树的层序遍历 - 力扣&#xff08;LeetCode&#xff09; 思路&#xff1a; 每次遍历一层节点的时候就把当前节点的值添加到列表中再将当前层的节点的子节点添加到队列中每次遍历完一层之后就添加到总表中代码&#xff1a; public List<List<Integer>> levelO…
阅读更多...
如何远程实时监控员工的电脑屏幕？远程桌面监控的五个可实现方法分享

如何远程实时监控员工的电脑屏幕？远程桌面监控的五个可实现方法分享

想象一下&#xff0c;你在办公室喝着咖啡&#xff0c;员工的电脑屏幕却在数百公里之外实时呈现在你的眼前。你可以看到他们在干什么&#xff0c;是埋头工作还是悄悄摸鱼&#xff1f;远程桌面监控让这一切变得触手可及&#xff0c;简直像给了管理者一双“千里眼”&#xff01; 如…
阅读更多...
RedisTemplate操作String的API

RedisTemplate操作String的API

文章目录 1 String 介绍2 命令3 对应 RedisTemplate API❄️❄️ 3.1 添加缓存❄️❄️ 3.2 设置过期时间(单独设置)❄️❄️ 3.3 获取缓存值❄️❄️ 3.4 删除key❄️❄️ 3.5 顺序递增❄️❄️ 3.6 顺序递减 ⛄4 以下是一些常用的API⛄5 应用场景 1 String 介绍 String 类型…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023