Flash Attention 是 由 Tri Dao 和 Dan Fu 等人在2022年的论文 FlashAttention: Fast and Memory-Efficient Exact Attention with IO-Awareness 中 提出的,
论文可以从 https://arxiv.org/abs/2205.14135 页面下载,点击 View PDF 就可以下载。
下面我们通过详细解读这篇论文,来说明什么是Flash Attention。
Transformer在处理长序列时速度慢且占用大量内存,因为自注意力的时间和内存复杂度与序列长度的平方成正比。近似注意力方法尝试通过牺牲模型质量来减少计算复杂度来解决这个问题,但往往不能实现实际速度提升。我们认为一个缺失的原则是使注意力算法具有IO感知能力——考虑GPU内存层级之间的读取和写入。我们提出了FlashAttention,这是一种IO感知的精确注意力算法,使用平铺技术来减少GPU高带宽内存(HBM)和GPU片上静态随机存储器(SRAM)之间的内存读写次数。我们分析了FlashAttention的IO复杂度,表明它需要比标准注意力更少的HBM访问,并且在一定范围内的SRAM大小下是最优的。FlashAttention训练Transformer比现有基准更快:与MLPerf 1.1训练速度记录相比,BERT-large(序列长度为512)的端到端墙钟速度提高了15%,GPT-2(序列长度为1K)的速度提高了3倍,长距离竞技场(序列长度为1K-4K)的速度提高了2.4倍。

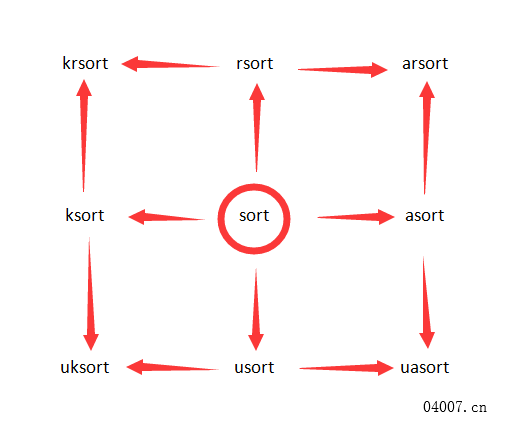
左图:FlashAttention使用平铺技术,防止在(相对)较慢的GPU HBM上生成大型的𝑁×𝑁注意力矩阵(虚线框)。在外部循环(红色箭头)中,FlashAttention循环遍历K和V矩阵的块,并将它们加载到快速的片上静态随机存储器(SRAM)中。在每个块中,FlashAttention循环遍历Q矩阵的块(蓝色箭头),将它们加载到SRAM,并将注意力计算的输出写回HBM。右图:与GPT-2上注意力的PyTorch实现相比的加速效果。FlashAttention不会将大型的𝑁×𝑁注意力矩阵读取和写入HBM,从而使注意力计算加速了7.6倍。
在现代GPU上,计算速度已经超过了内存读取速度,而Transformer中的大多数操作都受到内存访问的限制。对于类似受内存限制的操作,IO感知算法对于读取和写入数据可能占据运行时较大部分的情况至关重要,比如数据库连接、图像处理、数值线性代数等等。然而,诸如PyTorch和Tensorflow等常见的Python深度学习接口并不允许对内存访问进行精细控制。
我们提出了FlashAttention,这是一种新的注意力机制算法,可以在极少的内存访问次数下计算精确的注意力。我们的主要目标是避免从高带宽存储器(HBM)读取和写入注意力矩阵。这需要 (i) 在没有访问整个输入的情况下计算softmax归一化 (ii) 在反向传播过程中不存储大型的中间注意力矩阵。我们应用了两种成熟的技术来解决这些挑战。 (i) 我们重新构造了注意力计算,将输入分成块,并对输入块进行多次遍历,逐步执行softmax归一化(也称为平铺)。 (ii) 我们在正向传播过程中存储了softmax归一化因子,以便在反向传播过程中快速重新计算注意力,这比从HBM读取中间注意力矩阵的标准方法更快。我们在CUDA中实现了FlashAttention,以实现对内存访问的精细控制,并将所有的注意力操作融合到一个GPU核函数中。即使由于重新计算而增加了浮点运算次数,我们的算法在运行时比标准注意力更快,并且使用的内存量(与序列长度成正比)更少,这得益于大大减少的HBM访问量。
我们分析了FlashAttention的IO复杂度,证明它需要𝑂(𝑁^2𝑑^2/𝑀)次HBM访问,其中𝑑是头部维度,𝑀是SRAM的大小,而标准注意力的HBM访问次数为Ω(𝑁𝑑 + 𝑁^2)。对于𝑑和𝑀的典型值,我们证明FlashAttention相比标准注意力需要更少的HBM访问次数。此外,我们提供了一个下界,表明没有精确的注意力算法能够在所有SRAM大小上渐近地改进HBM访问次数。
GPU内存层次结构。GPU内存层次结构包括多种不同大小和速度的内存,较小的内存速度更快。以A100 GPU为例,其具有40-80GB的高带宽存储器(HBM),带宽为1.5-2.0TB/s,每个108个流多处理器具有192KB的片上静态随机存储器(SRAM),其带宽估计约为19TB/s。片上SRAM的速度比HBM快一个数量级,但在尺寸上小几个数量级。随着计算相对内存速度变得更快,操作越来越受到内存(HBM)访问的限制。因此,利用快速的SRAM变得更加重要。
执行模型。GPU拥有大量线程来执行操作(称为核函数)。每个核函数从HBM加载输入到寄存器和SRAM,进行计算,然后将输出写入HBM。
性能特征。根据计算和内存访问的平衡,操作可以被归类为计算受限或内存受限。这通常由算术密集度来衡量,即每个内存访问的算术操作数。
计算受限:操作所需时间取决于算术操作的数量,而在HBM上的访问时间要小得多。典型的例子包括具有大内部维度的矩阵乘法和具有大通道数量的卷积。
内存受限:操作所需时间取决于内存访问次数,而计算所需时间要小得多。例如,大多数其他操作:逐元素(例如,激活,丢弃)和缩减(例如,求和,softmax,批标准化,层标准化)。
核函数融合。加速内存受限操作的最常见方法是核函数融合:如果有多个操作应用于相同的输入,那么可以一次从HBM加载输入,而不是每个操作都进行多次加载。编译器可以自动融合许多逐元素操作。
然而,在模型训练的情境中,中间值仍然需要被写入HBM以供反向传播保存,降低了简单核函数融合的效果。
标准注意力实现
给定输入序列 Q、K、V ∈ R^(𝑁 ×𝑑) ,其中 𝑁 是序列长度,𝑑 是头维度,我们希望计算注意力输出 O ∈ R^(𝑁 ×𝑑) : S = QK^T∈ R^(𝑁 ×𝑁) ,P = softmax(S) ∈ R^(𝑁 ×𝑁) ,O = PV ∈ R^(𝑁 ×𝑑) , 其中 softmax 按行应用。 标准的注意力实现会将矩阵 S 和 P 实现在 HBM,这将占用 𝑂(𝑁^2 ) 的内存。 通常 𝑁 远大于 𝑑(例如,对于 GPT2,𝑁 = 1024,𝑑 = 64)。我们在算法 0 中描述了标准的注意力实现。由于一些或大部分操作是内存绑定的(例如 softmax),大量的内存访问会导致较慢的墙钟时间。 这个问题会因为其他应用于注意力矩阵的逐元素操作而变得更加严重,比如应用于 S 的掩码或应用于 P 的 dropout。因此,已经有许多尝试将多个逐元素操作融合在一起,比如将掩码与 softmax 融合在一起。标准注意力实现在序列长度 𝑁 的 HBM 访问方面呈二次增长。
算法 0
标准注意力实现 要求:矩阵 Q、K、V ∈ R^(𝑁 ×𝑑) 在 HBM 中。
1: 从 HBM 中按块加载 Q、K,计算 S = QK>,将 S 写入 HBM。
2: 从 HBM 中读取 S,计算 P = softmax(S),将 P 写入 HBM。
3: 从 HBM 中按块加载 P 和 V,计算 O = PV,将 O 写入 HBM。
4: 返回 O。
下面我们展示如何以更少的 HBM 读/写操作并且在不存储大型中间矩阵的情况下计算精确的注意力。这产生了一种既内存高效又在墙钟时间上更快的注意力算法。
一种具有平铺和重计算的高效注意力算法
给定输入Q、K、V ∈ R 𝑁 ×𝑑 在HBM中,我们的目标是计算注意力输出O ∈ R^(𝑁 ×𝑑) 并将其写入HBM。我们的目标是减少HBM访问的数量(至少是𝑁的平方级别)。我们应用了两种已建立的技术(平铺、重计算)来克服在子二次HBM访问中计算精确注意力的技术挑战。我们在算法1中描述了这一点。其主要思想是我们将输入Q、K、V分成块,从较慢的HBM加载到较快的SRAM,然后针对这些块计算注意力输出。通过在将每个块的输出按正确的归一化因子进行缩放后相加,我们最终得到了正确的结果。
平铺:我们通过块来计算注意力。Softmax将K的列耦合起来,因此我们分解了大型softmax并进行了缩放。为了数值稳定性,向量𝑥 ∈ R^𝐵的softmax计算如下:

对于向量 𝑥(1), 𝑥(2) ∈ R^𝐵,我们可以将拼接向量 𝑥 = [𝑥(1)𝑥(2)] ∈ R^(2𝐵) 的 softmax 分解为:

因此,如果我们跟踪一些额外的统计数据(𝑚(𝑥), ℓ(𝑥)),我们可以逐块计算softmax。因此,我们将输入 Q、K、V 分割成块(算法1第3行),计算softmax值以及额外的统计数据(算法1第10行),然后将结果合并(算法1第12行)。
重新计算。我们的一个目标是不要为反向传播存储𝑂(𝑁^2)个中间值。反向传播通常需要矩阵 S、P ∈ R^𝑁×𝑁 来计算相对于 Q、K、V 的梯度。然而,通过存储输出 O 和 softmax 归一化统计数据 (𝑚, ℓ),我们可以在反向传播中轻松地从 Q、K、V 的块中重新计算注意力矩阵 S 和 P。这可以看作是一种选择性梯度检查点技术。虽然梯度检查点技术被建议用于减少最大所需内存,但所有已知的实现都必须以速度为代价来换取内存。相比之下,即使有更多的浮点操作数,我们的重新计算也能加速反向传播,因为减少了高带宽内存访问。
实施细节:内核融合。分块使我们能够在一个CUDA内核中实现我们的算法,从高带宽内存加载输入,执行所有的计算步骤(矩阵乘法,softmax,可选的掩码和丢弃,矩阵乘法),然后将结果写回到高带宽内存。这避免了重复地从高带宽内存读取和写入输入和输出。