前言

这里完成每日的创作要求，用一下自己看论文整理的LSM-Tree理论

2.1 LSM-Tree 基础理论

LSM Tree 组织

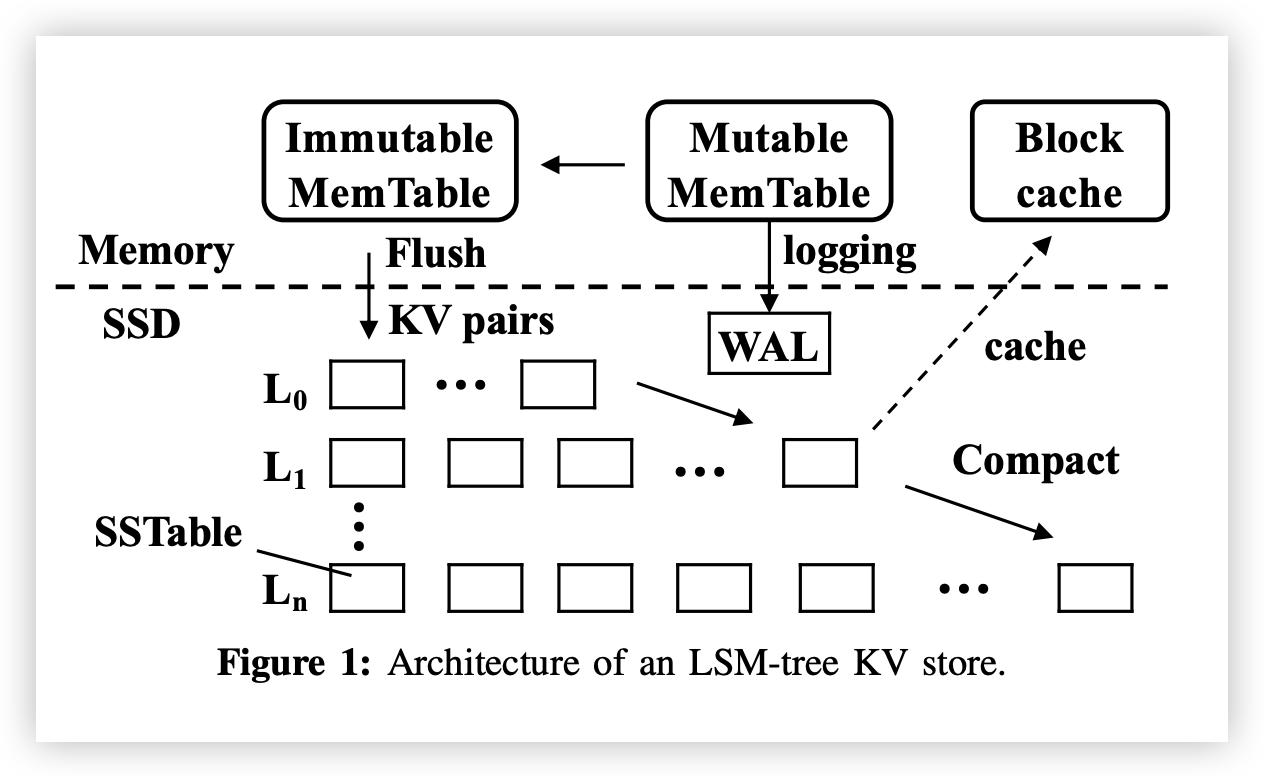
总共有n+1层，代表L0到Ln

每个级别将键值对存储在不可变的固定大小文件中（类似于HDFS的块设定），每个文件有几个 MiB，在持久化存储中被称为SSTables。

每个 SSTable 将 KV 对分组到几个 KiB 大小的数据块中，并保留一个索引块，用于存储 SSTable 中所有数据块的键范围和偏移量（存于SSTable 内部）。
为了实现高效的范围查询，每个 SSTable 按键对所有 KV 对进行排序，并且同一级别（L0 除外）的所有 SSTable 都具有不相交的键范围。此外，Li（2 ≤ i ≤ n）的总大小通常是其较低级别 Li−1 的数倍（例如，RocksDB [16] 中的 10 倍）

Writes

put(key, value) 操作符将一个键值对写入 LSM 树。它首先将键值对附加到预写日志 (WAL) 中，用于崩溃恢复。

然后将键值对写入内存中的可变结构，称为 MemTable。当 MemTable 已满时，它将转换为不可变的 MemTable，该 MemTable 将被刷新并成为磁盘上 L0 中的 SSTable；刷新的键值对也将从 WAL 中删除。SSTables 中的键值对通过压缩迁移到更高级别，步骤如下：

1. 在 Li (0 ≤ i ≤ n − 1) 中选择 SSTable，并在 Li+1 中选择具有重叠键范围的多个 SSTable
2. 合并排序所有键值对并丢弃任何无效（陈旧）的键值对，以及
3. 将活动（非陈旧）键值对作为新 SSTable 写入 Li+1。压缩后，每个级别（L0 除外）的所有键值对都保持排序，因此可以通过二分搜索来查询 Li（i ≥ 1）中的键。请注意，压缩会导致写入放大，因为它会将有效的键值对重写到新的 SSTable 中。

Reads

get(key) 操作符读取给定键的 KV 对并返回其值。它首先搜索当前写入的 MemTable 和内存中的不可变 MemTable，然后从 LSM 树的低级到高级搜索磁盘上的 SSTable。因此**，它会导致读取放大，**因为它经常向不同级别的 SSTable 发出多个随机读取。为了加速读取，每个 SSTable 中的索引块都维护一个布隆过滤器 [6] 来快速检查键是否存在。此外，经常访问的索引块和数据块会缓存在内存中的块缓存中。