最近的一篇来自于Cognitive Sciences的精炼综述带给了我一些对于当下AI的某种反向思考🤔，分享给大家：

这篇综述讨论了如何通过多种降维技术揭示认知科学中的潜在表征空间，并探讨了选择适合研究目标的嵌入算法时需要考虑的关键因素。

文中对如下几个方面进行了论述：

Ⅰ. 认知科学为什么需要多维空间；

Ⅱ. 可观测数据映射到潜在空间产生了什么变化；

Ⅲ. 选择嵌入算法时需要考虑的关键因素；

Ⅵ. 比较和选择嵌入空间；

其中引发我思考🤔的是“Ⅱ”中延展出的：认知或推理过程中所反映出的潜在空间上的动态变化和数据变换模式。（与之前的两篇关于流行空间分布的阐释如出一辙）

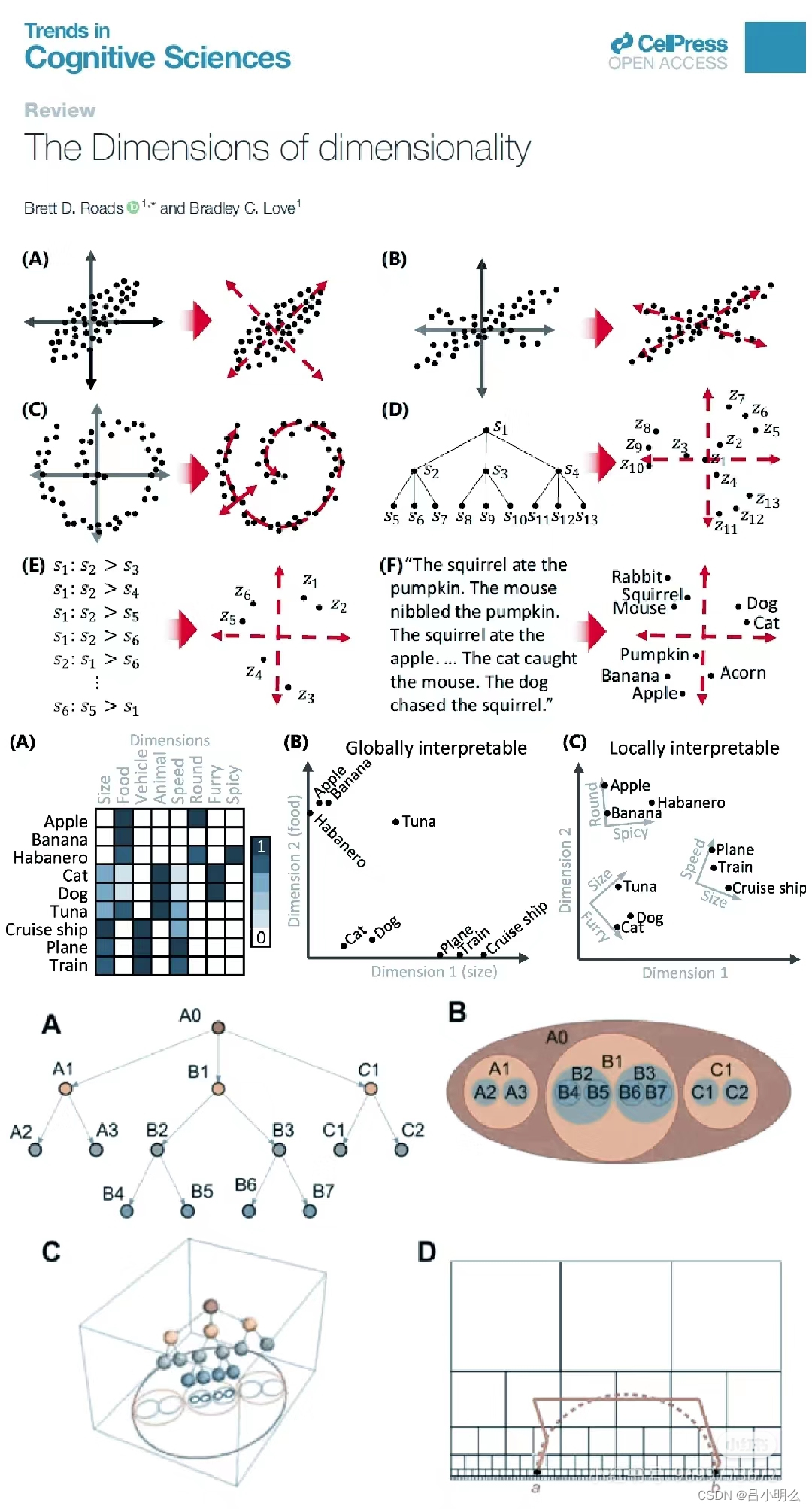
在可观测真实物理空间中，每个维度都与现实中的物理特征紧密相关，这些维度帮助我们理解和测量现实世界中的现象。然而，当我们将这些可观测数据映射到潜在空间时，可以说空间中各维度表征的意义发生了抽象性的变化：

a. 新的潜空间纬度下的表征并不一定对应于我们能够轻易解释的全局性特征（随着不同的任务目标即不同的认知流形势必会有信息损失或语义的熵减）;

b. 这些潜空间维度中所表征的内涵并不一定存在于真实世界中，它们是从输入数据中推断出来的潜变量，存在于理念世界(来自于柏拉图的理想国)；

c.潜空间的动态变化源于真实世界的可想象的客观存在真实变化的抽象或泛化降维，如对于非线性降维后数据的“流形分布”；

可以说，抛开模型结本身与各异的学习机制，适合而完备的潜在维度亦是优秀认知模型的核心要素之一。

那么如何理解和应对“适合的”和“完备的”呢？

我想对于不同的任务目标或不同的认知流形探索过程会对应不同的模式变换方法，如：

① 常见的线性转换方法包括PCA、ICA、傅里叶变换、因子分析和基于张量的降维方法；

② 常用的非线性降维算法包括ISOMAP、t-SNE、UMAP和各种自编码器；其他非线性降维算法还包括核方法、局部线性嵌入、拉普拉斯特征映射、Hessian特征映射和局部切空间对齐；

这里非线性降维算法通常假设数据并非均匀分布，而是分布在较为连续的曲面（即流形）上，如非线性转换（如t-SNE）允许新维度描述一个截然不同的空间，可能在原始空间中扭曲和转动。

而对于当下的llm甚至是未来的AGI来说，可以想象的其通用性所带来的流行空间所覆盖的复杂性及泛化挑战，对于其认知流形的探索或适配模式也许是包罗万象的，我想也是应该遵循于某种scaling law吧。