面向实用的即插即用扩散模型

Paper Title：Towards Practical Plug-and-Play Diffusion Models

Paper是Riiid AI Research发表在CVPR 2023的工作

paper地址

Code地址

Abstract

基于扩散的生成模型在图像生成方面取得了显著的成功。它们的指导公式允许外部模型即插即用地控制各种任务的生成过程，而无需微调扩散模型。然而，直接使用公开的现成模型进行指导会失败，因为它们在噪声输入上的表现不佳。为此，现有的做法是使用被噪声破坏的标记数据对指导模型进行微调。在本文中，我们认为这种做法在两个方面存在局限性：（1）对于单个指导模型来说，处理具有极其多样化噪声的输入太难了；（2）收集标记数据集阻碍了各种任务的扩展。为了解决这些限制，我们提出了一种新策略，该策略利用多位专家，其中每个专家专注于特定的噪声范围并在其相应的时间步指导扩散的逆过程。然而，由于管理多个网络和利用标记数据是不可行的，我们提出了一个称为实用即插即用 (PPAP) 的实用指导框架，它利用参数高效的微调和无数据知识传输。我们详尽地进行了 ImageNet 类条件生成实验，以表明我们的方法可以成功地引导具有较小可训练参数和无标记数据的扩散。最后，我们展示了图像分类器、深度估计器和语义分割模型可以通过我们的框架以即插即用的方式引导公开可用的 GLIDE。

1. Introduction

最近，基于扩散的生成模型 [49] 在各个领域都取得了巨大成功，包括图像生成 [14, 44, 45]、文本转语音 [21, 40] 和文本生成 [32]。具体来说，对于图像生成，最近的研究表明，扩散模型能够生成与 GAN 生成的图像相当的高质量图像 [8,12]，同时不会出现模式崩溃或训练不稳定性 [38]。

除了这些优点之外，它们的公式化还允许外部模型指导 [8, 49, 53]，从而引导扩散模型的生成过程朝着期望的状态发展。由于引导扩散利用了外部指导模型，并且不需要进一步微调扩散模型，因此它具有以即插即用的方式实现廉价且可控生成的潜力。例如，以前的方法使用图像分类器进行类条件图像生成 [8, 53]，使用时尚理解模型进行时尚图像编辑 [28]，使用视觉语言模型进行基于文本的图像生成 [1, 37]。由此可见，如果可以使用公开的现成模型进行指导，就可以轻松地将一种扩散应用于各种生成任务。

为此，一种现有做法是在训练数据集的噪声版本上对外部现成模型进行微调 [8, 12]，以使模型适应在扩散过程中遇到的噪声潜像。然而，我们认为这种做法对即插即用生成有两个挑战：（1）单一指导模型不足以对受不同程度噪声破坏的输入进行预测，即任务太难；（2）它需要标记的训练数据集，这成为利用现成模型的主要障碍。

在本文中，我们首先研究了分类器在不同程度的噪声下的行为，以了解第一个挑战。一方面，在噪声严重的损坏图像上训练的指导模型根据粗糙结构对图像进行分类。因此，这样的模型将指导扩散模型生成必要的骨架特征。同时，在更干净的图像上训练的指导模型会捕捉图像中更精细的细节，指导扩散模型进行最后的润色。

基于这些关键观察，我们提出了一种新颖的多专家策略，该策略使用多个指导模型，每个模型都经过微调以专门针对特定的噪声区域。
尽管多专家策略很有效，但它应该管理多个网络并在将新的现成模型应用于各种生成任务时利用标记数据。

为了更实用地对具有多专家策略的扩散模型进行即插即用指导，我们引入了称为实用即插即用 (PPAP) 的框架。首先，为了防止由于多专家策略导致指导模型的大小过大，我们利用参数高效的微调方案，该方案可以使现成的模型适应嘈杂的图像，同时保留参数数量。其次，我们将现成模型对干净的扩散生成数据的知识转移到专家指导模型，从而无需收集标记数据集。

我们的实证结果证实，我们的方法显著提高了条件图像生成性能，使用现成的模型，这些模型只有少量可训练参数且没有标记数据。我们还展示了公开可用的扩散模型 GLIDE [37] 的各种应用，通过即插即用的方式利用现成的图像分类器、深度估计器和语义分割模型。

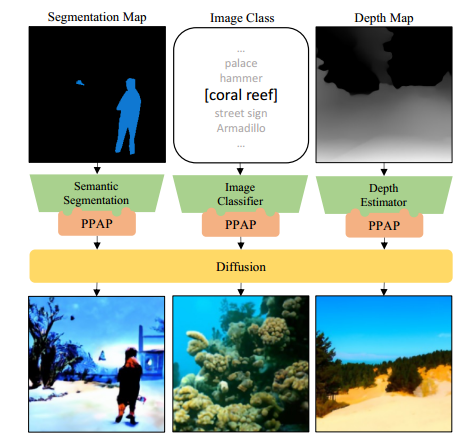
图 1. 我们框架的概览。实用即插即用 (PPAP) 能够利用现成的模型来指导扩散模型。下面显示的图像是通过以即插即用的方式使用 DeepLabV3 [4]、ResNet50 [15] 和 MiDaS [43] 指导无条件 GLIDE [37] 生成的。

2. Related Work

扩散模型 扩散模型 [8, 18, 26, 38, 49] 和基于分数的模型 [51, 53] 属于生成模型，通过逐渐消除噪声从给定分布生成样本。与其他基于可能性的方法（如 VAE [27] 或基于流的模型 [9, 10]）不同，扩散模型已表现出可与 GAN [3, 12, 23] 媲美的卓越生成能力。尽管扩散模型的生成速度较慢，但DDIM [50]、A-DDIM [2]、PNDM [33] 和 DEIS [55] 等先前的研究已显著加快了生成过程。

对于扩散模型中的条件生成，分类器指导 [8, 53] 和无分类器指导 [19] 广泛应用于各种任务 [17,25,29,37,44]。分类器指导使用外部分类器的梯度，而无分类器指导在有标签和无标签的扩散模型的预测之间进行插值。然而，对于无分类器指导，扩散模型应该作为标记数据来学习，因为它需要对标签进行预测。在本文中，我们重点介绍分类器指导，它冻结无条件扩散模型，并指导它与外部模型一起以即插即用的方式进行各种没有标记数据的条件生成。

即插即用生成 沿袭 [36] 的说法，我们使用“即插即用”一词来指代无需联合训练可替换条件网络和生成模型，即可根据可替换条件网络给出的条件在测试时生成图像的能力。在图像生成 [11, 22, 24, 36, 52] 和文本生成 [6, 34, 48] 中，已经出现了各种即插即用条件生成的尝试，通过将约束绑定到非条件模型，例如 GAN [12]、VAE [27]。这些方法允许单个非条件生成模型通过改变约束模型来执行各种任务。

与我们最相似的工作是，Graikos 等人 [13] 尝试通过直接使用现成的模型优化潜在图像，将扩散模型即插即用地用于各种任务。然而，它无法像 ImageNet 那样在复杂分布中生成有意义的图像。与此相反，我们的方法通过在现成的模型中引入小参数并使其适用于潜在图像，成功地在复杂数据集中进行了指导。

3. Motivation

3.1. Preliminaries

---

扩散模型

扩散模型 $[14,44,45,49]$ 是一类生成模型，通过逐渐去噪随机噪声来采样数据。扩散模型包括两个阶段，即正向和反向过程。正向扩散过程 $q$ 逐渐向数据 $x_0\sim q\left(x_0\right)$ 添加噪声，噪声的方差依据某种时间表 ${\beta }_t$，如下所示：

$$q\left(x_t\mid x_{t-1}\right)=\mathcal{N}\left(x_t;\sqrt{1-{\beta }_t}{x}_{t-1},{\beta }_t\mathbf{I}\right)(1)$$

我们重复正向过程，直到达到最大时间步 $T$。给定 $x_0$，我们可以直接采样 $x_t$，公式如下：

$$x_t=\sqrt{{\alpha }_t}{x}_0+\sqrt{1-{\alpha }_t}ϵ,ϵ\sim \mathcal{N}(0,\mathbf{I})(2)$$

其中 ${\alpha }_t:={\prod }_{s=1}\left(1-{\beta }_s\right)$。注意，随着 $t$ 增加，$\sqrt{{\alpha }_t}$ 减小，使得 $\sqrt{{\alpha }_T}\approx 0$。

反向扩散过程从随机噪声 $x_T\sim \mathcal{N}(0,\mathbf{I})$ 开始，逐步生成去噪样本 $x_{T-1},x_{T-2},\dots$，直到达到最终样本 $x_0$。使用噪声预测模型 ${ϵ}_{\theta }\left(x_t,t\right)$，反向过程以 $z\sim \mathcal{N}(0,\mathbf{I})$ 的方式迭代去噪 $x_t$，如下所示：

$$x_{t-1}=\frac{1}{\sqrt{1-{\beta }_t}}\left(x_t-\frac{{\beta }_t}{\sqrt{1-{\alpha }_t}}{ϵ}_{\theta }\left(x_t,t\right)\right)+{\sigma }_{t}z(3)$$

其中 ${\sigma }_t^2$ 是反向过程的方差。

外部模型引导的扩散

引导扩散通过利用外部模型来引导扩散模型的样本生成 $[8,49,53]$。具体来说，假设我们有一个外部引导模型 $f_{\varphi }$，该模型可以预测输入的某些特征，例如，预测图像类别的分类器。在反向扩散的每个时间步 $t$，我们使用引导模型计算 $x_t$ 的梯度，方向是增加 $x_t$ 拥有某些目标特征 $y_{\text{target }}$ 的概率。然后我们在通常的去噪更新之外，更新 $x_t$，使其朝着这个方向前进。更正式地，反向扩散过程（公式3）修改为如下形式：

$$\begin{array}{rl}{x}_{t-1}=& \frac{1}{\sqrt{1-{\beta }_t}}\left(x_t-\frac{{\beta }_t}{\sqrt{1-{\alpha }_t}}{ϵ}_{\theta }\left(x_t,t\right)\right)\\ & +{\sigma }_{t}z-s{\sigma }_t{\nabla }_{x_t}{\mathcal{L}}_{\text{guide }}\left(f_{\varphi }\left(x_t\right),y_{\text{target }}\right)\end{array}(4)$$

其中 ${\mathcal{L}}_{\text{guide }}$ 和 $s$ 分别表示引导损失和引导强度。这种公式允许外部模型引导扩散模型以执行各种感兴趣的任务。例如，在类别条件图像生成中，$f_{\varphi }$ 是一个输出 $P_{\varphi }\left(y_{\text{target }}\mid x_t\right)$ 的图像分类器，${\mathcal{L}}_{\text{guide }}$ 由 $-\log \left(p_{\varphi }\left(y_{\text{target }}\mid x_t\right)\right)$ 给出。

3.2. Observation

---

本节探讨了简单的扩散指导方案是如何失败的。具体来说，我们表明，当用于引导扩散时，现成的模型会由于低置信度预测而失败，而使用受到大量噪声破坏的数据训练的模型则会失败。然后，我们报告了我们的主要观察结果，即使用受到不同噪声水平破坏的输入训练的分类器表现出不同的行为。我们表明这直接影响扩散指导，即拥有专门针对不同噪声区域的专家指导模型对于成功指导至关重要。

实验设置

我们的观察性研究涉及一个扩散模型和在噪声损坏数据上微调的各种分类器。对于引导分类器，我们使用了 ResNet50 [15]，它在 ImageNet 上预训练，并在必要时进行了微调。我们使用了一个在 ImageNet $256\times 256$ 上训练的扩散模型，最大时间步为 $T=1000$，如文献 [8] 中所述。为了生成数据的噪声版本，我们执行了正向扩散过程，即给定输入 $x_0$，我们得到 $x_t$ （公式 2），对于 $t=1,\dots ,T$。我们使用 DDIM 采样器 [50]，设置为 25 步，并使用所考虑的分类器来引导扩散模型。

更多细节请参考附录 B。

单纯的外部模型指导是不够的。在这里，我们研究了单纯扩散指导的失败案例。首先，我们尝试使用现成的 ResNet50 分类器对 ImageNet 类标签进行扩散指导。如图 4 的第一行所示，该模型无法为扩散指导提供有意义的梯度。这是因为现成的模型对在整个反向过程中遇到的分布不均、噪声隐变量输出低置信度、高熵预测，如图 2 所示。

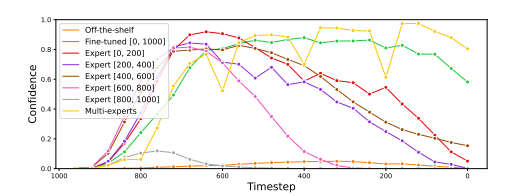
图 2. 逆向过程中的分类器置信度。现成的模型并没有增加置信度，表明它无法引导扩散到其置信区域。

我们还实验了一个在正向扩散过程中遇到的数据上微调的 ResNet50 分类器，即在所有 $t\in [1,\dots ,1000]$ 上的 $x_t$ （公式 1），其中 $x_0$ 对应于干净图像。正如在改进的 FID $(38.74\to 30.42)$ 和 IS $(33.95\to 43.05)$ 分数中观察到的那样，这比使用现成的模型效果更好（详见第5节）。然而，正如图2所示，对于较干净的图像（$t\approx 200$），分类器的置信度下降，导致如图4第二行中的失败情况。

图 4. $x_t$ 在 $t\in [920,720,520,320,120]$ 上的梯度图（左 5 张）以及生成的图像（最右一张），当逆向过程从相同的初始噪声被引导生成哈士奇时的结果。训练在较小噪声和较大噪声上的分类器分别倾向于修改更细的细节和更粗的结构。

根据学习到的噪声研究分类器行为

为了理解单一噪声感知模型的失败，我们研究了微调在特定噪声级别上的分类器的行为，即对于某些适当的 $a>0$ 和 $b<T$，$t\in [a,b]\subset [0,T]$ 上的 $x_t$。

具体来说，我们微调了五个 ResNet50 分类器 $f_{{\varphi }_i}$， i ∈ { 1 , … , 5 } i \in\{1, \ldots, 5\} i∈{1,…,5}，其中 $f_{{\varphi }_i}$ 在噪声输入 $x_t$ 上训练，$t\in \{(i-1)\cdot 200,\dots ,i\cdot 200\}$。我们首先通过 Grad-CAM [47] 观察到每个 $f_{{\varphi }_i}$ 的行为差异。例如，正如图3所示，$f_{{\varphi }_1}$ 和 $f_{{\varphi }_2}$ 在较干净的图像上训练，它们基于独特的犬类特征（如眼睛或毛皮花纹）预测 ‘哈士奇’。同时，$f_{{\varphi }_4}$ 和 $f_{{\varphi }_5}$ 在噪声图像上训练，它们根据整体形状进行预测（尽管人眼几乎不可察觉）。

图 3. 通过前向过程对每个专家在损坏图像上的 Grad-CAM 可视化。在较大和较小时间步长上训练的专家分别倾向于关注粗糙和精细特征。

这种行为差异在使用不同的 $f_{{\varphi }_i}$ 引导扩散时表现出来。例如，$f_{{\varphi }_5}$ 在噪声图像上训练，最初生成一个类似哈士奇的形状，但未能填充更细的细节。另一方面，$f_{{\varphi }_1}$ 在较干净的图像上训练，似乎专注于生成特定的细节（如毛发质感），但由于缺乏整体结构，未能生成类似哈士奇的图像。

这些分类器的行为与之前的观点一致；无条件扩散分别在较大和较小的噪声中关注整体结构和细节 [5]。考虑到这一点，我们假设分类器可以通过学习特定的噪声级别来引导扩散在该噪声级别进行生成。

3.3. Multi-Experts Strategy

---

4. Practical Plug-and-Play Diffusion

每当应用一个新的现成模型时，多专家策略必须利用多个网络并收集标记数据集。为了解决这种不切实际的问题，我们提出了一个即插即用的扩散指导框架：实用即插即用 (PPAP)，它采用多专家策略，具有以下两个组件，如图 5 所示：(1) 我们引入了一种基于参数共享的参数高效微调方案，以防止指导模型的大小过大；(2) 我们建议使用一种知识转移方案，将现成模型关于干净扩散生成的数据的知识转移到专家指导模型，从而无需标记数据集。

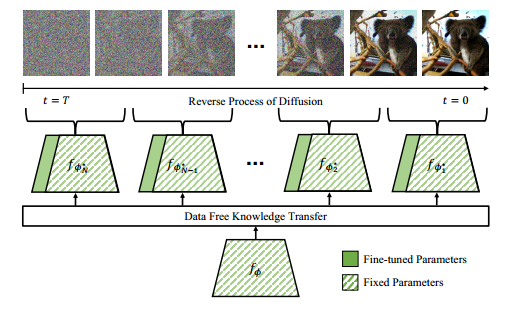
图 5. 我们的方法概述。我们使用参数高效的多专家，每个专家都专注于特定的噪声范围。我们将现成模型的知识转移到每个专家，从而绕过对标记数据的需求。在逆向过程中，我们只需要根据噪声区域相应地切换添加的训练参数。

4.1. Parameter Efficient Multi-Experts Strategy

---

提出的多专家策略的一个限制是，随着引导模型数量增加 $N$ 倍，需要微调的参数数量也增加 $N$ 倍。为了解决这个问题，我们采用了一种参数高效的策略，仅微调少量参数，同时重用大部分冻结的现成模型。具体而言，我们微调偏置项和批归一化（Batch Normalization），并对现成模型的某些权重矩阵应用 LoRA [20]。由于该方法不改变模型架构（如增加模型深度），因此不会引入额外的推理时间成本。我们将第 $n$ 个专家模型记为 $f_{{\varphi }_n^{\ast }}$，以区分现成模型 $f_{\varphi }$。

在扩散模型的反向过程中，我们只需根据噪声区域相应地切换已添加的训练参数，同时重用现成的主干模型。更多的架构细节见附录 C。

4.2. Data Free Knowledge Transfer

---

到目前为止，我们假设可以访问用于训练引导模型的数据集 { ( x 0 , y ) } \left\{\left(x_0, y\right)\right\} {(x0​,y)}。为了实现实用的即插即用生成，应该可以在不获取适合每个任务的标注数据集的情况下，使用现成模型进行引导。

我们在此提出使用扩散模型生成干净的数据集 { x ~ 0 } \left\{\tilde{x}_0\right\} {x~0​}，然后用它来训练专家引导模型。我们的基本假设是，通过模仿现成模型在干净图像上的预测，专家模型可以在一定程度上在噪声域中运行。具体而言，我们将现成模型 $f_{\varphi }$ 作为教师，并使用其在干净数据上的预测作为训练专家引导模型 $f_{{\varphi }_n}$ 时的标签。正式地，我们将知识迁移损失公式化为：

L K T = E t ∼ unif ⁡ { n − 1 N T , … , n N T } [ L ( sg ⁡ ( f ϕ ( x ~ 0 ) ) , f ϕ n ∗ ( x ~ t ) ) ] \mathcal{L}_{K T}=\mathbb{E}_{t \sim \operatorname{unif}\left\{\frac{n-1}{N} T, \ldots, \frac{n}{N} T\right\}}\left[\mathcal{L}\left(\operatorname{sg}\left(f_\phi\left(\tilde{x}_0\right)\right), f_{\phi_n^*}\left(\tilde{x}_t\right)\right)\right] LKT​=Et∼unif{Nn−1​T,…,Nn​T}​[L(sg(fϕ​(x~0​)),fϕn∗​​(x~t​))]

其中 $\mathrm{sg}(\cdot )$ 是停止梯度操作符，$\mathcal{L}$ 是任务特定的损失函数。通过这种形式化，我们可以轻松地将我们的方法适应各种感兴趣的任务，包括图像分类、单目深度估计和语义分割，只需使用不同的损失函数。由于篇幅限制，这里我们仅描述如何即插即用一个图像分类器。其他任务的详细信息可以在附录 D 中找到。

图像分类 图像分类器以图像为输入，并输出形式为 $f(x)\in {\mathbb{R}}^C$ 的 logit 向量，其中 $C$ 是图像类别的数量。我们将分类器的知识迁移损失 ${\mathcal{L}}_{clsf}$ 公式化为：

$${\mathcal{L}}_{clsf}=D_{KL}\left(\mathrm{sg}\left(s\left(f_{\varphi }\left({\tilde{x}}_0\right)/\tau \right)\right),\mathrm{s}\left(f_{{\varphi }_n^{\ast }}\left({\tilde{x}}_t\right)\right)\right)$$
其中，$s$ 是 softmax 操作符，$\tau$ 是温度超参数，$D_{KL}(\cdot )$ 是 Kullback-Leibler 散度。

总结

• 外部引导模型+LoRA
• 外部引导模型的独立性