在引出本章的内容之前先介绍一个概念

知识

知识的概念

知识（Knowledge）是人们在改造客观世界的实践中形成的对客观事物（包括自然的和人造的）及其规律的认识，包括对事物的现象、本质、状态、关系、联系和运动等的认识。

经过人的思维整理过的信息、数据、形象、意象、价值标准以及社会的其他符号产物，不仅包括科学技术知识----知识中最重要的部分，还包括人文社会科学的知识、商业活动、日常生活和工作中的经验和知识，人们获取、运用和创造知识的知识，以及面临问题做出判断和提出解决方法的知识。

知识是把有关的信息关联在一起，形成的关于客观世界某种规律性认识的动态信息结构。

知识=事实+规则+概念            
     事实就是指人类对客观世界、客观事物的状态、属性、特征的描述，以及对事物之间关系的描述。
     规则是指能表达在前提和结论之间的因果关系的一种形式；
     概念主要指事实的含义、规则、语义、说明等。

知识的分类

1、 按知识的作用范围分：
  （1）常识性知识：通用性知识，适用于所有领域；      
        如一年有四个季节。
  （2）领域性知识：面向某个具体领域的知识，是专业性知识，如疾病诊断的知识。

2 、按知识的作用及表示划分：
（1）事实性知识：用于描述领域内的有关概念、事实、事物的属性及状态；
    如：太阳从东方升起
（2）过程性知识：与领域相关的、用于指出如何处理与问题相关的信息以及求得问题的解；
    如：如果信道畅通，请发绿色信号
（3）控制性知识：又称为深层知识及元知识，是关于如何运用已有的知识进行问题求解的知识，也称为关于知识的知识。    
    如： 问题求解过程中的处理方法、搜索策略、控制结构

3 、按知识的确定性来分：
（1）确定性知识：指其逻辑值为真或假的知识，是精确性知识；
   如：他是男的
（2）不确定性知识：是不精确、不完全、模糊性知识的总称。
   如：今天阴天，可能要下雨

4 、按人类的思维及认识方法来分：
（1）逻辑性知识：是反映人类逻辑思维过程的知识，一般具有因果关系或难以精确描述的特点，是人类的经验性知识和直观感觉；
      如：人的为人处事的经验与风格
（2）形象性知识：通过事物的形象建立起来的知识。
     如:什么是牛？

5、 知识的获取方式来分：
（1）显性知识：指可通过文字、语言、图形、声音等形式编码记录和传播的知识；
   如：教材、音视频光盘。
（2）隐性知识：指人们长期实践中积累获得的知识，不易用显性知识表达的知识。
   如：每个人都有不同的审美观。

不管从什么角度去划分知识，要用机器对知识进行处理，都必须以适当的形式对知识进行表示，这就是知识表示技术。
在选择知识表示的方法时应考虑几个因素：
（1）能否充分表示相关领域的知识；
（2）是否有利于对知识的利用；
（3）是否便于知识的组织和管理；
（4）是否便于理解和实现。

一、产生式规则

1、产生式规则

 产生式(Production)一词, 首先是由美国数学家波斯特(E.Post)提出来的。波斯特根据替换规则提出了一种称为波斯特机的计算模型, 模型中的每一条规则当时被称为一个产生式。 后来, 这一术语几经修改扩充, 被用到许多领域。例如, 形式语言中的文法规则就称为产生式。产生式也称为产生式规则, 或简称规则。

产生式的一般形式为

前件〉→〈后件〉 

其中, 前件就是前提, 后件是结论或动作,前件和后件可以是由逻辑运算符AND、OR、NOT组成的表达式。  

 产生式规则的语义是: 如果前提满足,则可得结论或者执行相应的动作, 即后件由前件来触发。 所以, 前件是规则的执行条件, 后件是规则体。

 例如, 下面就是几个产生式规则：  
    (1) 如果银行存款利率下调, 那么股票价格上涨。  
    (2) 如果炉温超过上限, 则立即关闭风门。  
    (3) 如果键盘突然失灵, 且屏幕上出现怪字符, 则是病毒发作。  
    (4) 如果胶卷感光度为200, 光线条件为晴天, 目标距离不超过5米, 则快门速度取250, 光圈大小取f16。

       可以看出,产生式与逻辑蕴含式非常相似。是的, 逻辑蕴含式就是产生式, 但它只是一种产生式。除逻辑蕴含式外, 产生式还包括各种操作、规则、变换、算子、函数等等。 比如上例中的(2)是一个产生式, 但并不是一个逻辑蕴含式。 概括来讲, 产生式描述了事物之间的一种对应关系(包括因果关系和蕴含关系), 其外延十分广泛。例如, 图搜索中的状态转换规则和问题变换规则就都是产生式规则。另外还有程序设计语言的文法规则、逻辑中的逻辑蕴含式和等价式、数学中的微分和积分公式、化学中分子结构式的分解变换规则等等, 也都是产生式规则；甚至体育比赛中的规则、国家的法律条文、 单位的规章制度等等, 也都可以表示成产生式规则。

     在自然语言表达中，人们广泛使用的各种“原因→结果”，“条件→结论”，“前提→操作”，“事实→进展”，“情况→行为”等结构，都可归结为产生式的知识表达形式。
例如，
天下雨，地上湿；  “原因→结果”
如果把水加热到00以上，冰就会溶化为水；“条件→结论”
夜来风雨声，花落知多少；“事实→进展”
若能找到一根合适的杠杆，就能撬起那座大山；“前提→操作”
才饮长沙水，又食武昌鱼；“事实→进展”
刚才开机了，意味着发出了捕获目标图像的信号。“情况→行为”

【注意】：谓词逻辑中的蕴涵式与产生式的基本形式相似，事实上，蕴涵式只是产生式的一种特殊情况。理由如下：
      （1）蕴涵式只能表示精确知识，其值非“真”即“假”，而产生式不仅可以表示精确知识，而且还可以表示不精确知识。
例如，MYCIN中有如下产生式：

   IF    本微生物的染色斑是革兰氏阴性
                    本微生物的形状呈杆状
                    病人是中间宿主
    THEN   该微生物是绿脓杆菌，可信度为CF=0.6

CF表示知识的强度，谓词逻辑中的蕴涵式不可以这样做。   
       （2）用产生式表示知识的系统中，“事实”与产生式的“前提”中所规定的条件进行匹配时，可以是“精确匹配”，也可以是基于相似度的“不精确匹配”，只要相似度落入某个预先设定的范围内，即可认为匹配。但对谓词逻辑的蕴涵式而言，其匹配必须是精确的。

2、基于产生式规则的推理模式      

      由产生式的涵义可知,利用产生式规则可以实现有前提条件的指令性操作, 也可以实现逻辑推理。实现操作的方法是当测试到一条规则的前提条件满足时, 就执行其后部的动作。 这称为规则被触发或点燃。利用产生式规则实现逻辑推理的方法是当有事实能与某规则的前提匹配(即规则的前提成立)时, 就得到该规则后部的结论(即结论也成立)。
      实际上,这种基于产生式规则的逻辑推理模式, 就是逻辑上所说的假言推理(对常量规则而言)和三段论推理(对变量规则而言), 即：

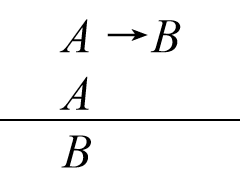
这里的大前提就是一个产生式规则, 小前提就是证据事实。
　　其实, 我们也可以把上面的有前提条件的操作和逻辑推理统称为推理。那么,上面的式子也就是基于产生式规则的一般推理模式。这就是说, 产生式系统中的推理是更广义的推理。

二、产生式系统

1、系统结构

产生式系统由三部分组成： 产生式规则库、 推理机和动态数据库, 其结构如图所示。

产生式系统的结构

产生式规则库亦称产生式规则集, 由领域规则组成, 在机器中以某种动态数据结构进行组织。一个产生式规则集中的规则, 按其逻辑关系, 一般可形成一个称为推理网络的结构图。

推理机亦称控制执行机构,它是一个程序模块,负责产生式规则的前提条件测试或匹配,规则的调度与选取,规则体的解释和执行。即推理机实施推理, 并对推理进行控制, 它也就是规则的解释程序。

动态数据库亦称全局数据库、综合数据库、工作存储器、上下文、黑板等等，它是一个动态数据结构，用来存放初始事实数据、中间结果和最后结果等。

2、运行过程

 产生式系统运行时, 除了需要规则库以外, 还需要有初始事实(或数据)和目标条件。目标条件是系统正常结束的条件, 也是系统的求解目标。产生式系统启动后, 推理机就开始推理, 按所给的目标进行问题求解。  
　　推理机的一次推理过程可如图所示。

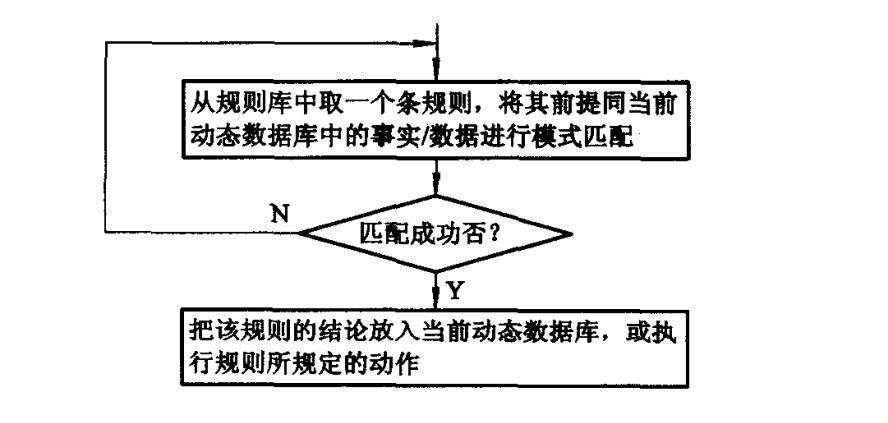
 推理机的一次推理过程

      一个实际的产生式系统, 其目标条件一般不会只经一步推理就可满足, 往往要经过多步推理才能满足或者证明问题无解。 所以, 产生式系统的运行过程,就是推理机不断运用规则库中的规则, 作用于动态数据库, 不断进行推理并不断检测目标条件是否满足的过程。当推理到某一步, 目标条件被满足, 则推理成功, 于是系统运行结束；或者再无规则可用, 但目标条件仍未满足, 则推理失败, 当然系统也运行结束。
       由上所述, 产生式系统的运行过程也就是从初始事实出发, 寻求到达目标条件的通路的过程。 所以, 产生式系统的运行过程也是一个搜索的过程。但一般把产生式系统的整个运行过程也称为推理。那么, 一个产生式系统启动后,从哪儿开始推理？ 下面我们就回答这个问题。

3、控制策略与常用算法

      产生式系统的推理可分为正向推理和反向推理两种基本方式。简单来讲, 正向推理就是从初始事实数据出发, 正向使用规则进行推理(即用规则前提与动态数据库中的事实匹配, 或用动态数据库中的数据测试规则的前提条件, 然后产生结论或执行动作),朝目标方向前进；反向推理就是从目标出发, 反向使用规则进行推理(即用规则结论与目标匹配, 又产生新的目标, 然后对新目标再作同样的处理),朝初始事实或数据方向前进。下面我们给出产生式系统正向推理和反向推理的常用算法：

a. 正向推理    

正向推理算法一： 

　步1 将初始事实/数据置入动态数据库。
  步2 用动态数据库中的事实/数据, 匹配/测试目标条件, 若目标条件满足, 则推理成功, 结束。  
  步3 用规则库中各规则的前提匹配动态数据库中的事实/数据, 将匹配成功的规则组成待用规则集。
  步4 若待用规则集为空, 则运行失败, 退出。  
  步5 将待用规则集中各规则的结论加入动态数据库, 或者执行其动作, 转步2。

可以看出, 随着推理的进行, 动态数据库的内容或者状态在不断变化。如果我们把动态数据库的每一个状态作为一个节点的话, 则上述推理过程也就是一个从初始状态(初始事实/数据)到目标状态(目标条件)的状态图搜索过程。 如果我们把动态数据库中每一个事实/数据作为一个节点的话, 则上述推理过程就是一个“反向”(即自底向上)与或树搜索过程。

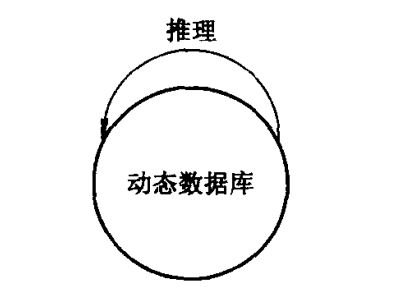
正向推理的动态数据库

例6.1　动物分类问题的产生式系统描述及其求解。
设由下列动物识别规则组成一个规则库, 推理机采用上述正向推理算法, 建立一个产生式系统。该产生式系统就是一个小型动物分类知识库系统。  

规则集：

    r1： 若某动物有奶, 则它是哺乳动物。  
    r2： 若某动物有毛发, 则它是哺乳动物。  
    r3： 若某动物有羽毛, 则它是鸟。  
    r4： 若某动物会飞且生蛋, 则它是鸟。 
    r5： 若某动物是哺乳动物且有爪且有犬齿且目盯前方, 则它是食肉动物。  
    r6： 若某动物是哺乳动物且吃肉, 则它是食肉动物。  
    r7： 若某动物是哺乳动物且有蹄, 则它是有蹄动物。  
    r8： 若某动物是有蹄动物且反刍食物, 则它是偶蹄动物。 
    r9： 若某动物是食肉动物且黄褐色且有黑色条纹, 则它是老虎。  
    r10： 若某动物是食肉动物且黄褐色且有黑色斑点, 则它是金钱豹。  
    r11： 若某动物是有蹄动物且长腿且长脖子且黄褐色且有暗斑点, 则它是长颈鹿。  
    r12： 若某动物是有蹄动物且白色且有黑色条纹, 则它是斑马。  
    r13： 若某动物是鸟且不会飞且长腿且长脖子且黑白色, 则它是驼鸟。  
    r14： 若某动物是鸟且不会飞且会游泳且黑白色, 则它是企鹅。  
    r15： 若某动物是鸟且善飞且不怕风浪, 则它是海燕。 

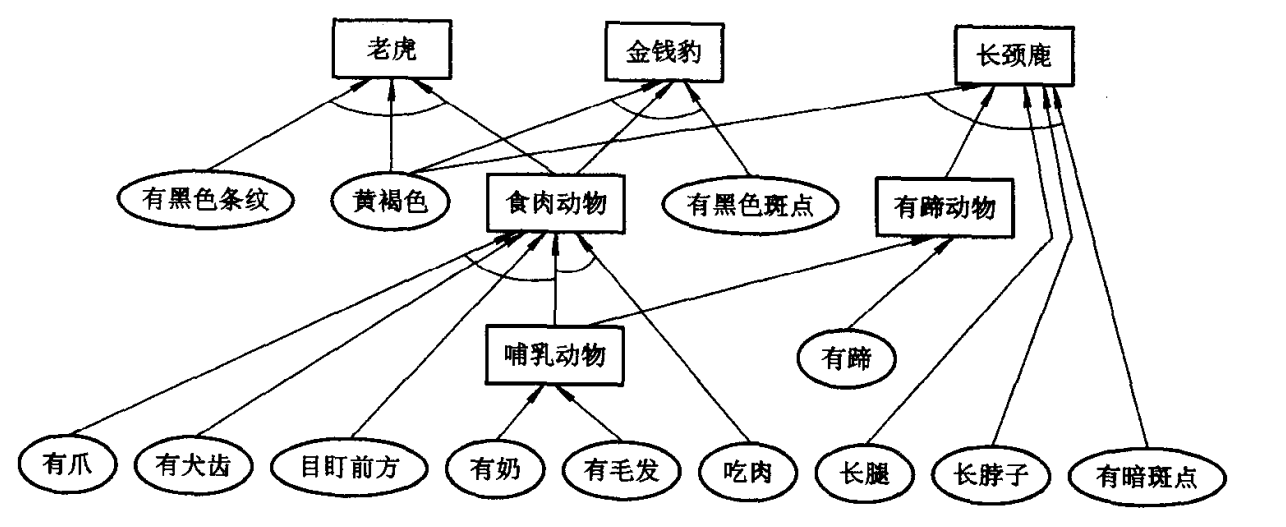
 规则集形成的部分推理网络

再给出初始事实：  

f1：某动物有毛发。
f2：吃肉。
f3：黄褐色。
f4：有黑色条纹。 

目标条件为： 该动物是什么？

易见, 该系统的运行结果为： 该动物是老虎。其推理树如图所示。

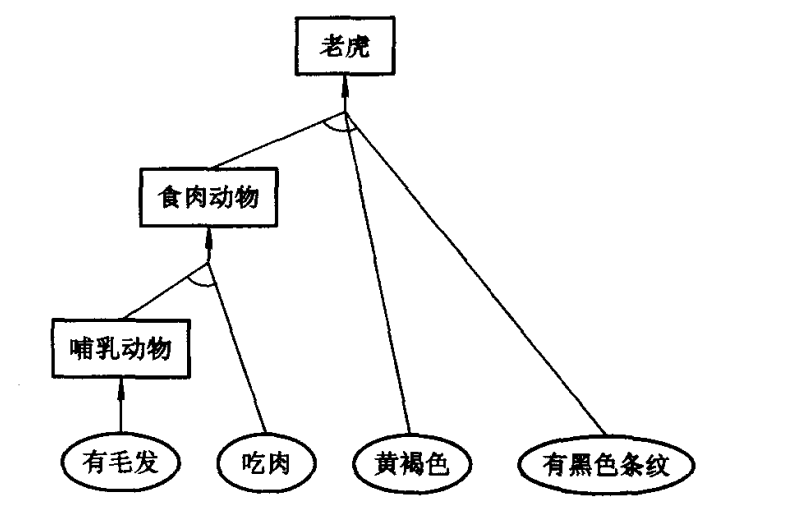
 关于“老虎”的正向推理树

b. 反向推理 　　

反向推理算法：

　步1 将初始事实/数据置入动态数据库, 将目标条件置入目标链。
  步2 若目标链为空, 则推理成功, 结束。  
  步3 取出目标链中第一个目标, 用动态数据库中的事实/数据同其匹配, 若匹配成功, 转步2。 
  步4 用规则集中的各规则的结论同该目标匹配, 若匹配成功,则将第一个匹配成功且未用过的规则的前提作为新的目标,  并取代原来的父目标而加入目标链, 转步3。 
　步5 若该目标是初始目标, 则推理失败, 退出。  
  步6 将该目标的父目标移回目标链, 取代该目标及其兄弟目标, 转步3。  

对于例6.1中的产生式系统, 改为反向推理算法, 则得到下图所示的推理树。

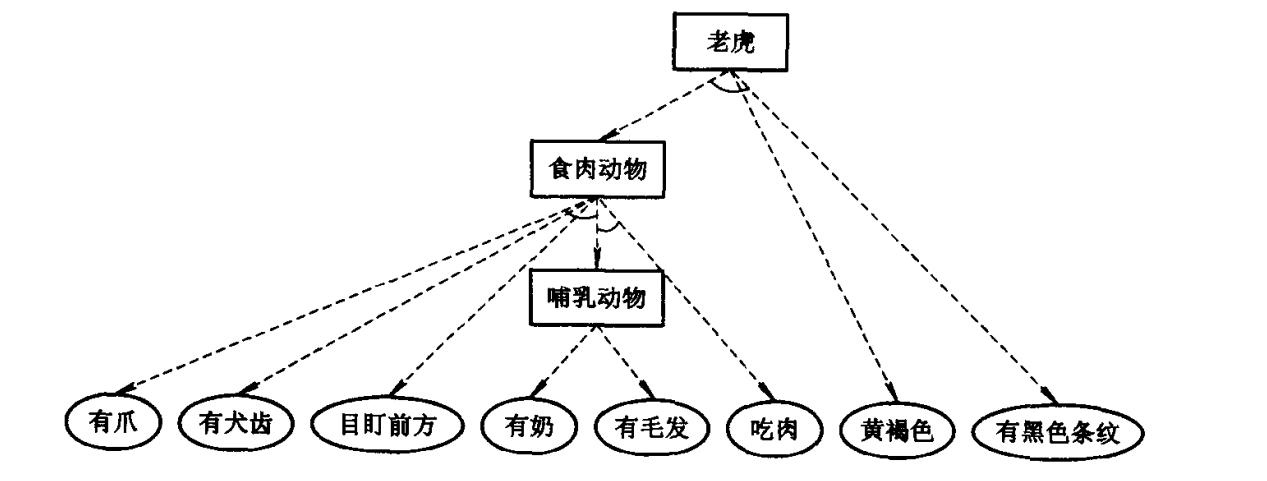
 关于“老虎”的反向推理树

可以看出, 与正向推理不同, 这次的推理树是从上而下扩展而成的, 而且推理过程中还发生过回溯。  
反向推理也称为后向推理、反向链、目标驱动的推理等。
从上面的两个算法可以看出,正向推理是自底向上的综合过程, 而反向推理则是自顶向下的分析过程。  
除了正向推理和反向推理外,产生式系统还可进行双向推理。双向推理就是同时从初始数据和目标条件出发进行推理, 如果在中间某处相遇, 则推理搜索成功。

c. 冲突消解策略

上述正向推理算法中, 对所有匹配成功的规则都同时触发启用。所以, 它实现的搜索是穷举式的树式盲目搜索。 下面我们给出一个正向推理的启发式线式搜索算法。  

正向推理算法二：

　步1 将初始事实/数据置入动态数据库。
  步2 用动态数据库中的事实/数据, 匹配/测试目标条件, 若目标条件满足, 则推理成功, 结束。
  步3 用规则库中各规则的前提匹配动态数据库中的事实/数据, 将匹配成功的规则组成待用规则集。
  步4 若待用规则集为空, 则运行失败, 退出。  
  步5 用某种策略,从待用规则集中选取一条规则, 将其结论加入动态数据库,或者执行其动作, 撤消待用规则集, 转步2。 

       可以看出,该算法与前面的算法仅在步5有所差别。但它已是不可回溯的线式搜索了。该算法的启发性表现在“用某种策略, 从待用规则集中选取一条规则”。这种选取策略, 也称为“冲突消解”策略。因为这时可用规则集中的规则都可触发执行, 但只取其中之一, 因而就产生了冲突或竞争。所以,冲突消解策略对正向推理有重要意义。  
       常用的冲突消解策略有：优先级法(优先级高者优先)、 可信度法(可信度高者优先)、代价法(代价低者优先)及自然顺序法等。当然, 要使用优先级法、可信度法、代价法等策略时, 须事先给规则设定相关的参数, 即优先级、可信度、代价等。
       可以看出,上述的两个推理算法的“启发”性就体现在冲突消解策略中。如果再采用优先级、可信度、代价等冲突消解策略, 则就是启发式搜索；但如果采用自然顺序法,则就是一种盲目碰撞搜索。  
       产生式系统的推理方式、搜索策略及冲突消解策略等, 一般统称为推理控制策略, 或简称控制策略。一个产生式系统的控制策略就体现在推理机的算法描述中。

4、程序实现

a. 产生式规则的程序语言实现    

上面我们对产生式的讨论, 只是用自然语言进行描述并仅在概念层次上进行阐述, 而并未涉及它的具体结构和程序语言实现问题。 现在讨论产生式规则的程序语言实现问题。
    首先, 讨论产生式规则的结构问题。一般来讲, 产生式规则的前提和结论部分可以是一个复杂的逻辑表达式, 但为了使表达简单规范, 且便于推理, 在实践中人们往往把规则的前提部分作成形如

　条件1 AND 条件2 AND … AND 条件n 

或  

   条件1 OR 条件2 OR … OR 条件m 

的形式(其中的条件可以带否定词)；

把规则结论部分作成形如

   断言1/动作1 AND 断言2/动作2 AND … AND 断言k/动作k

或  

 断言1/动作1 OR 断言2/动作2 OR … OR 断言k/动作k

的形式,或者进一步简化成

  断言/动作 

即仅有一项的形式。
 

由于含OR关系的规则也可以分解为几个不含OR关系的规则, 所以, 产生式规则也可仅取下面的一种形式：

条件1 AND 条件2 AND … AND 条件n→断言/动作 

即前件是若干与关系的条件, 后件仅有一个断言或动作。

       对规则作进一步细化。其条件、断言和动作都应该是陈述句。所以, 它们可以用n元谓词(或子句)形式表示, 或者用 n元组的形式表示, 如“对象-属性-值”三元组,“属性-值”二元组,或仅有“值”(符号、字符串或数值)的一元组等, 而且谓词和元组中的项可以是常量、变量或复合项。 当然, 对于条件还可以用通常的关系式表示。如果规则解释程序(即推理机)不能直接支持上述的谓词或元组表示形式, 那么,可用通常的记录、数组、结构、函数等数据结构来实现规则中的条件和断言, 用通常的赋值式、运算式、函数、过程等形式实现规则中的动作。
       至于规则的语言表示是否一定要有“IF-THEN”, 或者“AND”、 “OR”等连接符, 这倒不一定。 但原则是, 在程序执行时必须能体现出规则前提和结论的对应关系, 必须能体现出前提和结论中的逻辑关系。 例如, 我们完全可以用一个二元组  

(〈前件〉, 〈后件〉) 

表示一个产生式规则。
      上面我们给出了产生式规则在程序中的具体表示方法。 但必须指出的是, 产生式规则的程序语言形式与规则的解释程序(即推理机)密切相关。 就是说, 规则的解释程序与规则的语言形式必须是相符的、一致的。所以,一般不能单方面地孤立地谈论规则的语言表示形式, 而要与解释程序统一考虑。
    这样, 就有两种情况：一种是先确定规则的语言表示形式, 再根据规则形式设计规则解释程序(推理机)；另一种是对已有的解释程序(推理机), 设计规则表示形式(当然只能采用推理机所约定的规则形式)。

例如, 在PROLOG程序中要表示产生式规则, 至少有两种形式： 

  (1) 用PROLOG的规则表示产生式规则。
  (2) 用PROLOG的事实表示产生式规则。  

 　 对这两种表示, 对应的推理机是不一样的。若用方法(1), 则一般就不必编写显式的推理机程序, 因为对于这种形式的规则, PROLOG语言的翻译程序就是它的推理机。但若用方法(2), 则就必须用PROLOG语言编写显式的推理机程序。

例6.3　把上一节例6.1中给出的产生式规则用PROLOG的规则可表示如下：   

    animal_is(″老虎″):-
                       it_is(″食肉动物″),
                       fact(″黄褐色″),
                       fact(″有黑色条纹″).
    it_is(″食肉动物″):-it_is1(″哺乳动物″),
                       fact(″有爪″),
                       fact(″有犬齿″),
　　　　　　             fact(″目盯前方″).
    it_is(″食肉动物″):-it_is1(″哺乳动物″),
                       　fact(″吃肉″).
    it_is1(″哺乳动物″):-fact(″有奶″).
    it_is1(″哺乳动物″):-fact(″有毛发″). 

对于这种规则表示形式, 可以不用再编写推理机程序, 而可直接利用PROLOG自身的推理机,进行推理。

例如,当再给出如下的事实：  

    fact(″黄褐色″).
    fact(″有黑色条纹″).
    fact(″吃肉″).
    fact(″有奶″).  

和目标： 

 animal_is(Y). 

则程序运行后的结果就是:

 Y＝老虎 

但如果把上面的规则表示成如下的形式:

  rule(［″食肉动物″, ″黄褐色″, ″有黑色条纹″］, ″老虎″).
  rule(［″哺乳动物″, ″有爪″, ″有犬齿″, ″目盯前方″］, ″食肉动物″).
  rule(［″哺乳动物″, ″吃肉″］, ″食肉动物″).
  rule(［″有奶″］, ″哺乳动物″).
  rule(［″有毛发″］, ″哺乳动物″). 

则就需要用PROLOG语言编写一个推理机程序。 否则, 无法实施基于上述规则的推理。
还需说明的是, 并非凡是用PROLOG规则表示的产生式规则, 都可直接使用PROLOG的推理机。例如,                                                

 rule(X, Y):-Y=X+1. 

这是一个含变量的规则, 其中X为前提, Y是结论。也就是说, 在推理时是把rule(X,Y)作为规则使用的。显然, 对于这种形式的规则, 仍然需要重新编写推理机。

b. 规则库的程序实现

    规则库的程序实现分为内存和外存两个方面。 在内存中规则库可用链表实现, 在外存则就是以规则为基本单位的数据文件。但若用PROLOG程序, 对于用PROLOG的规则表示的产生式规则,规则库就是程序的一部分； 对于PROLOG事实表示的规则, 则规则库在内存就是动态数据库, 在外存就是数据库文件。  
    还需说明的是, 对于规则库实际上还需配一个管理程序, 即知识库管理系统, 专门负责规则及规则库的各项管理工作。 知识库管理系统的设计也与规则的表示形式密切相关。

c. 动态数据库的程序实现

    动态数据库由推理时所需的初始事实数据、推理的中间结果、 最后结果以及其他控制或辅助信息组成。这些事实数据的具体表示方法与上面所述的规则条件与结论的语言表示方法基本一样, 区别就是动态数据库中的事实数据中不能含有变量。 动态数据库在内存可由(若干)链表实现并组成。在PROLOG程序中实现动态数据库,则可不必编写链表程序, 而利用PROLOG提供的动态数据库直接实现。

d. 推理机的程序实现

    推理机的程序实现, 除了依据某一控制策略和算法编程外, 一般来说, 程序中还应具有模式匹配与变量的替换合一机制。 因为模式匹配是推理的第一步, 同时规则中一般都含有变量, 而变量的匹配必须有替换合一机制的支持。当然, 要实现合一, 就要用合一算法。 那么, 前面归结推理中的合一算法, 对产生式系统也是适用的(如果不是谓词公式合一, 则需稍作修改)。

      上面我们全面介绍了产生式系统的程序实现方法。最后值得一提的是, 由上所述可以看到： PROLOG的规则恰好能直接表示产生式规则, PROLOG的事实也恰好能表示产生式系统中的事实, PROLOG的动态数据库也刚好可用来实现产生式系统的动态数据库, 程序中的目标也就是产生式系统的运行目标, PROLOG的翻译程序本身就是一个推理机。这就是说, PROLOG语言本身恰好就是一个产生式系统框架或实现工具。 于是, 若用PROLOG实现产生式系统, 则程序员仅需把问题域中的产生式规则用PROLOG的规则表示, 把推理所需证据事实用PROLOG的数据库谓词表示, 再给出推理目标即可。

       最后需指出的是, 除了PROLOG语言外, LISP语言也是描述产生式规则,实现产生式系统的常用语言。另外, 还有几种产生式系统的专用语言,如OPS5、CLIPS等, 都是专门的产生式系统语言。用这些语言建立产生式系统,不必编写推理机程序, 只需按语言的规则语法建立规则库, 再给出初始事实和推理目标即可。

5、产生式系统与问题求解

分析前面给出的两个正向推理算法, 可以看出, 它们只能用于解决逻辑推理性问题。那么, 如何用正向推理来求解规划性问题呢？ 如果要用正向推理求解规划性问题, 则上述算法中至少还需增加以下功能：  
    (1) 记录动态数据库状态变化的历史, 这就需要增设一个CLOSED表。  
    (2) 若要回溯, 则还需保存与每个动态数据库状态对应的可用规则集。因为动态数据库状态与可用规则集实际是一一对应的。 当回溯到上一个动态数据库状态(节点)后,需从其可用规则集中重新选取一条规则。
 　(3) 要进行树式搜索,还需设置一个OPEN表, 以进行新生动态数据库的状态保存和当前动态数据库状态的切换。  
    (4) 还要考虑一条规则是否只允许执行一次。若是, 则要对已执行了的规则进行标记。但这样以来, 产生式系统的推理算法就与第 3 章的图搜索算法相差无几了。下面我们再将产生式系统与图搜索(含状态图搜索和与或图搜索)中的有关概念作一对比(如表 6.1所示)。

      可以看出,二者几乎是一回事。 要说差别的话, 图搜索主要着眼于搜索算法, 描述了问题求解的方法, 而产生式系统则主要着眼于知识, 并给出了实施这种方法的一种计算机程序系统的结构模式。这样, 问题求解、 图搜索和产生式系统三者的关系是： 问题求解是目的, 图搜索是方法, 产生式系统是形式。  
    既然基于产生式系统的推理就是图搜索,那么, 前面关于图搜索的各种策略, 对于产生式系统也仍然适用。

    还需指出的是, 在图搜索技术中, 与或图的搜索,一般都是从初始节点出发, 进行“自顶向下”地搜索。这种搜索用产生式系统实现, 一般用反向推理实现。 但同样的问题, 产生式系统也可用正向推理实现, 即进行“自下而上”地搜索。这就是说, 产生式系统能实施功能更强的搜索。这大概是产生式系统与前面介绍的图搜索的一个差别吧。  
    有些文献中, 把“自下而上”进行推理搜索, 且目标的到达与规则的触发次序无关的产生式系统称为可交换的产生式系统； 而把“自上而下”进行推理搜索,且搜索的是与或树的产生式系统称为可分解的产生式系统。
    由上述产生式系统与图搜索的关系可见, 产生式系统完全可以作为图搜索问题求解的一种通用模型。考虑到三种遗传操作和归结原理也都是产生式规则, 所以基于遗传算法的问题求解系统和基于归结原理的证明或求解系统实际上也都是产生式系统。 不过, 这是两种特殊的产生式系统, 或者说, 它们是产生式系统的变形(前者含有三条产生式规则, 后者仅含有一条产生式规则)。 这样, 产生式系统实际上就几乎成了人工智能问题求解系统的通用模型。

三、产生式系统的优缺点

1、产生式系统的优点

    （1）自然性：由于产生式系统采用了人类常用的表达因果关系的知识表示形式，既直观、自然，又便于进行推理。
    （2）模块性：产生式是规则库中的最基本的知识单元，形式相同，易于模块化管理。
    （3）有效性：能表示确定性知识、不确定性知识、启发性知识、过程性知识等。
    （4）清晰性：产生式有固定的格式，既便于规则设计，又易于对规则库中的知识进行一致性、完整性检测。

 2、产生式系统的缺点

   （1）效率不高
    产生式系统求解问题的过程是一个反复进行“匹配—冲突消解—执行”的过程。由于规则库一般都比较庞大，而匹配又是一件十分费时的工作，因此，其工作效率不高。此外，在求解复杂问题时容易引起组合爆炸。
   （2）不能表达具有结构性的知识
    产生式系统对具有结构关系的知识无能为力，它不能把具有结构关系的事物间的区别与联系表示出来，因此，人们经常将它与其它知识表示方法（如框架表示法、语义网络表示法）相结合。

 3、产生式系统的适用领域

   （1）由许多相对独立的知识元组成的领域知识，彼此之间关系不密切，不存在结构关系。如：化学反应方面的知识。
    （2）具有经验性及不确定性的知识，而且相关领域中对这些知识没有严格、统一的理论。如：医疗诊断、故障诊断等方面的知识。
    （3）领域问题的求解过程可被表示为一系列相对独立的操作，而且每个操作可被表示为一条或多条产生式规则。

腾讯云AI代码助手 —— 编程新体验，智能编码新纪元_腾讯云 ai 代码助手idea版-CSDN博客  https://blog.csdn.net/m0_75215937/article/details/140896158?spm=1001.2100.3001.7377&utm_medium=distribute.pc_feed_blog_category.none-task-blog-classify_tag-1-140896158-null-null.nonecase&depth_1-utm_source=distribute.pc_feed_blog_category.none-task-blog-classify_tag-1-140896158-null-null.nonecase