图的遍历是指从某点出发,按照某种搜索方式沿着边访问图中所有节点
图的遍历算法主要有两种:广度优先,深度优先
都需要辅助数组visited[]来记录节点是否被访问过
6.3.1广度优先搜索
like层次遍历,需要辅助队列
代码实现
#include<stdio.h>
#define maxnum 15
bool visited[maxnum];//定义辅助数组
void BFSTraverse(Graph G) {
for (int i = 0; i < G.vexnum; i++)
{
visited[i] = false;
}//初始化数组
initQueue(Q);//初始化队列
for (int i = 0; i < G.vexnum; i++)//从0号顶点开始遍历
{
if (!visited[i]) {
BFS(G,i);//广度优先遍历
}
}
}
void BFS(Graph G,int i){
visit(i);//访问
visited[i] = true;//改为t
EnQueue(Q,i);//入队
while (!isEmpty(Q)) {//判断队列是否为空
DeQueue(Q,i);//输出队列第一个元素
for ( p = FirstNeghbor(G,i); p >0; p=NextNeighbor(G,i,w))
{
if (!visited[p]) {
visit(p);
visited[p] = true;
EnQueue(Q, p);
}
}
}
}广度优先遍历过程

从顶点1出发:12563748
从顶点3出发:34678215
性能分析
邻接表和邻接矩阵空间复杂度![]()
邻接表时间复杂度![]()
邻接矩阵的时间复杂度
广度优先生成树
在广度遍历中可以得到一颗遍历树,为广度优先生成树
邻接矩阵唯一,生成树唯一
邻接表不唯一,生成树不唯一

6.3.2深度优先搜索
belike树的先序遍历
代码实现
#include<stdio.h>
#define maxnum 15
bool visited[maxnum];//定义辅助数组
void DFSTraverse(Graph G) {
for (int i = 0; i < G.vexnum; i++)
{
visited[i] = false;
}//初始化数组
for (int i = 0; i < G.vexnum; i++)//从0号顶点开始遍历
{
if (!visited[i]) {
DFS(G, i);//深度优先遍历
}
}
}
void DFS(Graph G, int i) {
visit(i);//访问
visited[i] = true;//改为t
for (p = FirstNeghbor(G, i); p > 0; p = NextNeighbor(G, i, w))
{
if (!visited[p]) {
DFS(G, p);
}
}深度优先遍历过程

从2出发:21563478
从3出发:34762158
性能分析

深度优先生成树和生成森林
非连通图可通过深度优先产生n棵生产树
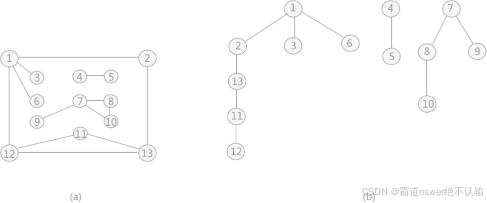
6.3.3图的遍历与图的连通性
to无向图:调用DFS/BFS的次数=连通分量数
to有向图:强连通分量只调用一次DFS/BFS;
若从起始节点到其他节点都有路径,则只需调用一次