一.TensorFlow创建神经层
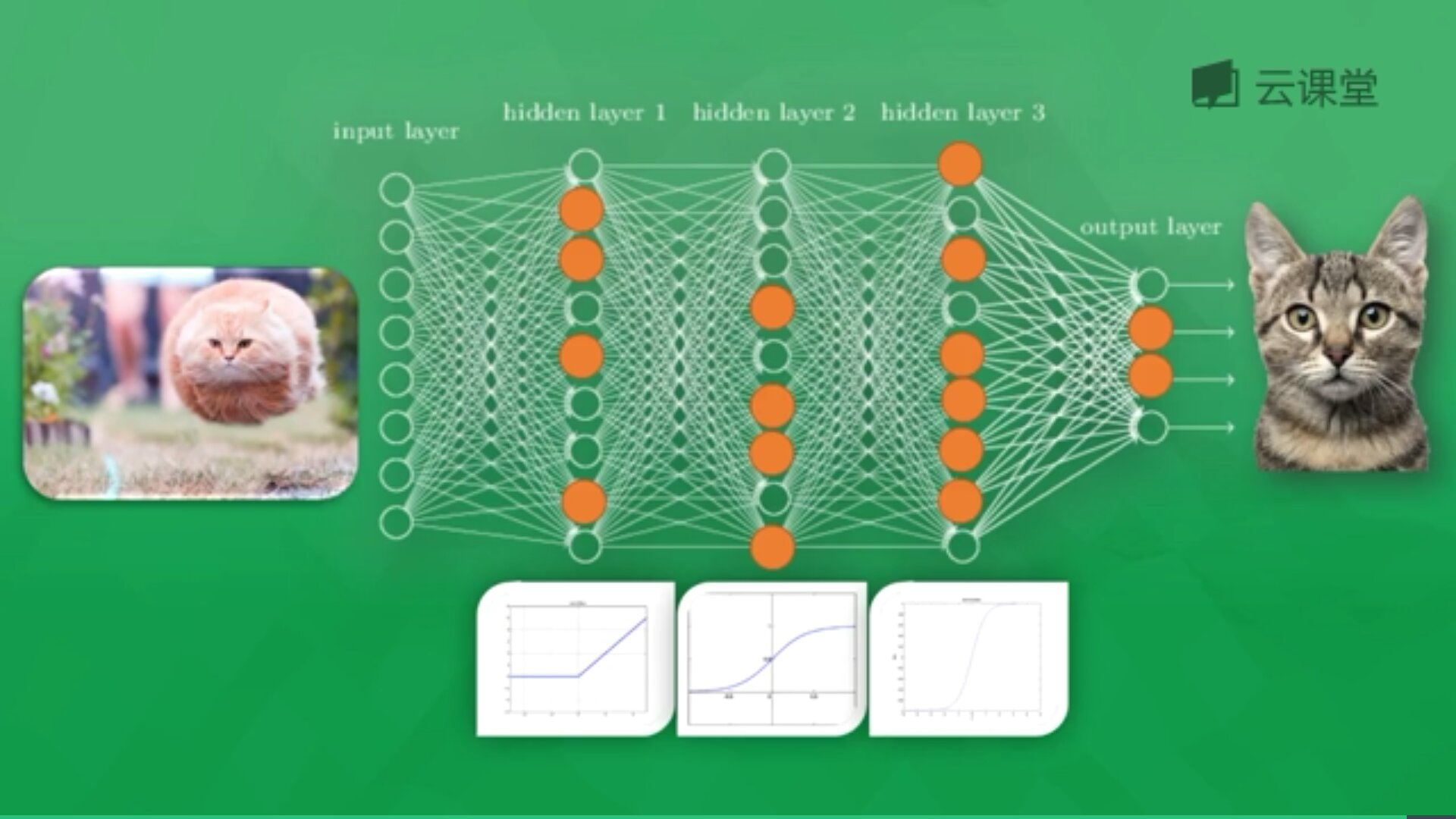
如图所示,通过该神经网络识别动物猫或狗,共包括输入层(Input Layer)、隐藏层3层(Hidden Layer)和输出层(Output Layer)。其中每个隐藏层神经元都有一个激励函数,被激励的神经元传递的信息最有价值,它也决定最后的输出结果,经过海量数据训练后,最终神经网络将可以用于识别猫或狗。
本文将通过TensorFlow不断训练学习,拟合一条曲线来预测散点的分布规律。首先,我们需要添加神经层,将层(Layer)定义成函数,用来添加神经层。神经层是相互连接的,从第一层输入层传入到隐藏层,最后传输至输出层。函数原型如下:
- add_layer(inputs, in_size, out_size, activation_function=None)
参数包括输入值,输入节点数,输出节点数和激励函数(默认为None)
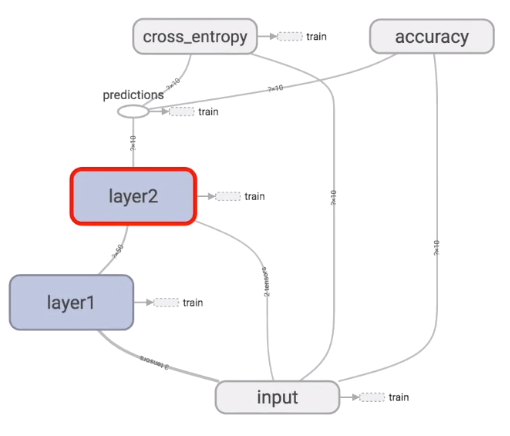
TensorFlow的结构如下,输入值input经过隐藏层layer1和layer2,然后有一个预测值predictions,cross_entropy是计算跟真实值的差距。
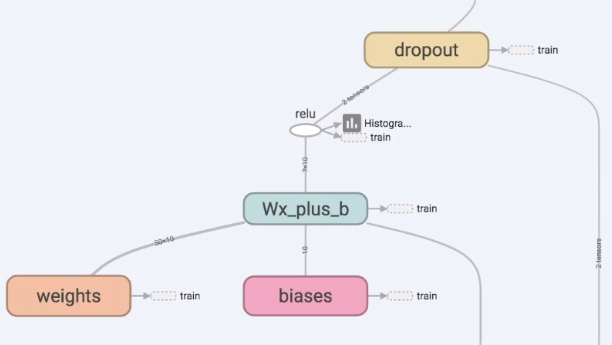
首先,我们需要制作的层是Layer1或Layer2,它们中间会有权重Weights和偏置biases,计算位于Wx_plus_b中,激励函数是relu。
下面开始撰写代码,如下所示:(详见注释)
# -*- coding: utf-8 -*-
"""
Created on Thu Dec 5 18:52:06 2019
@author: xiuzhang Eastmount CSDN
"""
import tensorflow as tf
#---------------------------------定义神经层-------------------------------
# 函数:输入变量 输入大小 输出大小 激励函数默认None
def add_layer(inputs, in_size, out_size, activation_function=None):
# 权重为随机变量矩阵
Weights = tf.Variable(tf.random_normal([in_size, out_size])) #行*列
# 定义偏置 初始值增加0.1 每次训练中有变化
biases = tf.Variable(tf.zeros([1, out_size]) + 0.1) #1行多列
# 定义计算矩阵乘法 预测值
Wx_plus_b = tf.matmul(inputs, Weights) + biases
# 激活操作
if activation_function is None:
outputs = Wx_plus_b
else:
outputs = activation_function(Wx_plus_b)
return outputs
二.回归神经网络实现
接下来开始实现了第一个神经网络代码,步骤如下:
1.制作虚拟数据
通过numpy.linspace生成300个随机点进行训练,形成y=x^2-0.5的虚拟数据。代码如下:
import tensorflow as tf
import numpy as np
#---------------------------------定义神经层---------------------------------
# 函数:输入变量 输入大小 输出大小 激励函数默认None
def add_layer(inputs, in_size, out_size, activation_function=None):
# 权重为随机变量矩阵
Weights = tf.Variable(tf.random_normal([in_size, out_size])) #行*列
# 定义偏置 初始值增加0.1 每次训练中有变化
biases = tf.Variable(tf.zeros([1, out_size]) + 0.1) #1行多列
# 定义计算矩阵乘法 预测值
Wx_plus_b = tf.matmul(inputs, Weights) + biases
# 激活操作
if activation_function is None:
outputs = Wx_plus_b
else:
outputs = activation_function(Wx_plus_b)
return outputs
#---------------------------------构造数据---------------------------------
# 输入
x_data = np.linspace(-1, 1, 300)[:,np.newaxis] #维度
# 噪声
noise = np.random.normal(0, 0.05, x_data.shape) #平均值0 方差0.05
# 输出
y_data = np.square(x_data) -0.5 + noise
# 设置传入的值xs和ys
xs = tf.placeholder(tf.float32, [None, 1]) #x_data传入给xs
ys = tf.placeholder(tf.float32,[None, 1]) #y_data传入给ys
#---------------------------------可视化分析---------------------------------
import matplotlib.pyplot as plt
# 定义图片框
fig = plt.figure()
ax = fig.add_subplot(1,1,1)
# 散点图
ax.scatter(x_data, y_data)
plt.show()
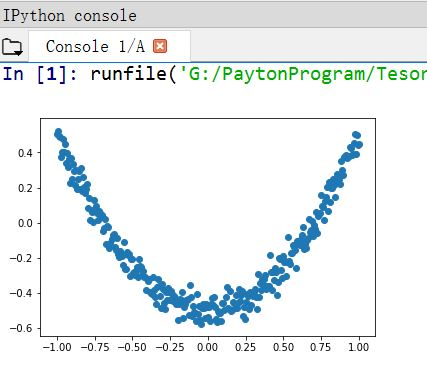
这里通过matplotlib简单绘制散点图,输出结果如下图所示,基本满足:y_data = np.square(x_data) -0.5 + noise。
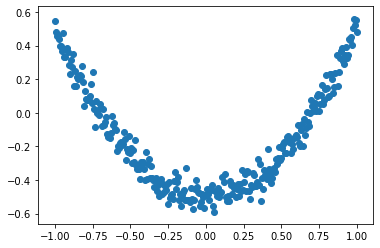
2.添加神经网络层
定义了隐藏层L1层和输出层prediction。
- L1 = add_layer(xs, 1, 10, activation_function=tf.nn.relu)
输入为xs,1维的data,神经元10个,relu非线性激励函数 - prediction = add_layer(L1, 10, 1, activation_function=None)
输入为L1输出值, in_size为L1的神经元10,假设L2输出为最终output
完整代码如下图所示:
# -*- coding: utf-8 -*-
"""
Created on Thu Dec 5 18:52:06 2019
@author: xiuzhang Eastmount CSDN
"""
import tensorflow as tf
import numpy as np
#---------------------------------定义神经层---------------------------------
# 函数:输入变量 输入大小 输出大小 激励函数默认None
def add_layer(inputs, in_size, out_size, activation_function=None):
# 权重为随机变量矩阵
Weights = tf.Variable(tf.random_normal([in_size, out_size])) #行*列
# 定义偏置 初始值增加0.1 每次训练中有变化
biases = tf.Variable(tf.zeros([1, out_size]) + 0.1) #1行多列
# 定义计算矩阵乘法 预测值
Wx_plus_b = tf.matmul(inputs, Weights) + biases
# 激活操作
if activation_function is None:
outputs = Wx_plus_b
else:
outputs = activation_function(Wx_plus_b)
return outputs
#---------------------------------构造数据---------------------------------
# 输入
x_data = np.linspace(-1, 1, 300)[:,np.newaxis] #维度
# 噪声
noise = np.random.normal(0, 0.05, x_data.shape) #平均值0 方差0.05
# 输出
y_data =np.square(x_data) -0.5 + noise
# 设置传入的值xs和ys
xs = tf.placeholder(tf.float32, [None, 1]) #x_data传入给xs
ys = tf.placeholder(tf.float32,[None, 1]) #y_data传入给ys
#---------------------------------可视化分析---------------------------------
import matplotlib.pyplot as plt
# 定义图片框
fig = plt.figure()
ax = fig.add_subplot(1,1,1)
# 散点图
ax.scatter(x_data, y_data)
# 连续显示
plt.ion()
plt.show()
#---------------------------------定义神经网络---------------------------------
# 一个输入层:x_data只有一个属性故只有一个神经元
# 一个输出层:y_data只有一个属性故只有一个神经元
# 一个隐藏层:10个神经元
# 隐藏层
L1 = add_layer(xs, 1, 10, activation_function=tf.nn.relu)
# 输出层
prediction = add_layer(L1, 10, 1, activation_function=None)
3.计算误差与神经网络学习
定义loss变量计算误差,即预测值与真实值的差别;再定义梯度下降变量(GradientDescentOptimizer),通过梯度下降让预测值更接近真实值。最后在Session中初始化及计算误差,每隔50步输出一次运算结果。
# -*- coding: utf-8 -*-
"""
Created on Thu Dec 5 18:52:06 2019
@author: xiuzhang Eastmount CSDN
"""
import tensorflow as tf
import numpy as np
#---------------------------------定义神经层---------------------------------
# 函数:输入变量 输入大小 输出大小 激励函数默认None
def add_layer(inputs, in_size, out_size, activation_function=None):
# 权重为随机变量矩阵
Weights = tf.Variable(tf.random_normal([in_size, out_size])) #行*列
# 定义偏置 初始值增加0.1 每次训练中有变化
biases = tf.Variable(tf.zeros([1, out_size]) + 0.1) #1行多列
# 定义计算矩阵乘法 预测值
Wx_plus_b = tf.matmul(inputs, Weights) + biases
# 激活操作
if activation_function is None:
outputs = Wx_plus_b
else:
outputs = activation_function(Wx_plus_b)
return outputs
#---------------------------------构造数据---------------------------------
# 输入
x_data = np.linspace(-1, 1, 300)[:,np.newaxis] #维度
# 噪声
noise = np.random.normal(0, 0.05, x_data.shape) #平均值0 方差0.05
# 输出
y_data =np.square(x_data) -0.5 + noise
# 设置传入的值xs和ys
xs = tf.placeholder(tf.float32, [None, 1]) #x_data传入给xs
ys = tf.placeholder(tf.float32,[None, 1]) #y_data传入给ys
#---------------------------------可视化分析---------------------------------
import matplotlib.pyplot as plt
# 定义图片框
fig = plt.figure()
ax = fig.add_subplot(1,1,1)
# 散点图
ax.scatter(x_data, y_data)
# 连续显示
plt.ion()
plt.show()
#---------------------------------定义神经网络---------------------------------
# 一个输入层:x_data只有一个属性故只有一个神经元
# 一个输出层:y_data只有一个属性故只有一个神经元
# 一个隐藏层:10个神经元
# 隐藏层
L1 = add_layer(xs, 1, 10, activation_function=tf.nn.relu)
# 输出层
prediction = add_layer(L1, 10, 1, activation_function=None)
#------------------------------定义loss和初始化-------------------------------
# 预测值与真实值误差 平均值->求和->平方(真实值-预测值)
loss = tf.reduce_mean(tf.reduce_sum(tf.square(ys - prediction),
reduction_indices=[1]))
# 训练学习 学习效率通常小于1 这里设置为0.1可以进行对比
train_step = tf.train.GradientDescentOptimizer(0.1).minimize(loss) #减小误差
# 初始化
init = tf.initialize_all_variables()
# 运行
sess = tf.Session()
sess.run(init)
#---------------------------------神经网络学习---------------------------------
# 学习1000次
n = 1
for i in range(1000):
# 训练
sess.run(train_step, feed_dict={xs:x_data, ys:y_data}) #假设用全部数据x_data进行运算
# 输出结果 只要通过place_holder运行就要传入参数
if i % 50==0:
print(sess.run(loss, feed_dict={xs:x_data, ys:y_data}))
输出结果如下图所示,每隔50步输出结果,第一次的误差是0.45145842,第二次的误差是0.012015346, 其误差在不断减少,说明神经网络在提升预测的准确性或学到东西了。
0.45145842
0.012015346
0.008982641
0.008721641
0.0085632615
0.008296631
0.0078961495
0.0074299597
0.0069189137
0.0063963127
0.0058622854
0.00548969
0.0051686876
0.0048802416
0.0046461136
0.0044451333
0.0042808857
0.004134449
0.0040101893
0.0039141406
写道这里,整个神经网络的定义和运行过程讲述完毕,包括定义神经层、误差设置、初始化及运行等,接下来开始可视化分析。
三.回归神经网络可视化分析
为了更直观了解神经网络是如何优化结果的,我们通过matplotlib进行可视化分析。从最早不合理的图形到后面基本拟合,loss误差在不断减小,说明神经网络的真实值和预测值在不断更新接近,神经网络正常运行。
第一次运行结果: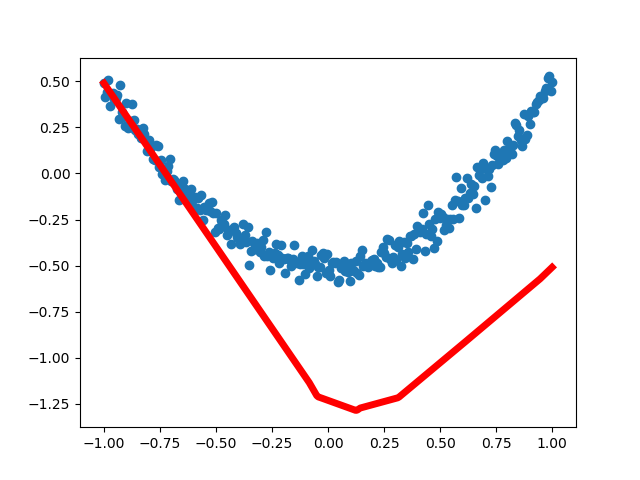
第四次运行结果: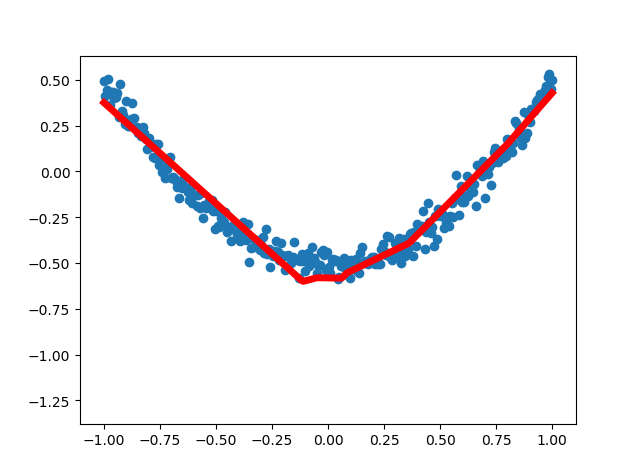
第二十次运行结果: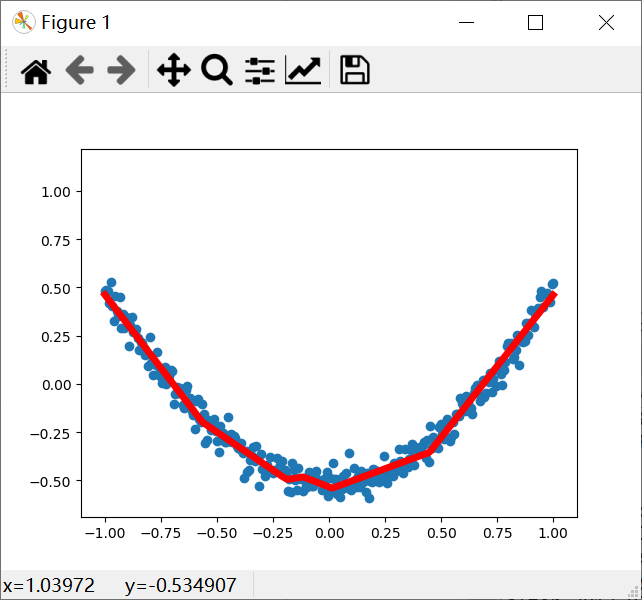
完整代码及注释如下所示:
# -*- coding: utf-8 -*-
"""
Created on Thu Dec 5 18:52:06 2019
@author: xiuzhang Eastmount CSDN
"""
import tensorflow as tf
import numpy as np
#---------------------------------定义神经层---------------------------------
# 函数:输入变量 输入大小 输出大小 激励函数默认None
def add_layer(inputs, in_size, out_size, activation_function=None):
# 权重为随机变量矩阵
Weights = tf.Variable(tf.random_normal([in_size, out_size])) #行*列
# 定义偏置 初始值增加0.1 每次训练中有变化
biases = tf.Variable(tf.zeros([1, out_size]) + 0.1) #1行多列
# 定义计算矩阵乘法 预测值
Wx_plus_b = tf.matmul(inputs, Weights) + biases
# 激活操作
if activation_function is None:
outputs = Wx_plus_b
else:
outputs = activation_function(Wx_plus_b)
return outputs
#---------------------------------构造数据---------------------------------
# 输入
x_data = np.linspace(-1, 1, 300)[:,np.newaxis] #维度
# 噪声
noise = np.random.normal(0, 0.05, x_data.shape) #平均值0 方差0.05
# 输出
y_data =np.square(x_data) -0.5 + noise
# 设置传入的值xs和ys
xs = tf.placeholder(tf.float32, [None, 1]) #x_data传入给xs
ys = tf.placeholder(tf.float32,[None, 1]) #y_data传入给ys
#---------------------------------可视化分析---------------------------------
import matplotlib.pyplot as plt
# 定义图片框
fig = plt.figure()
ax = fig.add_subplot(1,1,1)
# 散点图
ax.scatter(x_data, y_data)
# 连续显示
plt.ion()
plt.show()
#---------------------------------定义神经网络---------------------------------
# 隐藏层
L1 = add_layer(xs, 1, 10, activation_function=tf.nn.relu)
# 输出层
prediction = add_layer(L1, 10, 1, activation_function=None)
#------------------------------定义loss和初始化-------------------------------
# 预测值与真实值误差 平均值->求和->平方(真实值-预测值)
loss = tf.reduce_mean(tf.reduce_sum(tf.square(ys - prediction),
reduction_indices=[1]))
# 训练学习 学习效率通常小于1 这里设置为0.1可以进行对比
train_step = tf.train.GradientDescentOptimizer(0.1).minimize(loss) #减小误差
# 初始化
init = tf.initialize_all_variables()
# 运行
sess = tf.Session()
sess.run(init)
#---------------------------------神经网络学习---------------------------------
# 学习1000次
n = 1
for i in range(1000):
# 训练
sess.run(train_step, feed_dict={xs:x_data, ys:y_data}) #假设用全部数据x_data进行运算
# 输出结果 只要通过place_holder运行就要传入参数
if i % 50==0:
#print(sess.run(loss, feed_dict={xs:x_data, ys:y_data}))
try:
# 忽略第一次错误 后续移除lines的第一个线段
ax.lines.remove(lines[0])
except Exception:
pass
# 预测
prediction_value = sess.run(prediction, feed_dict={xs:x_data})
# 设置线宽度为5 红色
lines = ax.plot(x_data, prediction_value, 'r-', lw=5)
# 暂停
plt.pause(0.1)
# 保存图片
name = "test" + str(n) + ".png"
plt.savefig(name)
n = n + 1
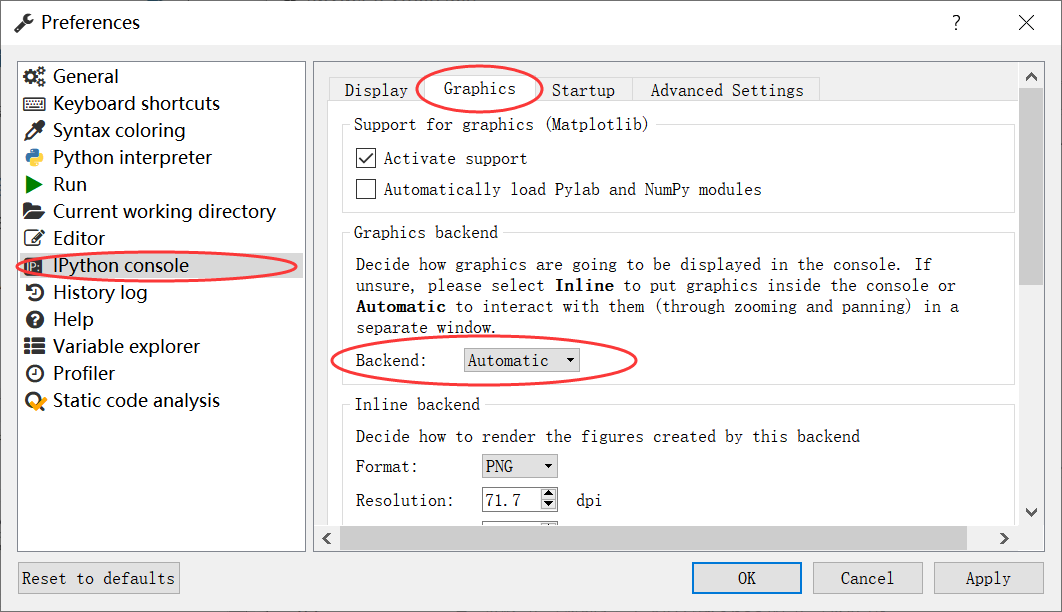
注意:在Spyder软件运行代码,一般显示figure的是在IPython console中,如下图所示,图比较小且不能进行操作,同时在IPython console中不能进行动态的figure显示。这时候需要设置单独弹出的窗口才能解决。
在Spyder软件设置单独弹出的窗口的步骤为:Tools–>Preferences–>IPython console–>Graphics–>Graphics backend–> Backend–>设置成Automatic,如下图所示。如果是设置成Inline则figure是在IPython console中显示。最后需要再对Spyder软件进行重新启动,没有重启则不能实现设置效果。这样就可以显示出单独的窗口,并可以实现动态的figure显示,如图所示的曲线动态拟合效果。
四.Optimizer优化器
class tf.train.Optimizer是优化器(optimizers)类的基类。这个类定义了在训练模型的时候添加一个操作的API。你基本上不会直接使用这个类,但是你会用到他的子类比如GradientDescentOptimizer、AdagradOptimizer、MomentumOptimizer等等。
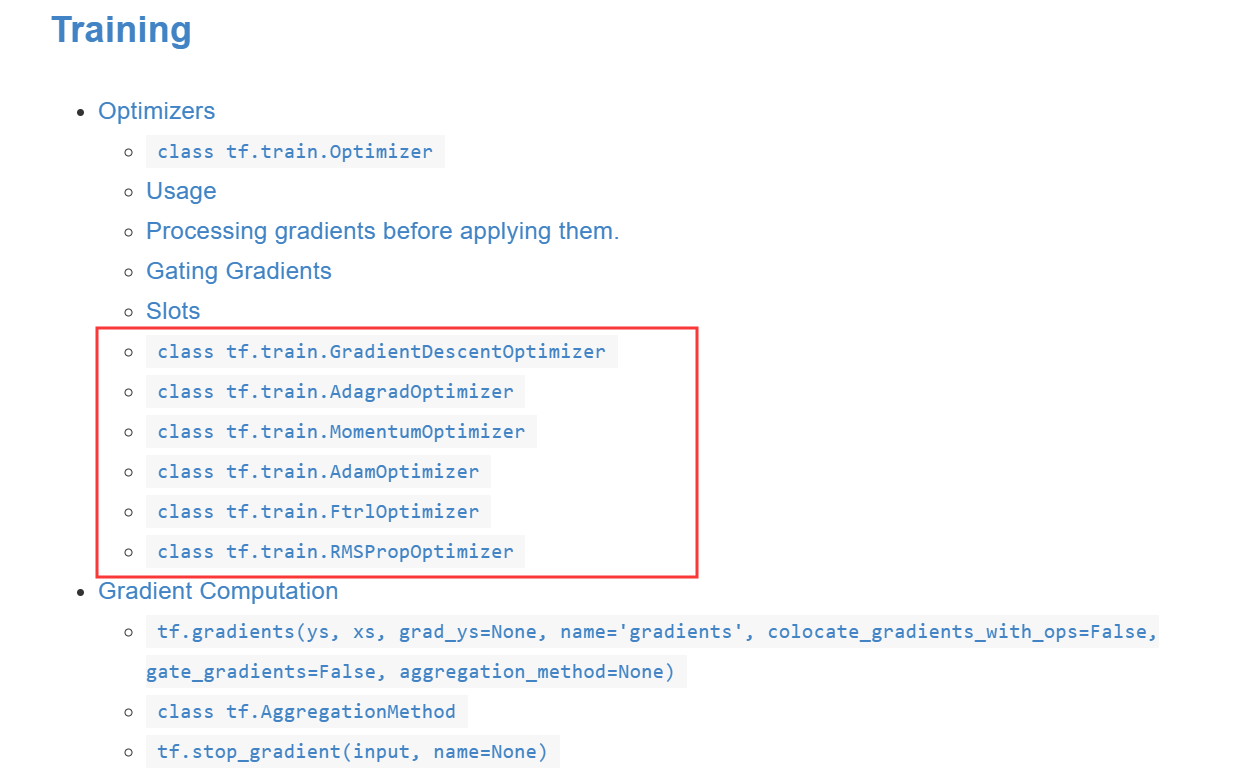
优化器有很多不同的种类,最基本的一种是GradientsDescentOptimizer,它也是机器学习中最重要或最基础的线性优化。官方给出的常见优化器如下图所示:
官方网址:
https://tensorflow.google.cn/versions/r1.15/api_docs/python/tf/train/Optimizer
它介绍七种常见的优化器包括:
- class tf.train.GradientDescentOptimizer
- class tf.train.AdagradOptimizer
- class tf.train.AdadeltaOptimizer
- class tf.train.MomentumOptimizer
- class tf.train.AdamOptimizer
- class tf.train.FtrlOptimizer
- class tf.train.RMSPropOptimizer
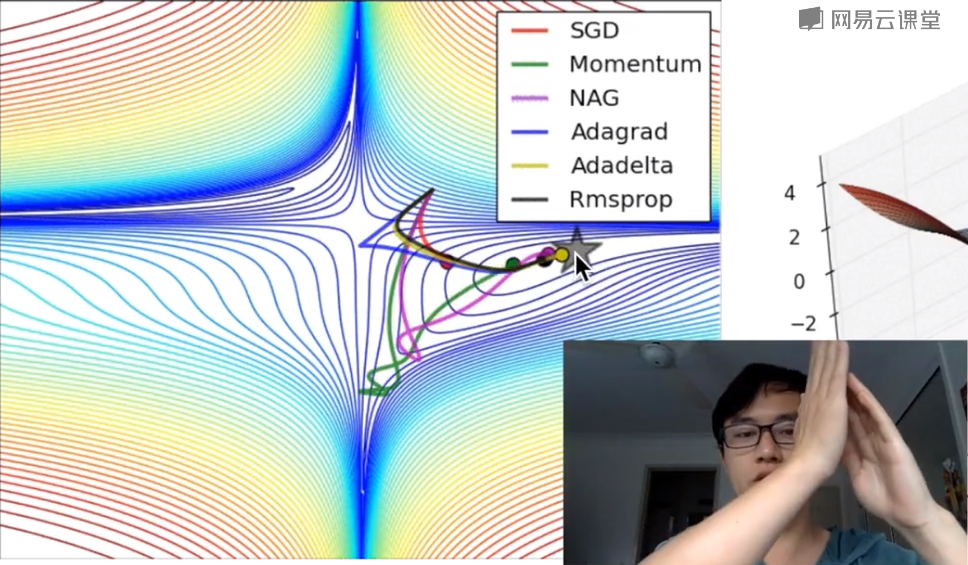
下面结合“莫烦”老师的课程,给读者们分享优化器的用法。
- GradientDescentOptimizer(梯度下降)取决于传进数据的size,比如只传进去全部数据的十分之一,GradientDescentOptimizer就变成了STD,它只考虑一部分的数据,一部分一部分的学习,其优势是能更快地学习到去往全局最小量(Global minimum)的路径。
- MomentumOptimizer 是基于学习效率的改变,它不仅仅考虑这一步的学习效率,还加载了上一步的学习效率趋势,然后上一步加这一步的learning_rate,它会比GradientDescentOptimizer更快到达全局最小量。
- RMSPropOptimizer Google用它来优化阿尔法狗的学习效率。
下图通过可视化对各种优化器进行了对比分析,机器学习从目标学习到最优的过程,有不同的学习路径,由于Momentum考虑了上一步的学习(learning_rate),走的路径会很长;GradientDescent的学习时间会非常慢。如果您是初学者,建议使用GradientDescentOptimizer即可,如果您有一定的基础,可以考虑下MomentumOptimizer、AdamOptimizer两个常用的优化器,高阶的话,可以尝试学习RMSPropOptimizer优化器。总之,您最好结合具体的研究问题,选择适当的优化器。