摘要:
1,差分数组的介绍
2,二维差分数组的介绍
1,差分数组的介绍
差分数组主要是操作区间的,关于区间操作的数据结构比较多,除了前面讲的《稀疏表》,还有树状数组,线段树,伸展树Splay等。尤其是后面两个在信奥赛和蓝桥杯的比赛中用到的还是比较多的 ,之后我们也都会一一介绍、这里先看一下差分数组。
假设有这样一个问题,给你一个数组nums,先对区间[a,b]中每个元素加 3 ,在对区间[c,d]每个元素减 5 …… ,这样非常频繁的区间修改,常规的做法可以一个个计算。
Java 代码:
// 给闭区间[a,b]中的每个元素都增加 k 。
public void increment(int[] nums, int a, int b, int k) {
for (int i = a; i <= b; i++) {
nums[i] += k;
}
}C++ 代码:
// 给闭区间[a,b]中的每个元素都增加 k 。
void increment(vector<int> &nums, int a, int b, int k) {
for (int i = a; i <= b; i++) {
nums[i] += k;
}
}频繁对数组的一段区间进行加减,如果一个个去操作,很明显效率很差,这个时候我们可以使用差分数组,差分数组就是原始数组相邻元素之间的差所构成的数组。定义差分数组d[n],则 d[i] = nums[i] − nums[i−1] ,其中 d[0] = nums[0] 。
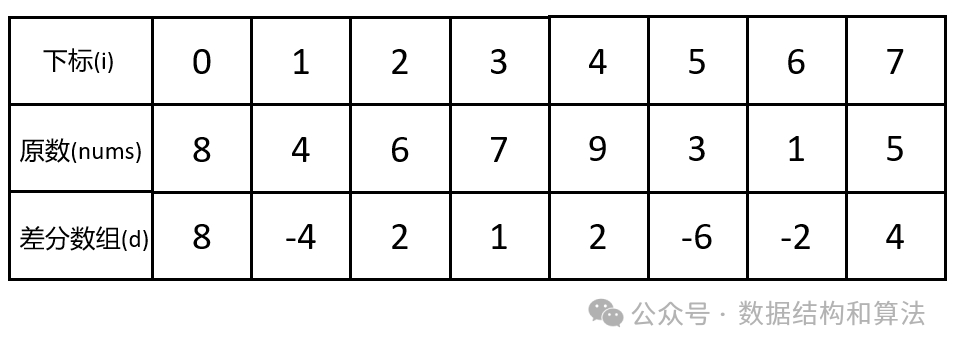
可以看到原数组的元素就是差分数组的前缀和,如果要计算nums[i],只需要把差分数组 d 的前 i 个元素相加即可。
nums[0] = d[0]
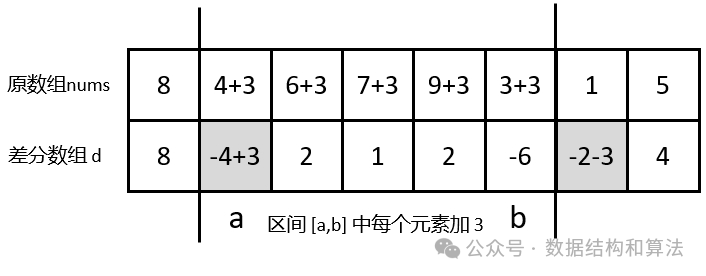
num[3] = d[0] + d[1] + d[2] + d[3]有了差分数组,如果对区间 [a,b] 中的每个元素加 3 ,不需要在一个个操作,只需要在两端修改。如下图所示,可以看到原数组需要修改区间内的所有值,而差分数组只需要修改两个值即可,一个是给d[a]加上 3 ,一个是给d[b+1]减去 3 。
d[a] += 3;
d[b+1] -= 3;// 注意不能越界