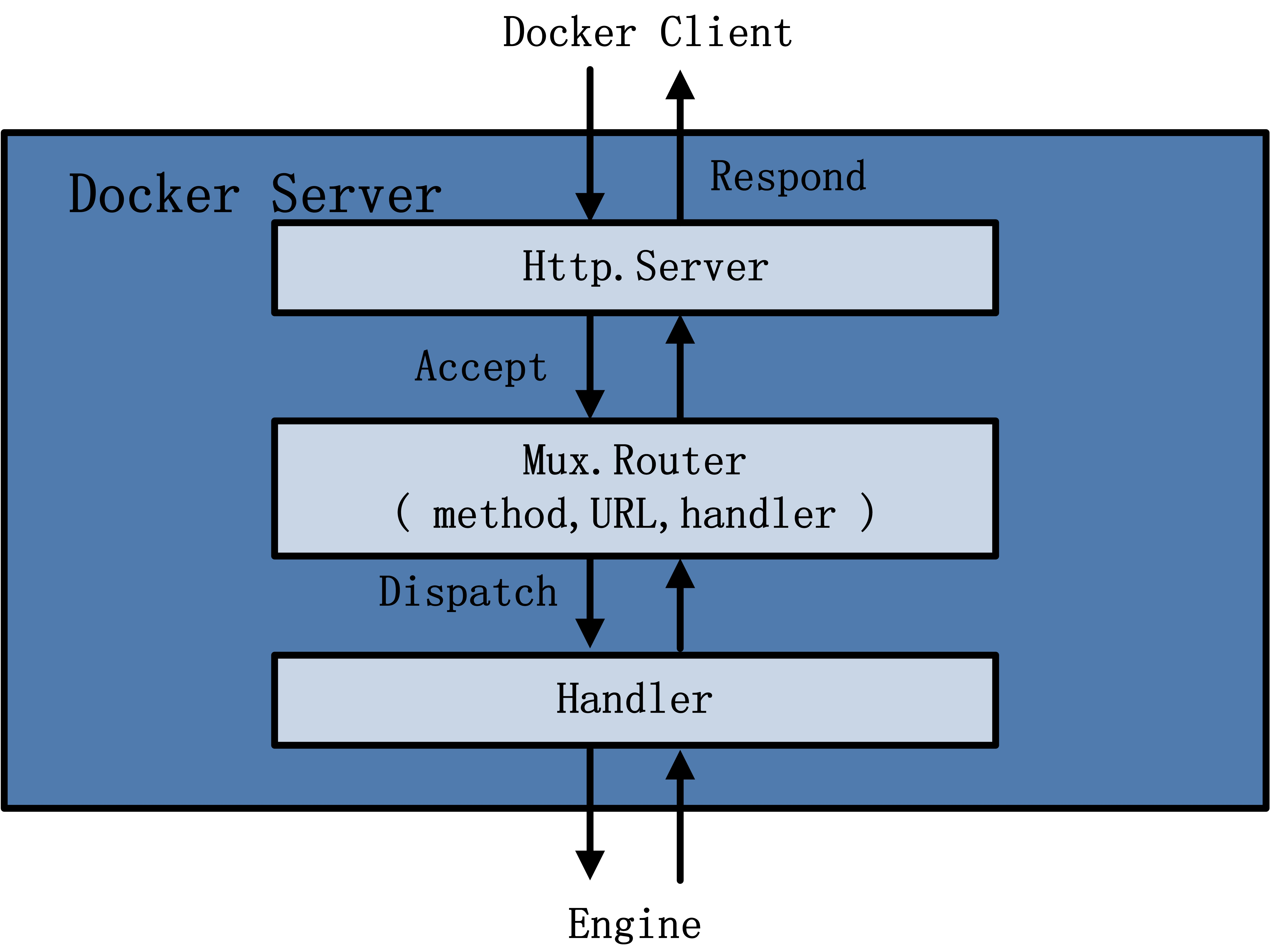
SSRFB DTSQT2 DLARFB DGEQT2
1, 对角子矩阵分解

DGEQT2
这个例程被开发出来,用于针对对角Tile子矩阵: ,执行不分块的QR分解。
这个运算产生:
一个上三角矩阵
一个酉下三角矩阵,这个矩阵包含 b 个 Householder 反光面、
一个上三角矩阵 ,在WY技术中,这个矩阵被定义用来累计Householder变换。
和
能够写进
所占据的内存空间,所以并不需要为他们分配额外的空间。
为了存储 ,则需要一个临时的工作空间。
因此, 执行的如下动作:
2, 将对角变换实施到同行子矩阵

DLARFB
通过上一个例程 DGEQT2 得到了一个变换 .
那么,这是LAPACK中的例程 DLARFB,将被用来将变换 实施到 Tile 子矩阵
上面。
因此, 执行如下动作:

DTSQT2
这个例程开发用来执行一个非分块矩阵的QR分解,
这个被分解的矩阵由那个上三角块矩阵 \mathbf{R_{kk}和方形矩阵 \mathbf{A_{ik}} 配对构成.
这个例程将会返回一个上三角矩阵\mathbf{~R_{kk}} ,这将用来重写 \mathbf{R_{kk}},还返回
b 个Householder 反射向量,b 是block tile 子矩阵的阶数。
注意,因为 \mathbf{R_{kk}} 是上三角矩阵,所以这导致 Householder 反射向量,
可以被表示为一个 单位子块矩阵 I,在子块方阵 \mathbf{V_{ik}} 的上边。
。。。。

DSSRFB
。。。。