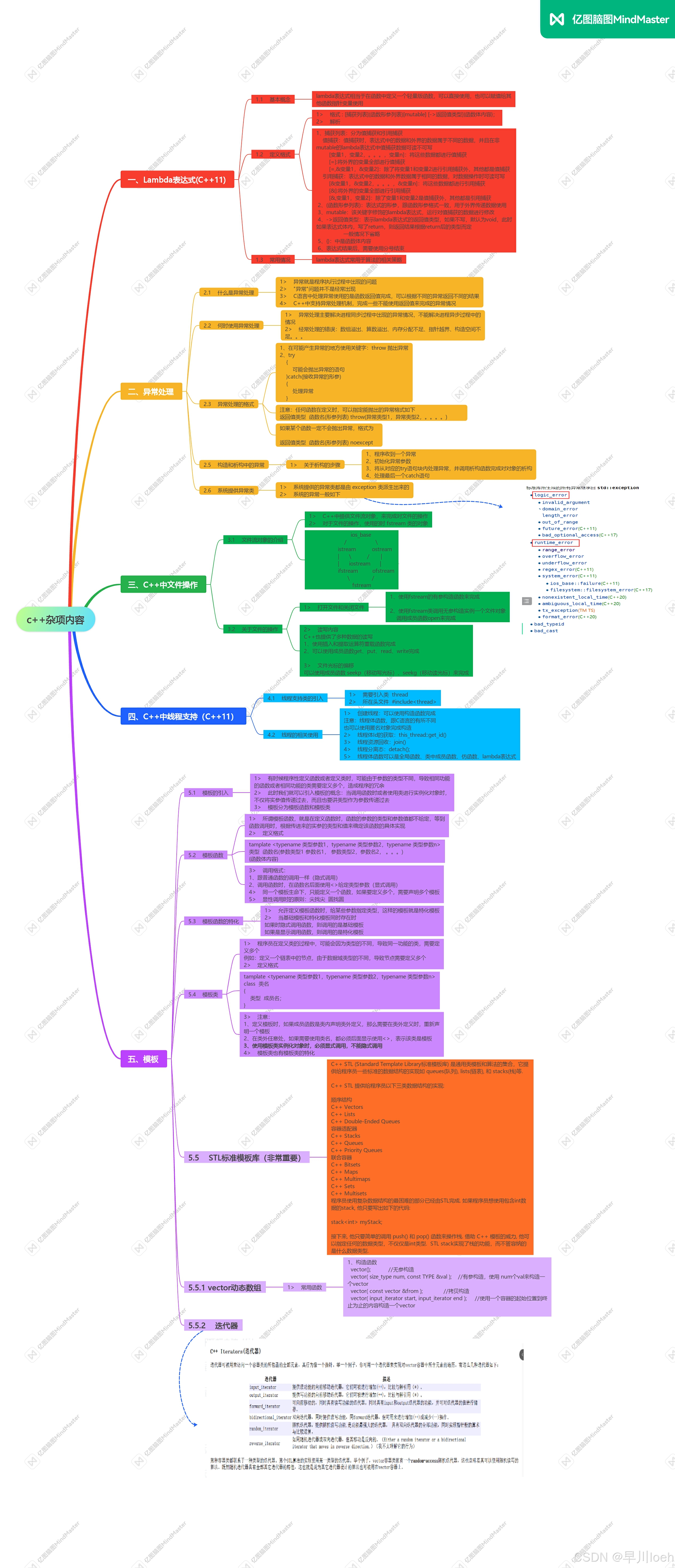
数模竞赛论文结构剖析

1. 摘要
2. 问题重述
3. 模型假设
4. 符号说明
5. 问题分析
6. 模型建立
7. 模型求解
8. 结果及分析
9. 检验与推广
10. 模型评价
11. 参考文献
12. 附录

摘要

摘要一般应包括：

1. 用一两句话说明原题中要求解决的问题
2. 明确说明建立了什么模型，在数学上属于什么类型，建模的思想，思路，模型特点
3. 算法思想，求解思路，特色；
4. 主要结果，数值结果，结论；
5. 模型优点，模型检验，灵敏度分析，有无改进、推广。

• 长度：不宜太短或太长，一页以内，包括上述要点，简洁达意非常重要
• 论文最重要的部分；要保证准确、简明、条理清晰，突出特色和创新点。
• 独立成文。
  注：数模竞赛评阅时一般会首先根据摘要和论文整体结构及概貌对论文优劣进行初步筛选，通常摘要也会单独赋分。
  

问题方法基本概述，对数据进行预处理，对问题解答的概述
提出建立…模型，描述…关系，基于…可知…结果
可以补充具体的算法和求解过程
模型优缺点，灵敏度分析，模型检验
总-分-总

问题重述

• 不是题目的完整复制，切记不能简单复制原题目
• 很多比赛对参赛论文都要进行查重，“问题重述”是雷区
• 根据自己的理解，用自己的语言清楚简明地阐述背景、条件和要求
• 问题重述部分有时也可以添加关于问题背景的描述

模型假设

• 假设要合理、全面，不要罗列大量无关紧要的假设，关键性假设不能缺，重要假设3-5条。
• 假设的提出：根据题目中条件作出假设；根据题目中的要求作出假设。
• 合理假设的作用：简化问题，明确问题，限定模型的适用范围，
• 假设一般是在做题过程中提出
• 为模型的改进和拓展做铺垫

符号说明

• 科学规范，全文通用，保持一致：

1. 尽可能用数学语言作为符号；
2. 避免混淆，如尽量不用数字作为上标等；
3. 尽可能不用英文单词作为数学符号；
4. 符号应是统一的，在全文任何地方表达的意思一致

• 可用列表的形式：排列工整，比如：符号，说明，单位等。
  

问题分析

• 概念解析、思路部析、方法介绍：

1. 对赛题中的一些专业术语或概态进行解析
2. 破解问题需采用的整体策略或思路，如思路图，解决方案等；
3. 论文中可能要采用的方法的介绍；
4. 其它相关的建模前的准备工作。

• 技术思路图，研究方案图，逻辑结构图，层次分析图等
• 不要做成摘要的重复。
  

模型的建立

• 模型的主要类型：
  数学规划、微分方程、差分方程、概率随机、统计预测、图论优化等；
  模型也可以是用来揭示事物发展规律的一种数学结构，比如热传导模型，扩散模型等

• 注意模型与算法的区别
  算法通常是指对于特定模型或问题的求解方法；
  比如数值计算法、最小二乘法、遗传算法、模拟退火、蚁群算法等。

• 模型建立过程中的几个要点：
  模型的整体设计，基于合理的假设，形成数学结构，明确数学表达式。

• 数学模型要明确、合理、简洁，具有一般性：
  有些论文不给出明确的模型，只是就赛题所给的特殊情况，用“凑”的方法给出结果，虽然结果基本正确，但缺乏一般性，不是数学建模的正确思路，不能描述事物规律性。

• 避免罗列一系列模型，又不作评价。

• 多模型：由易到难，由简单到复杂，由特殊到一般，分析条件、适应性、扩展性等。

多目标优化模型

模拟退火算法步骤

多模型结果对比

模型求解

• 算法设计或选择，算法思想依据；
• 算法的合理性分析；
• 明确给出算法流程图、步骤、虚拟代码等；
• 涉及到算法参数设置的，明确给出参数的取值及理由
• 分析算法对参数的敏感性，
• 多种算法求解，要注意分析比较
  算法虚拟代码
  

算法流程图

算法参数设置

结果表示、分析、检验

• 最终数值结果的正确性或合理性是第一位的。
• 结果表示：重要结果一目了然，直观展示，集中展示
  数值结果：有确定性答案的，要尽可能准确无误；
  结果表示：可以用表格、图示、加粗等形式；
  注重检验：对数值结果或模拟结果进行必要的检验；
  注重显现：可略夸张的展示与突出。

模型评价

• 优点可适当突出：
  模型上的优点，算法上的优点，模型的适用性、鲁棒性等。
• 缺点不回避：
  实事求是，避免假大空，如数据采集问题，模型假设上的
  问题，计算复杂度上的问题，结果的精度问题等。
• 优缺点：
  各总结2-3条。

参考文献

• 列出论文中确实应用了其中的方法或结论的文献；
• 正文中按从小到大依次标注文献序号；
• 科学规范引用
• 专著、论文、标准、专利、报纸等，电子文献（网页）也可以引用；
• 尽可能引用学术价值高、认可度高的文献，
• 有的赛区在报送国家奖论文时，没有规范引用和标注文献的论文不予报送
  

附录

• 论文中难以罗列的，详细的结果，详细的数据表格，可在此列出；
• 赛题重要的结果数据，应在正文中列出；
• 求解模型的计算程序：标注清楚什么软件、什么版本解决的哪个问题的程序；
• 附录中的数据、程序等，尽可能整理好，排版工整紧凑，不要截图贴图
  

数模竞赛论文写作技巧

标题的定制与使用

• 只读各级标题，就能知道整篇论文的概要。
• 多设置标题；避免大段大段的文字，不见一个标题，正文至少要设置两级标题，每一小节都有一个清晰的目的，一目了然。
• 一般也不要超过三级标题，如（1.1.1.1），三级标题以下可以用 (1)(2)(3)等序号来分层次表示
  

善用图表

• 一图胜干言，图形直观形象，一目了然；
• 图形要清晰，达意，明确，直观；
• 表格清晰，易于集中、对比；
• 图有图名、图序；表有表头、表序，如三线表；
• 图文并茂，文字、公式、图形、表格。
  

公式规范

• 用数学语言、数学符号进行组织
• 排列整齐，编序有致，
• 切忌编程语言与数学语言混淆；
• 模型尽可能用数学公式与结构进行呈现

突出算法模型和结果

论文评阅原则：

• 假设的合理性；
• 模型的创造性（合理性）
• 结果的正确性（算法的明确合理性）
• 表述的清晰性（论文整体清晰美观）

论文写作三忌

1. 忌在正文中直接贴程序代码，贴程序运行结果
2. 总大量截图贴图，为规避查重进行贴图；
3. 忌论文或支撑材料中出现参赛单位、队员等信息。

竞赛注意事项

• 及时保存，可以设置自动保存，数据、文献、代码、文本等；
• 多做备份，注意分清版本；在不同电脑里备份；
• 尽早动手写作，留足时间修改完善；
• 中途一般不更换选题；
• 三人同心，分工协作，基本保持同步

数模竞赛题目特点分析

数学建模竞赛赛题基本特点

• 开放性：较大灵活性，供参赛者发挥创造力
• 实际背景/时代特征（实用性/时代性/趣味性）：
  一定的亲和力/社会热点问题；激发思考；
• 综合性：开拓知识结构，不是单一数学问题；
• 基础性（可接受性）：少涉及专业知识；适中的数学知识
• 可区分性

赛题题型结构

1. 实际问题背景

• 涉及面宽，有社会，经济，管理，生活，环境，自然现象，工程技术，现代科学中出现的新问题等；
• 一般都有一个比较确切的现实问题

2. 若干基本条件（假设）
3. 要求回答的问题（多个）：

• 比较确定性的答案（基本答案）
• 更细致或更高层次的讨论结果提法和结果）；（往往是讨论最优方案的
• 有区分度的问题，比较开放的问题

数学建模赛题的常用方法

1. 机理分析法：
   根据对客观事物特性的认识从基本物理定律以及系统的结构数据来推导出模型
2. 数据分析法：
   通过对量测数据的统计分析，找出与数据拟合最好的模型

• 回归或分类分析法：用于对函数$f(x)$的一组观测值$(x_i,f_i),i=1,2,\dots ,n$，确定函数的表达式，由于处理的是静态的独立数据，故称为数理统计方法，通常结合机器学习

• 时序分析法：处理的是动态的相关数据，又称为过程统计方法

• 数据挖掘法：处理的是各种各样的数据，混杂数据、非线性数据、不确定数据、非结构化数据等。

3. 仿真和其他方法

选题技巧

• 赛题一般无难易之分
• 选择自己队伍里最合适的；拿到赛题后，先每位队员独立读题并查阅相关文献，进行深入思考，形成初步思路然后再讨论选哪个题目；题目都没读懂的情况下，去盲目选题，是不合适的；
• 不跟风式选题；
• “难题”（选题量少）往往更容易获奖
• 题目选定后，一般不再更换