前言:
今天我们要讲解的是数据结构中图的部分,这部分在我们实际生活中也是经常会碰到的,同时这部分也是数据结构中比较有难度的部分,这部分内容我会把它分为多章来进行讲解,今天我们先来讲解一下图的基本概念和存储结构
目录
一、图的基本概念
1. 图的定义
2. 术语解释
3. 图的分类
二、图的表示
1.邻接矩阵
2. 邻接表
三、总结
一、图的基本概念
1. 图的定义
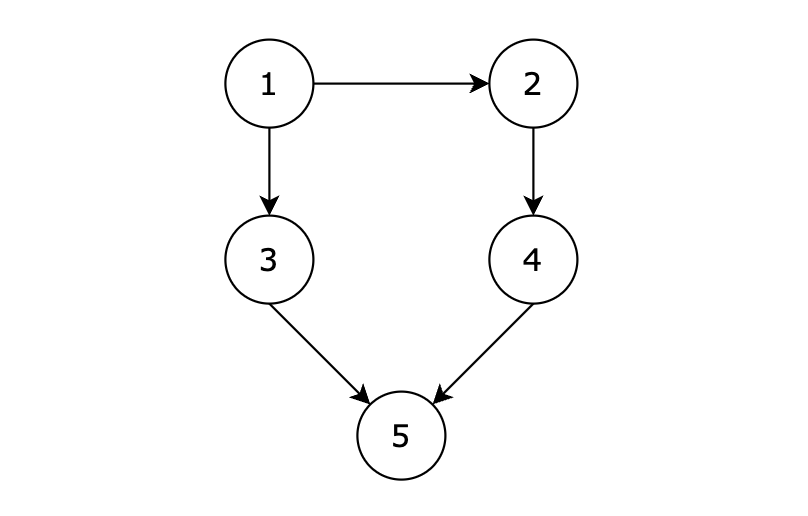
图是一种非线性的数据结构:G=(V,E),它由节点(也称为顶点)和连接这些节点的边组成。图可以用来表示现实世界中的各种关系,如社交网络、交通网络、电路网络等。

2. 术语解释
- 顶点(Vertex):图中的基本元素,可以表示任何实体,如人、地点、事物等。顶点集合V={x|x属于某个数据对象集}是有穷非空集合
- 边(Edge):连接两个顶点的线,表示顶点之间的关系。边的集合:E={(x,y)|x,y属于V}(无向图)或者E={<x,y>|x,y属于V&&Path(x,y)}是顶点间关系的有穷集合
- 邻接(Adjacent):如果两个顶点通过一条边直接相连,则称这两个顶点是邻接的。
- 度(Degree):对于无向图而言,一个顶点的度是指与该顶点相连的边的数量。但是对于有向图来说,一个顶点的度分为入度和出度,顶点的入度是以该顶点为终点的有向边的条数,出度则是以该顶点为起点的有向边的条数,顶点的度等于入度和出度之和
- 路径(Path):顶点序列,其中每对连续的顶点都是邻接的。
- 环(Cycle):路径中的第一个和最后一个顶点是同一个顶点的情况。
- 连通图:对于任意两个顶点,都存在一条路径连接它们,即图中每一个顶点都不是单独存在的,它们都可以通过各种路径互相到达(如果有顶点单独存在,没有与其它任意顶点相连,则称这个顶点为一个孤岛)
- 连通分量:一个图中的不连通部分。
3. 图的分类
-
无向图(Undirected Graph):连接两个顶点的边没有方向,没有方向意味着两个顶点是互相连通的,这种常见的如朋友关系图:我是你的好友,同样你也是我的好友

-
有向图(Directed Graph):边有方向,有方向意味着一个顶点可以到另一个顶点,但是反过来不行,这种关系常见的如网页链接图:我可以点击这个链接跳到一个图片,但是无法通过这个图片再跳回原来的界面。

-
简单图(Simple Graph):没有重复的边和自环(顶点连接到自身的边)。
-
多重图(Multigraph):允许有重复的边和自环。
-
带权图(Weighted Graph):每条边上都有权重,一般是数字,可以表示距离、成本等。比如,我们在修从杭州到西安的高铁时,我们可以选择经过郑州,也可以选择经过武汉,这就产生了不同的路径,我们可以比较两个路径的开支来选择经过哪个城市,这就是权值

二、图的表示
图的表示有以下三种方法:
1.邻接矩阵
- 邻接矩阵:使用二维数组来表示图,其中矩阵的元素表示顶点之间的连接情况,顶点之间的关系只有连通与不连通,所以我们可以用0和1来表示

注意:
1、无向图的邻接矩阵是对称的,但是有向图的邻接矩阵不一定对称
2、如果边上带权值,可以用权值来代替上面的0和1,相连通的顶点可以用权值来表示,不连通的可以用无穷来表示

3、邻接矩阵的有点是可以直观的看出两个顶点之间是否相连,但是当顶点过多、边过少的时候,就会存储大量的0,就会很不方便
代码实现:
#include<iostream>
#include<vector>
#include<string>
#include<map>
template<class V, class W, W MAX_W = INT_MAX, bool Direction = false>
class Graph
{
public:
typedef Graph<V, W, MAX_W, Direction> Self;
Graph() = default;
Graph(const V* vertexs, size_t n)
{
_vertexs.reserve(n);
for (size_t i = 0; i < n; ++i)
{
_vertexs.push_back(vertexs[i]);
_vIndexMap[vertexs[i]] = i;
}
// MAX_W 作为不存在边的标识值
_matrix.resize(n);
for (auto& e : _matrix)
{
e.resize(n, MAX_W);
}
}
size_t GetVertexIndex(const V& v)
{
auto ret = _vIndexMap.find(v);
if (ret != _vIndexMap.end())
{
return ret->second;
}
else
{
throw invalid_argument("不存在的顶点");
return -1;
}
}
void _AddEdge(size_t srci, size_t dsti, const W& w)
{
_matrix[srci][dsti] = w;
if (Direction == false)
{
_matrix[dsti][srci] = w;
}
}
void AddEdge(const V& src, const V& dst, const W& w)
{
size_t srci = GetVertexIndex(src);
size_t dsti = GetVertexIndex(dst);
_AddEdge(srci, dsti, w);
}
void Print()
{
// 打印顶点和下标映射关系
for (size_t i = 0; i < _vertexs.size(); ++i)
{
cout << _vertexs[i] << "-" << i << " ";
}
cout << endl << endl;
cout << " ";
for (size_t i = 0; i < _vertexs.size(); ++i)
{
cout << i << " ";
}
cout << endl;
// 打印矩阵
for (size_t i = 0; i < _matrix.size(); ++i)
{
cout << i << " ";
for (size_t j = 0; j < _matrix[i].size(); ++j)
{
if (_matrix[i][j] != MAX_W)
cout << _matrix[i][j] << " ";
else
cout << "#" << " ";
}
cout << endl;
}
cout << endl << endl;
// 打印所有的边
for (size_t i = 0; i < _matrix.size(); ++i)
{
for (size_t j = 0; j < _matrix[i].size(); ++j)
{
if (i < j && _matrix[i][j] != MAX_W)
{
cout << _vertexs[i] << "-" << _vertexs[j] << ":" <<
_matrix[i][j] << endl;
}
}
}
}
private:
map<V, size_t> _vIndexMap;
vector<V> _vertexs; // 顶点集合
vector<vector<W>> _matrix; //存储边集合的矩阵
};
void TestGraph()
{
Graph<char, int, INT_MAX, true> g("0123", 4);
g.AddEdge('0', '1', 1);
g.AddEdge('0', '3', 4);
g.AddEdge('1', '3', 2);
g.AddEdge('1', '2', 9);
g.AddEdge('2', '3', 8);
g.AddEdge('2', '1', 5);
g.AddEdge('2', '0', 3);
g.AddEdge('3', '2', 6);
g.Print();
}
int main()
{
TestGraph();
return 0;
}运行结果:

2. 邻接表
- 邻接表:使用列表来表示图,每个顶点对应一个列表,列表中包含所有与该顶点相连的顶点。


-
template<class W> struct LinkEdge { int _srcIndex; int _dstIndex; W _w; LinkEdge<W>* _next; LinkEdge(const W& w) : _srcIndex(-1) , _dstIndex(-1) , _w(w) , _next(nullptr) {} }; template<class V, class W, bool Direction = false> class Graph { typedef LinkEdge<W> Edge; public: Graph(const V* vertexs, size_t n) { _vertexs.reserve(n); for (size_t i = 0; i < n; ++i) { _vertexs.push_back(vertexs[i]); _vIndexMap[vertexs[i]] = i; } _linkTable.resize(n, nullptr); } size_t GetVertexIndex(const V& v) { auto ret = _vIndexMap.find(v); if (ret != _vIndexMap.end()) { return ret->second; } else { throw invalid_argument("不存在的顶点"); return -1; } } void AddEdge(const V& src, const V& dst, const W& w) { size_t srcindex = GetVertexIndex(src); size_t dstindex = GetVertexIndex(dst); // 0 1 Edge* sd_edge = new Edge(w); sd_edge->_srcIndex = srcindex; sd_edge->_dstIndex = dstindex; sd_edge->_next = _linkTable[srcindex]; _linkTable[srcindex] = sd_edge; // 1 0 // 无向图 if (Direction == false) { Edge* ds_edge = new Edge(w); ds_edge->_srcIndex = dstindex; ds_edge->_dstIndex = srcindex; ds_edge->_next = _linkTable[dstindex]; _linkTable[dstindex] = ds_edge; } } private: map<string, int> _vIndexMap; vector<V> _vertexs; // 顶点集合 vector<Edge*> _linkTable; // 边的集合的临接表 }; void TestGraph() { string a[] = { "张三", "李四", "王五", "赵六" }; Graph<string, int> g1(a, 4); g1.AddEdge("张三", "李四", 100); g1.AddEdge("张三", "王五", 200); g1.AddEdge("王五", "赵六", 30); } - 边列表:使用列表来存储图中的所有边,每条边由两个顶点表示。(这个不常用,在这里不做过多解释,想要了解的可以自行搜索一下)
三、总结
这篇讲的还是图的基本内容,后面我们会讲解图的广度和深度遍历,以及与图有关的算法

感谢各位大佬观看,创作不易,还望各位大佬点赞支持!!!