---

题目链接

点我 (^_^)

---

题目大意

---

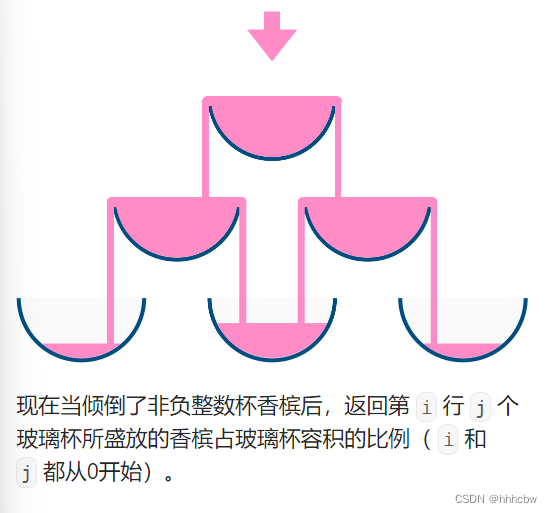
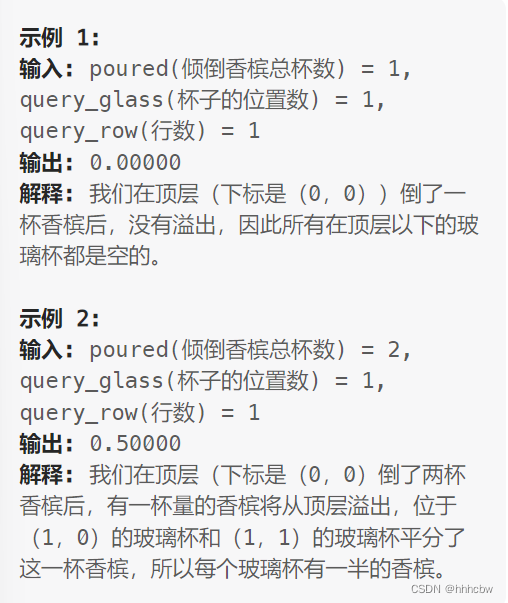
解题思路

一开始看到这个 poured 范围这么大，以为是可以直接推出数学公式，但推了半天没推出来。

然后发现，直接从顶部开始模拟即可，某个row 下的某个 glass 的体积等于其上面两个glass 的体积 - 1 相加再除2，可以写成如下公式：

$V_{row}^{glass}=(V_{row-1}^{glass-1}-1)/2+(V_{row-1}^{glass}-1)/2$

当然对于最外面的两个杯子的体积，只和其上面一个杯子的体积有关。 最后结果注意要和 1 取最小值。

当然，算法既可以写成递归形式，也可以写成递推形式，递归形式要使用记忆化搜索，否则会超时。

---

代码(C++)

递推

class Solution {
public:
    double champagneTower(int poured, int query_row, int query_glass) {
        vector<double> row = {(double)poured};
        for (int i = 1; i <= query_row; i++) {
            vector<double> nextRow(i + 1, 0.0);
            for (int j = 0; j < row.size(); j++) {
                double volume = row[j];
                if (volume > 1) {
                    nextRow[j] += (volume - 1) / 2;
                    nextRow[j + 1] += (volume - 1) / 2;
                }
            }
            row = nextRow;
        }            
        return min(1.0, row[query_glass]);
    }
};

递归

class Solution {
public:
    double dp[105][105];
    double eps = 0.000000001;
    double func(double poured, int query_row, int query_glass) {
        if (query_row == 0)
            return poured;
        if(dp[query_row][query_glass] != -1)
            return dp[query_row][query_glass];
        if(query_glass == 0)
            return dp[query_row][query_glass] = max(0.0, (func(poured, query_row-1, 0)-1) / 2);
        if(query_glass == query_row)
            return dp[query_row][query_glass] = max(0.0, (func(poured, query_row-1, query_glass-1)-1) / 2);
        return dp[query_row][query_glass] = max(0.0, (func(poured, query_row-1, query_glass-1)-1) / 2) + max(0.0, (func(poured, query_row-1, query_glass)-1) / 2);
    }

    double champagneTower(int poured, int query_row, int query_glass) {
        for(int i=0; i<100; ++i)
            for(int j=0; j<=i; ++j)
                dp[i][j] = -1;
        return min(1.0, func((double)poured, query_row, query_glass));
    }
};