【python计算机视觉编程——4.照相机模型与增强现实】

python计算机视觉编程——4.照相机模型与增强现实

4.照相机模型与增强现实
- 4.1 真空照相机模型
- - 4.1.1 照相机矩阵
  - 4.1.2 三维点的投影
  - 4.1.3 照相机矩阵的分解
  - 4.1.4 计算照相机中心
- 4.2 照相机标定
- 4.3 以平面和标记物进行姿态估计
- sift.py
- homography.py
- 主函数
- homography.py
- camera.py
- 主函数
- 4.4 增强现实
- - 4.4.1 PyGame和PyOpenGL
  - 4.4.2 从照相机矩阵到OpenGL格式
  - 4.4.3 在图像中放置虚拟物体
  - 4.4.4 综合集成

4.照相机模型与增强现实

4.1 真空照相机模型

在针孔照相机中，三维点X投影为图像点x（两个点都是用齐次坐标表示的），如下所示：
$\lambda{\bf x=PX}$
${\bf P}$ 为3×4的照相机矩阵，在齐次坐标系中，三维点 ${\bf X}$ 的坐标由4个元素组成 ${\bf X}=[X,Y,Z,W]$ ， $\lambda$ 是三维点的逆深度

4.1.1 照相机矩阵

在这里插入图片描述

照相机矩阵可分解为
${\bf P}=K[{\bf R}|t]$
${\bf R}$ 是描述照相机方向的旋转矩阵；t是描述照相机中心位置的三维平移向量；K是内标定矩阵，描述的是照相机的投影性质。其中K也可以称为内参矩阵， $[{\bf R}| t]$ 为外参矩阵

内参：
- 焦距：相机镜头的焦距，影响图像的放大倍率。
- 主点：图像平面上光轴与图像平面的交点。
- 畸变参数：描述镜头引起的几何畸变（如径向畸变和切向畸变）。
外参：
- 旋转矩阵：描述相机坐标系相对于世界坐标系的旋转。
- 平移向量：描述相机坐标系原点相对于世界坐标系的平移。

内标定矩阵K的格式如下：
$\begin{pmatrix} f_x & s & c_x\\ 0 & f_y & c_y \\ 0 & 0 & 1\end{pmatrix}$

$f_x$ 和 $f_y$ ：分别是x轴和y轴的焦距（以像素为单位）。这些值表示相机在水平和垂直方向上的放大比例。
s：是相机的切向畸变系数，表示 x 轴和 y 轴之间的非正方形性（通常在大多数相机中为 0）。
$c_x$ 和 $c_y$ ：主点（或光轴交点）的坐标，表示图像中心的像素坐标。
1：齐次坐标的缩放因子。

4.1.2 三维点的投影

from scipy.linalg import expm
import numpy as np 
from pylab import *

class Camera(object):
    def __init__(self,P):
        self.P=P      #照相机矩阵
        self.K=None   #标定矩阵
        self.R=None   #旋转矩阵
        self.t=None   #平移向量
        self.c=None   ##照相机中心
    def project(self,X):
        x=np.dot(self.P,X)  #得到一个包含齐次坐标的投影结果 x
        for i in range(3):
            x[i]/=x[2]  # 以实现归一化。
        return x

points=loadtxt('house.p3d').T  # 对加载的数据进行转置，使得每一列代表一个三维点（即，每一列是 [x, y, z]）。


#  ones(points.shape[1])：创建一个与点数相同的全 1 数组，表示齐次坐标中的最后一维。
#  vstack(...)：将这些 1 堆叠到三维点数据的底部，转换为齐次坐标形式（即 [x, y, z, 1]）
points=vstack((points,ones(points.shape[1])))
# print(points)

# 将单位矩阵和列向量水平堆叠，得到一个 3x4 的投影矩阵 P。
# 这个矩阵表示一个简单的投影模型，平移向量使得相机位置位于 z = -10 的位置。
P=hstack((eye(3),array([[0],[0],[-10]]))) # eye(3)为单位矩阵
# print(P)
cam=Camera(P)
x=cam.project(points)

figure()
plot(x[0],x[1],'k.')
show()

在这里插入图片描述

def rotation_matrix(a):  #根据向量 a 生成一个 4x4 的旋转矩阵。
#   其中左上角的 3x3 部分表示旋转，其他部分是齐次坐标系统的扩展。
    R=eye(4)
    R[:3,:3]=expm([[0,-a[2],a[1]],
                   [a[2],0,-a[0]],
                   [-a[1],a[0],0]])  #这个矩阵用于表示叉积的线性变换，可以通过矩阵指数运算得到旋转矩阵。
    return R

r=0.05*np.random.rand(3)  #将这个随机数组的每个元素都乘以 0.05，以得到一个较小的随机旋转向量 r
rot=rotation_matrix(r)
figure()
for t in range(20):
    cam.P=dot(cam.P,rot)
    x=cam.project(points)
    plot(x[0],x[1],'k.')

在这里插入图片描述

首先生成一个小的随机旋转向量，并计算出对应的 4x4 旋转矩阵。
然后创建一个新的图形窗口，并在一个循环中，通过不断旋转相机的投影矩阵来更新视图。
最后，将投影后的 3D 点绘制在图形窗口中，形成一个动态的图像。

4.1.3 照相机矩阵的分解

将factor方法添加到Camera类中，里面需要用到sign函数
$\begin{cases} 1, & x > 0 \\ 0, & x=0 \\ -1, & x<0 \\ \end{cases}$

def factor(self):
    K,R=linalg.rq(self.P[:,:3]) # 将照相机矩阵 P 的左上 3x3 部分分解为上三角矩阵 K 和正交矩阵 R
        
        
#       diag():如果是矩阵，则提取对角线元素，形成一个一维数组。
#              如果是一维数组，则将一维数组的元素形成对角矩阵。
#       sign():应用 sign 函数
    T=diag(sign(diag(K)))  # 构造对角矩阵 T，其对角线元素为 K 对角线元素的符号。
    if linalg.det(T)<0:  # 检查 T 的行列式是否为负。如果是，则调整 T 使得行列式为正。
        T[1,1]*=-1
        self.K=dot(K,T)
        self.R=dot(T,R)
        self.t=dot(linalg.inv(self.K),self.P[:,3])  # linalg.inv(self.K)用于计算标定矩阵 K 的逆矩阵
    return self.K,self.R,self.t

T的行列式为正的原因：因为在实际应用中，我们通常希望标定矩阵 K 的对角线元素（表示焦距和其他内部参数）都是正的，以符合实际的物理意义。

K=array([[1000,0,500],
         [0,1000,300],
         [0,0,1]])# 3x3 的相机内参矩阵，通常包括焦距和主点坐标。
tmp=rotation_matrix([0,0,1])[:3,:3]  # 计算一个绕 z 轴旋转的 3x3 旋转矩阵 tmp
Rt=hstack((tmp,array([[50],[40],[30]])))  # 将旋转矩阵 tmp 和一个平移向量 array([[50], [40], [30]]) 组合成一个 3x4 的矩阵 Rt。
cam=Camera(dot(K,Rt))

print(K)
print(Rt)
print('----')
print(cam.factor())

在这里插入图片描述

4.1.4 计算照相机中心

给定照相机投影矩阵P，我们可以计算出空间上照相机的所在位置。照相机的中心C，是一个三维点，满足约束 ${\bf PC}=0$ 。对于投影矩阵为 ${\bf P}=K[{\bf R}|t]$ 的照相机，有：
$K[{\bf R}|t]{\bf C}=K{\bf R}{\bf C}+Kt=0$
照相机的中心可以由下述式子来计算
$C=-R^Tt$
将center函数添加到Camera类中

def center(self):
    # 首先检查 self.c 是否已经被计算过。
    # 如果 self.c 不为 None，则直接返回已计算的相机中心 self.c，以避免重复计算
    if self.c is not None:
        return self.c
    else:
        self.factor()
        self.c=-dot(self.R.T,self.t)  # 将平移向量转化为相机坐标系原点在世界坐标系中的位置
        return self.c

K=array([[1000,0,500],
         [0,1000,300],
         [0,0,1]])# 3x3 的相机内参矩阵，通常包括焦距和主点坐标。
tmp=rotation_matrix([0,0,1])[:3,:3]  # 计算一个绕 z 轴旋转的 3x3 旋转矩阵 tmp
Rt=hstack((tmp,array([[50],[40],[30]])))  # 将旋转矩阵 tmp 和一个平移向量 array([[50], [40], [30]]) 组合成一个 3x4 的矩阵 Rt。
cam=Camera(dot(K,Rt))
camera_center = cam.center()
print("相机中心位置:", camera_center)

在这里插入图片描述

4.2 照相机标定

相机标定旨在确定相机的内参和外参，从而实现准确的图像分析和三维重建。

具体操作步骤：
1. 测量你选定矩形标定物体的边长 ${\rm d}X$ 和 ${\rm d}Y$
2. 将照相机和标定物体放置在平面上，使得照相机的背面和标定物体平行，同时物体位于照相机图像视图的中心，你可能需要调整照相机或者物体来获得良好的对齐效果
3. 测量标定物体到照相机的距离 ${\rm d}Z$
4. 拍摄一副图像来检验该设置是否正确，即标定物体的边要和图像的行和列对齐
5. 使用像素数来测量标定物体图像的宽度和高度 ${\rm d}x$ 和 ${\rm d}y$ 。

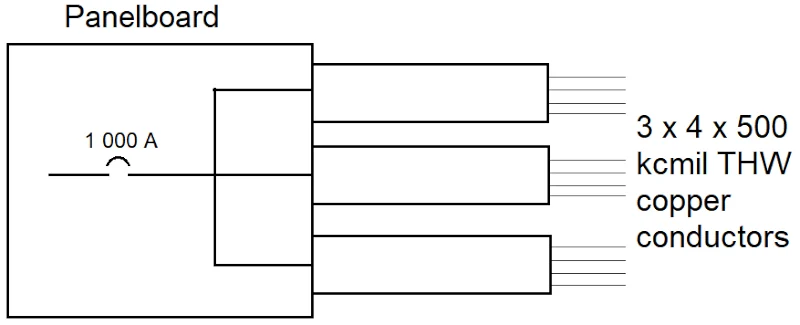
实验设置情况如图所示。现在，使用下面的相似三角形（参见图4-1）关系可以获得焦距：
$f_x=\frac{{\rm d}x}{{\rm d}X}{\rm d}Z,f_y=\frac{{\rm d}y}{{\rm d}Y}{\rm d}Z$
在这里插入图片描述

可以获取到 ${\rm d}X=130,{\rm d}Y=185$ （即物体的宽度和高度）， ${\rm d}Z=460$ （即照相机到物体的距离）， ${\rm d}x=722,{\rm d}y=1040$ （即物体的宽度和高度所占的像素值），可以用如下方法进行获取物体的宽和高，取一个近似值，这里就按课本的值进行计算

import cv2
import matplotlib.pyplot as plt

# 定义回调函数，用于处理点击事件
def click_event(event, x, y, flags, params):
    if event == cv2.EVENT_LBUTTONDOWN:
        # 在图像上绘制一个小圆圈来标记点击位置
        cv2.circle(image, (x, y), 5, (0, 255, 0), -1)
        # 显示点击位置的坐标
        print(f"Clicked at (x, y): ({x}, {y})")
        # 在图像上显示点击坐标
        cv2.putText(image, f"({x}, {y})", (x, y), cv2.FONT_HERSHEY_SIMPLEX, 2, (255, 255, 255), 2)
        # 更新窗口显示
        cv2.imshow("Image", image)

# 读取图像
image_path = 'calibration.jpg'
image = cv2.imread(image_path)
# 创建一个窗口，设置为自动调整大小
cv2.namedWindow('Image', cv2.WINDOW_NORMAL)

# 创建一个窗口来显示图像
cv2.imshow("Image", image)

# 设置回调函数以处理鼠标点击事件
cv2.setMouseCallback("Image", click_event)

# 等待用户点击
cv2.waitKey(0)
cv2.destroyAllWindows()

在这里插入图片描述

所以可以计算出焦距
$f_x=\frac{722}{130}460≈2555,f_x=\frac{1040}{185}460≈2586$
最后还需求出图片所占的像素数

在这里插入图片描述

写入如下辅助函数中

def my_calibration(sz):   #输入参数为表示图像大小的元组
    row,col=sz
    fx=2555*col/2592
    fy=2586*row/1936
    K=diag([fx,fy,1])
    K[0,2]=0.5*col
    K[1,2]=0.5*row
    return K

4.3 以平面和标记物进行姿态估计

这时候我们需要借助之前几章学过的函数（为了方便学习，我重新复制了过来，尽可能对这些函数的使用更加熟悉，后期是可以封装成py文件进行调用）

sift.py

import os

def process_image(imagename, resultname, params="--edge-thresh 10 --peak-thresh 5"):
    if imagename[-3:] != 'pgm':
        im = Image.open(imagename).convert('L')
        im.save('tmp.pgm')
        imagename = 'tmp.pgm'
        
    cmmd = str(".\sift.exe " + imagename + " --output=" + resultname + " " + params)
    os.system(cmmd)
    print('processed', imagename, 'to', resultname)

def read_features_from_file(filename):
    f=loadtxt(filename)
    return f[:,:4],f[:,4:]

def match(desc1,desc2):
    desc1=array([d/linalg.norm(d) for d in desc1])
    desc2=array([d/linalg.norm(d) for d in desc2])
    dist_ratio=0.6
    desc1_size=desc1.shape
    matchscores=zeros((desc1_size[0],1),'int')
    desc2t=desc2.T
    for i in range(desc1_size[0]):
        dotprods=dot(desc1[i,:],desc2t)
        dotprods=0.9999*dotprods
        indx=argsort(arccos(dotprods))
        if arccos(dotprods)[indx[0]]<dist_ratio*arccos(dotprods)[indx[1]]:
            matchscores[i]=int(indx[0])
    return matchscores

def match_twosided(desc1,desc2):
    matches_12=match(desc1,desc2)
#     print(matches_12.shape)
    matches_21=match(desc2,desc1)
    ndx_12=matches_12.nonzero()[0] #获取的是与desc2匹配的desc1的索引值
    for n in ndx_12:
        if matches_21[int(matches_12[n])]!=n:  # matches_12[n]是desc1中第n个描述符在desc2中的匹配索引
            matches_12[n]=0
    return matches_12

homography.py

def make_homog(points): 
    return np.vstack((points,np.ones((1,points.shape[1]))))

def H_from_points(fp,tp):
    if fp.shape!=tp.shape: # 确保源点 (fp) 和目标点 (tp) 的形状相同。如果形状不匹配，抛出异常。
        raise RuntimeError('number of points do not match')
    # 归一化源点:计算源点的均值m和标准差maxstd。创建归一化矩阵C1，用于将源点fp进行归一化处理，以减小计算中的数值误差。
    m=np.mean(fp[:2],axis=1)  # 计算源点的均值 m，对每个坐标分量进行均值计算
    maxstd=max(np.std(fp[:2],axis=1))+1e-9    # 计算源点的标准差 maxstd，加一个小偏移量以避免除零错误  
    C1=np.diag([1/maxstd,1/maxstd,1])   # 创建归一化矩阵 C1，用于缩放坐标
    C1[0][2]=-m[0]/maxstd  # 设置 C1 矩阵的平移部分
    C1[1][2]=-m[1]/maxstd  # 设置 C1 矩阵的平移部分
    fp=np.dot(C1,fp)       # 应用归一化矩阵 C1 到源点 fp
        
        
    # 归一化目标点:类似地，对目标点进行归一化处理，计算均值和标准差，并应用归一化矩阵 C2。
    m=np.mean(tp[:2],axis=1)
    maxstd=max(np.std(tp[:2],axis=1))+1e-9
    C2=np.diag([1/maxstd,1/maxstd,1])
    C2[0][2]=-m[0]/maxstd
    C2[1][2]=-m[1]/maxstd
    tp=np.dot(C2,tp)
        
        
    nbr_correspondences=fp.shape[1]
    A=np.zeros((2*nbr_correspondences,9)) #构建矩阵A，用于求解单应性矩阵。每对点提供两个方程，总共 2 * nbr_correspondences 行。
    for i in range(nbr_correspondences):
        A[2*i]=[-fp[0][i],-fp[1][i],-1,0,0,0,
                tp[0][i]*fp[0][i],tp[0][i]*fp[1][i],tp[0][i]]
        A[2*i+1]=[0,0,0,-fp[0][i],-fp[1][i],-1,
                    tp[1][i]*fp[0][i],tp[1][i]*fp[1][i],tp[1][i]]
    U,S,V=np.linalg.svd(A) # 使用奇异值分解 (SVD)求解矩阵A的最小特征值对应的向量。取V的最后一行（对应于最小特征值），重塑为3x3矩阵 H
    H=V[8].reshape((3,3))
#     反归一化
    H=np.dot(np.linalg.inv(C2),np.dot(H,C1))# 使用逆归一化矩阵将计算得到的单应性矩阵从归一化坐标系转换回原始坐标系，并进行归一化处理。
#     归一化，然后返回
    return H/H[2,2]

class RansacModel(object):
    """ 用于测试单应性矩阵的类，其中单应性矩阵是由网站 http://www.scipy.org/Cookbook/RANSAC 上
    的 ransac.py 计算出来的
    """

    def __init__(self,debug=False):
        self.debug=debug 
    def fit(self,data):

        """ 计算选取的 4 个对应的单应性矩阵 """
        # 将其转置，来调用 H_from_points() 计算单应性矩阵
        data = data.T
        # 映射的起始点
        fp = data[:3,:4]
        # 映射的目标点
        tp = data[3:,:4]
        # 计算单应性矩阵，然后返回
        return H_from_points(fp,tp)

    def get_error(self, data, H):
        """ 对所有的对应计算单应性矩阵，然后对每个变换后的点，返回相应的误差 """
        data = data.T
        # 映射的起始点
        fp = data[:3]
        # 映射的目标点
        tp = data[3:]
        
        # 变换fp
        fp_transformed = dot(H,fp)
        
        # 归一化齐次坐标
        for i in range(3):
            fp_transformed[i]/=fp_transformed[2]

        # 返回每个点的误差
        return sqrt( sum((tp-fp_transformed)**2,axis=0) )

def random_partition(n,n_data):
    """return n random rows of data (and also the other len(data)-n rows)"""
    all_idxs = np.arange( n_data )
    np.random.shuffle(all_idxs)
    idxs1 = all_idxs[:n]
    idxs2 = all_idxs[n:]
    return idxs1, idxs2

def ransac(data, model, n, k, t, d, debug=False, return_all=False):
    iterations = 0
    bestfit = None
    besterr = np.inf
    best_inlier_idxs = None
    while iterations < k:
        maybe_idxs, test_idxs = random_partition(n, data.shape[0])
        maybeinliers = data[maybe_idxs, :]
        test_points = data[test_idxs]
        maybemodel = model.fit(maybeinliers)
        test_err = model.get_error(test_points, maybemodel)
        also_idxs = test_idxs[test_err < t]  # select indices of rows with accepted points
        alsoinliers = data[also_idxs, :]
        if debug:
            print('test_err.min()', test_err.min())
            print('test_err.max()', test_err.max())
            print('numpy.mean(test_err)', np.mean(test_err))
            print('iteration %d:len(alsoinliers) = %d' %(iterations, len(alsoinliers)))
        if len(alsoinliers) > d:
            betterdata = np.concatenate((maybeinliers, alsoinliers))
            bettermodel = model.fit(betterdata)
            better_errs = model.get_error(betterdata, bettermodel)#重新计算总的error
            thiserr = np.mean(better_errs)
            if thiserr < besterr:
                bestfit = bettermodel
                besterr = thiserr
                best_inlier_idxs = np.concatenate((maybe_idxs, also_idxs))
        iterations += 1
    if bestfit is None:
        raise ValueError("did not meet fit acceptance criteria")
    if return_all:
        return bestfit, {'inliers': best_inlier_idxs}
    else:
        return bestfit

def H_from_ransac(fp,tp,model,maxiter=1000,match_theshold=10):
    # 对应点组
    data = vstack((fp,tp))
    # 计算 H，并返回
    H,ransac_data = ransac(data.T,model,4,maxiter,match_theshold,10,return_all=True)
#     print(H,ransac_data)
    return H,ransac_data['inliers']

主函数

使用RANSAC算法稳健地估计单应性矩阵

process_image('book_frontal.JPG','im0.sift')

#回顾一下:l0(前四列)是兴趣点的坐标、尺度和方向角度,d0(后128列)是用整数数值表示的描述子
l0,d0=read_features_from_file('im0.sift')

process_image('book_perspective.JPG','im1.sift')
l1,d1=read_features_from_file('im1.sift')

matches=match_twosided(d0,d1)
ndx=matches.nonzero()[0]  # 找到所有匹配的特征点的索引。
fp=make_homog(l0[ndx,:2].T)  # 将特征点转换为齐次坐标的函数。转置完后相当于一列一个特征点的坐标,然后在最后一行添加1(转为齐次坐标)
ndx2=[int(matches[i]) for i in ndx]
tp=make_homog(l1[ndx2,:2].T)

model=RansacModel()
H=H_from_ransac(fp,tp,model)[0]   #H矩阵表示如何把坐标点fp映射到坐标点tp上

我们需要将一些简单的三维物体放置在标记物上，这里我们使用下列函数产生一个立方体

def cube_points(c,wid):   # 用于生成一个立方体的顶点坐标。立方体的中心点为 c，边长的一半为 wid
    p=[]
#     底部
# 添加立方体底部的四个顶点。由于立方体的底部是平面，顶点在这个平面上，因此 z 坐标相同。
    p.append([c[0]-wid,c[1]-wid,c[2]-wid])
    p.append([c[0]-wid,c[1]+wid,c[2]-wid])
    p.append([c[0]+wid,c[1]+wid,c[2]-wid])
    p.append([c[0]+wid,c[1]-wid,c[2]-wid])
    p.append([c[0]-wid,c[1]-wid,c[2]-wid])
#     顶部
# 添加立方体顶部的四个顶点。与底部顶点不同的是，这些顶点的 z 坐标增加了 wid。
    p.append([c[0]-wid,c[1]-wid,c[2]+wid])
    p.append([c[0]-wid,c[1]+wid,c[2]+wid])
    p.append([c[0]+wid,c[1]+wid,c[2]+wid])
    p.append([c[0]+wid,c[1]-wid,c[2]+wid])
    p.append([c[0]-wid,c[1]-wid,c[2]+wid])
    
#     竖直边
# 添加立方体的竖直边的顶点。这里添加了从底部到顶部的边连接的所有点。
    p.append([c[0]-wid,c[1]-wid,c[2]+wid])
    p.append([c[0]-wid,c[1]+wid,c[2]+wid])
    p.append([c[0]-wid,c[1]+wid,c[2]-wid])
    p.append([c[0]+wid,c[1]+wid,c[2]-wid])
    p.append([c[0]+wid,c[1]+wid,c[2]+wid])
    p.append([c[0]+wid,c[1]-wid,c[2]+wid])
    p.append([c[0]+wid,c[1]-wid,c[2]-wid])
    
    return array(p).T

# 以c=[0,0,0.1]，wid=0.1为例
box=cube_points([0,0,0.1],0.1)
print(box.T)   # 为了方便查看，我把它转置了回去，不然最终每一列代表的是一个坐标
print(box.shape)   #  (3, 18)

在这里插入图片描述

有了单应性矩阵和照相机的标定矩阵，我们现在可以得出两个视图间的相对变换，此时我们还需要如下几个函数

homography.py

def normalize(points):
    points=points.astype(float)
    for row in points:
#         print(row)
        row/=points[-1]
    return points

camera.py

class Camera(object):
    def __init__(self,P):
        self.P=P      #照相机矩阵
        self.K=None   #标定矩阵
        self.R=None   #旋转矩阵
        self.t=None   #平移向量
        self.c=None   #照相机中心
    def project(self,X):
        x=np.dot(self.P,X)  #得到一个包含齐次坐标的投影结果 x
        for i in range(3):
            x[i]/=x[2]  # 以实现归一化。
        return x
    def factor(self):
        K,R=linalg.rq(self.P[:,:3]) # 将照相机矩阵 P 的左上 3x3 部分分解为上三角矩阵 K 和正交矩阵 R
        
        
#       diag():如果是矩阵，则提取对角线元素，形成一个一维数组。
#              如果是一维数组，则将一维数组的元素形成对角矩阵。
        T=diag(sign(diag(K)))  # 构造对角矩阵 T，其对角线元素为 K 对角线元素的符号。
        if linalg.det(T)<0:  # 检查 T 的行列式是否为负。如果是，则调整 T 使得行列式为正。
#             因为在实际应用中，我们通常希望标定矩阵 K 的对角线元素（表示焦距和其他内部参数）都是正的，以符合实际的物理意义。
            T[1,1]*=-1
            self.K=dot(K,T)
            self.R=dot(T,R)
            self.t=dot(linalg.inv(self.K),self.P[:,3])  # linalg.inv(self.K)用于计算标定矩阵 K 的逆矩阵
        return self.K,self.R,self.t
    def center(self):
# 首先检查 self.c 是否已经被计算过。
# 如果 self.c 不为 None，则直接返回已计算的相机中心 self.c，以避免重复计算
        if self.c is not None:
            return self.c
        else:
            self.factor()
            self.c=-dot(self.R.T,self.t)  # 将平移向量转化为相机坐标系原点在世界坐标系中的位置
            return self.c

主函数

通过调节元组(747,1000)改变图像的焦距（中心点）

K=my_calibration((747,1000))

box=cube_points([0,0,0.1],0.1)

cam1=Camera(hstack((K,dot(K,array([[0],[0],[-1]])))))
box_cam1=cam1.project(make_homog(box[:,:5]))

# print(H)
# print(box_cam1.shape)
box_trans=normalize(dot(H,box_cam1))

cam2=Camera(dot(H,cam1.P))
A=dot(linalg.inv(K),cam2.P[:,:3])
A=array([A[:,0],A[:,1],cross(A[:,0],A[:,1])]).T
cam2.P[:,:3]=dot(K,A)

box_cam2=cam2.project(make_homog(box))

point=array([1,1,0,1]).T
print(normalize(dot(dot(H,cam1.P),point)))
print(cam2.project(point))

im0=array(Image.open('book_frontal.JPG'))
im1=array(Image.open('book_perspective.JPG'))

figure()
subplot(121)
imshow(im0)
plot(box_cam1[0,:],box_cam1[1,:],linewidth=3)

# figure()
subplot(122)
imshow(im1)
plot(box_trans[0,:],box_trans[1,:],linewidth=3)

figure()
imshow(im1)
plot(box_cam2[0,:],box_cam2[1,:],linewidth=3)

show()

(747,1000)的主点位置所生成的图像

在这里插入图片描述

(1000,1000)的主点位置所生成的图像

在这里插入图片描述

在第一幅图像上，底部的点在标记物上，就可以计算出变换到第二幅图像所对应的单应性矩阵

4.4 增强现实

首先需要下载pygame和pyopengl，在对应的虚拟环境中下载，通常情况下，我们会按照如下指令进行下载

pip install PyOpenGL PyOpenGL_accelerate
pip install pygame

在这里插入图片描述

4.4.1 PyGame和PyOpenGL

下载完成后，这里导入不会出现问题，会显示一些文字

from OpenGL.GL import *
from OpenGL.GLU import *
from OpenGL.GLUT import *
import pygame,pygame.image
from pygame.locals import *

在这里插入图片描述

4.4.2 从照相机矩阵到OpenGL格式

写入以下函数

import numpy as np
def set_projection_from_camera(K):
    glMatrixMode(GL_PROJECTION)
    glLoadIdentity()
    fx=K[0,0]
    fy=K[1,1]
    fovy=2*np.arctan(0.5*height/fy)*180/np.pi
    aspect=(width*fy)/(height*fx)
    near=0.1
    far=100.0
    gluPerspective(fovy,aspect,near,far)
    glViewport(0,0,width,height)

def set_modelview_from_camera(Rt):
    """从照相机姿态中获得模拟视图矩阵"""

    glMatrixMode(GL_MODELVIEW)
    glLoadIdentity()
    # 围绕x轴将茶壶旋转90度，使z轴向上
    Rx = np.array([[1, 0, 0], [0, 0, -1], [0, 1, 0]])
    # 获得旋转的最佳逼近
    R = Rt[:, :3]
    U, S, V = np.linalg.svd(R)
    R = np.dot(U, V)
    R[0, :] = -R[0, :]  # 改变x轴的符号
    # 获得平移量
    t = Rt[:, 3]
    # 获得4*4的的模拟视图矩阵
    M = np.eye(4)
    M[:3, :3] = np.dot(R, Rx)
    M[:3, 3] = t
    # 转置并压平以获取列序数值
    M = M.T
    m = M.flatten()
    # 将模拟视图矩阵替换成新的矩阵
    glLoadMatrixf(m)

4.4.3 在图像中放置虚拟物体

写入以下函数

def draw_background(imname):
    # 载入背景图像
    bg_image = pygame.image.load(imname).convert()
    bg_data = pygame.image.tostring(bg_image, "RGBX", 1)  # 将图像转为字符串描述
    
    glMatrixMode(GL_MODELVIEW)  # 将当前矩阵指定为投影矩阵
    glLoadIdentity()  # 把矩阵设为单位矩阵
    glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT)  # 清楚颜色、深度缓冲
    
    glEnable(GL_TEXTURE_2D)  # 纹理映射
    glBindTexture(GL_TEXTURE_2D, glGenTextures(1))
    glTexImage2D(GL_TEXTURE_2D, 0, GL_RGBA, width, height, 0, GL_RGBA, GL_UNSIGNED_BYTE, bg_data)
    glTexParameterf(GL_TEXTURE_2D, GL_TEXTURE_MAG_FILTER, GL_NEAREST)
    glTexParameterf(GL_TEXTURE_2D, GL_TEXTURE_MIN_FILTER, GL_NEAREST)
    
    # 绑定纹理
    glBegin(GL_QUADS)
    glTexCoord2f(0.0, 0.0);
    glVertex3f(-1.0, -1.0, -1.0)
    glTexCoord2f(1.0, 0.0);
    glVertex3f(1.0, -1.0, -1.0)
    glTexCoord2f(1.0, 1.0);
    glVertex3f(1.0, 1.0, -1.0)
    glTexCoord2f(0.0, 1.0);
    glVertex3f(-1.0, 1.0, -1.0)
    glEnd()
    
    glDeleteTextures(1)  # 清除纹理

def draw_teapot(size):  # 红色茶壶
    glEnable(GL_LIGHTING)
    glEnable(GL_LIGHT0)
    glEnable(GL_DEPTH_TEST)
    glClear(GL_DEPTH_BUFFER_BIT)
    # 绘制红色茶壶
    glMaterialfv(GL_FRONT, GL_AMBIENT, [0, 0, 0, 0])
    glMaterialfv(GL_FRONT, GL_DIFFUSE, [0.5, 0.0, 0.0, 0.0])
    glMaterialfv(GL_FRONT, GL_SPECULAR, [0.7, 0.6, 0.6, 0.0])
    glMaterialf(GL_FRONT, GL_SHININESS, 0.25 * 128.0)
    glutSolidTeapot(size)  # from OpenGL.GLUT import *

4.4.4 综合集成

import pickle

对主函数的两处进行修改
1. 添加glutInit()，因为需要初始化glut库，不然会报错
2. 因为是静态图片，渲染一次就行，把pygame.display.flip()提前

width, height = 1000, 747


def setup():  # 设置窗口和pygame环境
    pygame.init()
    pygame.display.set_mode((width, height), OPENGL | DOUBLEBUF)
    pygame.display.set_caption("OpenGL AR demo")

    
with open('ar_camera.pkl','rb') as f:
    K=pickle.load(f)
    Rt=pickle.load(f)
setup()

glutInit() # 初始化glut库

draw_background("book_perspective.bmp")
set_projection_from_camera(K)
set_modelview_from_camera(Rt)
draw_teapot(0.1)  # 显示红色茶壶


pygame.display.flip()
while True:
    event=pygame.event.poll()
    if event.type in (QUIT,KEYDOWN):
        break
pygame.quit()
sys.exit()

但是当运行主函数的时候，就会报如下的错误，网上说是使用pip下载的不全面，少了dll文件，所以得用whl文件下载，然后都在说从这个网站（https://www.lfd.uci.edu/~gohlke/pythonlibs/#pyopengl ）下载，发现这个网站已经把文件转移了，或者说不是这个链接了。

在这里插入图片描述

然后偶然在github上找到了这两个对应的文件OpenGL-Python/PyOpenGL_accelerate-3.1.6-cp38-cp38-win_amd64.whl at main · 11x1/OpenGL-Python · GitHub，这里需要注意的是，因为我的python是3.8版本，文件中cp38就是python3.8版本的意思，3.8版本应该是要下载PyOpenGL的3.1.6的版本

在这里插入图片描述

下载完成后，卸载掉原本的PyOpenGL和PyOpenGL_accelerate

pip uninstall pyopengl-accelerate

pip uninstall PyOpenGL

执行whl文件

pip install D:\Download\PyOpenGL-3.1.6-cp38-cp38-win_amd64.whl

pip install D:\Download\PyOpenGL_accelerate-3.1.6-cp38-cp38-win_amd64.whl

利用测试用例看看能不能用

import OpenGL
from OpenGL.GL import *
from OpenGL.GLU import *
from OpenGL.GLUT import *
def drawFunc():
    glClear(GL_COLOR_BUFFER_BIT|GL_DEPTH_BUFFER_BIT)
    glRotate(0.1, 5, 5, 0)

    glutWireTeapot(0.5)
    glFlush()


if __name__ == "__main__":
    glutInit()
    glutInitDisplayMode(GLUT_SINGLE|GLUT_RGBA)
    glutInitWindowPosition(0, 0)
    glutInitWindowSize(400, 400)
    glutCreateWindow("opengl")
    glutDisplayFunc(drawFunc)
    glutIdleFunc(drawFunc)
    glutMainLoop()