神仙公司(南京)
继续,神仙公司系列。
上一期我们介绍了 深圳的神仙公司,结果留言区的重点全都指向了 HW 和 BYD 🤣🤣
不愧是你们,但我们不是"那个"排行。
言归正传,这期给大伙安排呼声同样很高的城市:南京。
南京,是极少数古典韵味和现代脉动相结合的城市,也是毕业生就业定居中的热门城市。
在近两年的就业蓝皮书中「外省籍毕业生占比较高城市」、「就业薪资较高的城市」和「就业满意度较高的城市」的 TOP 10 榜单中均有上榜:
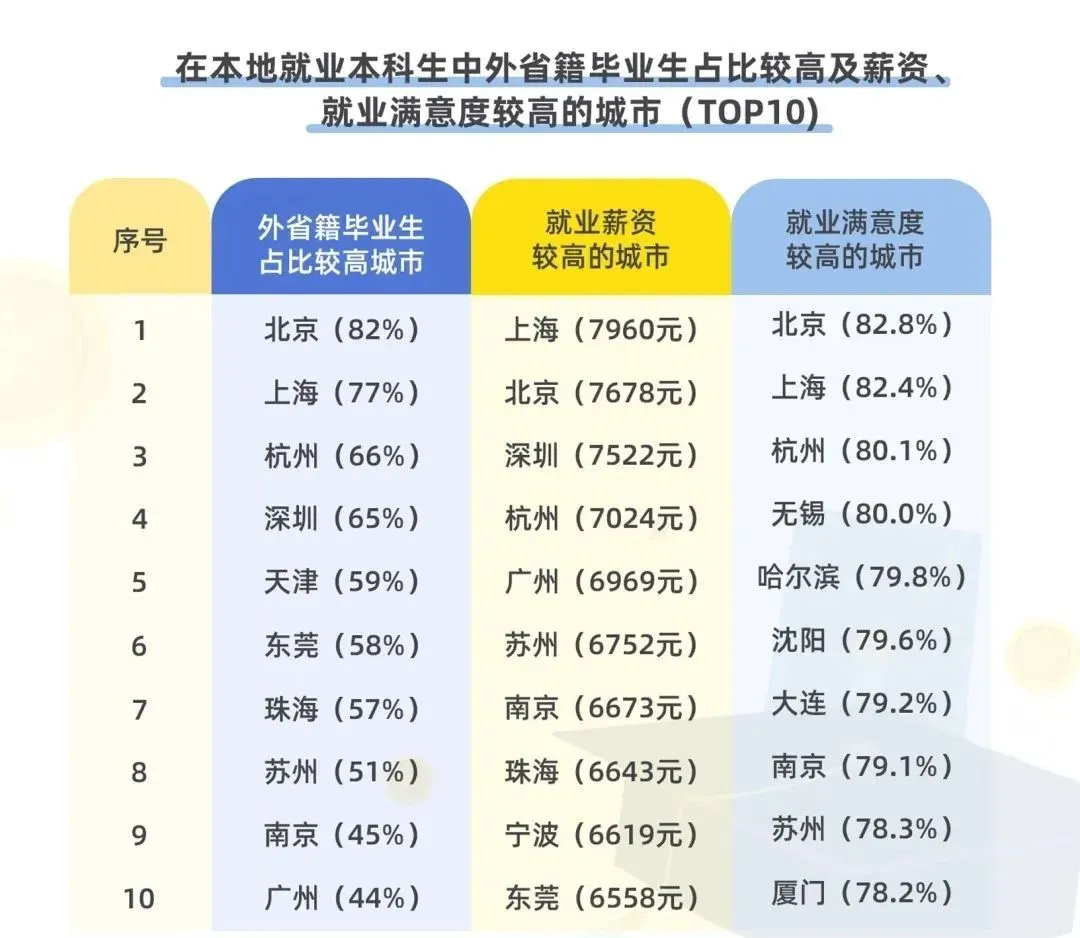
以下是坐标南京的神仙公司名单:
-
A.O.史密斯:制造业类外企,七险一金,弹性工作,通勤时间 8:00~16:30,班车覆盖全南京,饭堂中晚餐,薪资水平在南京属于中等偏上,14 薪; -
智网科技:中国联通集团投资子公司,国企性质,团队奖金,绩效提成,人才补贴,目前软硬件工程师都有在招,薪资水平 20k~45k,14薪; -
凯易迅:IT 类外企,不加班,不打卡,15~20 天年假,10 天带薪病假,六险一金,额外为员工提供人寿和意外保险,额外为员工子女提供医疗保险和托费报销,每年一次员工以及家属提供免费体检,在招工程师薪资范围在 25k~45k 之间,13 薪起,有实习机会(200~280 元/天); -
焦点科技:电子商务类的上市公司,六险一金,额外补充商业意外险,包三餐,免费下午茶,提供节日、婚育、季度、年度、业绩激励等各项基金,毕业生身份入职还有租房补贴,全员定期体检,股票激励计划; -
思杰:IT 类外企,不加班,不打卡,可居家办公,15~20 天年假,五险一金,额外补充商业保险,每年员工体检,员工扶持计划,下午茶及免费饮料水果,生日礼物,每年最高 7500 美元的教育资助,男员工有 18 周的陪产假; -
舍费勒:自动驾驶汽车领域,反内卷,955 工作制,准点下班,可居家办公,超长年假,补充医疗保险,员工储蓄计划(舍弗勒单方面向员工的个人账号存钱); -
贝湾科技:小而美互联网,旗下产品「扇贝单词」是 App Store 教育类别下的长期 TOP 10,公司主张不加班文化,工作氛围好,年假,节日福利,每天下午茶,每月生日会,每季度团建,在招岗位主要是客户端工程师,薪资范围 10k~20k;
关于「南京」以及「南京神仙公司」,你有什么想分享的呢,欢迎评论区留言。
...
回归主线。
周末,继续开心小算法。
题目描述
平台:LeetCode
题号:561
给定长度为
的整数数组 nums ,你的任务是将这些数分成 n 对, 例如
,使得从 1 到 n 的
总和最大。
返回该最大总和。
示例 1:
输入:nums = [1,4,3,2]
输出:4
解释:所有可能的分法(忽略元素顺序)为:
1. (1, 4), (2, 3) -> min(1, 4) + min(2, 3) = 1 + 2 = 3
2. (1, 3), (2, 4) -> min(1, 3) + min(2, 4) = 1 + 2 = 3
3. (1, 2), (3, 4) -> min(1, 2) + min(3, 4) = 1 + 3 = 4
所以最大总和为 4
示例 2:
输入:nums = [6,2,6,5,1,2]
输出:9
解释:最优的分法为 (2, 1), (2, 5), (6, 6). min(2, 1) + min(2, 5) + min(6, 6) = 1 + 2 + 6 = 9
提示:
贪心
我们先对数组进行排序。
由于每两个数,我们只能选择当前小的一个进行累加。
因此我们猜想应该从第一个位置进行选择,然后隔一步选择下一个数。这样形成的序列的求和值最大。
Java 代码:
class Solution {
public int arrayPairSum(int[] nums) {
int n = nums.length, ans = 0;
Arrays.sort(nums);
for (int i = 0; i < n; i += 2) ans += nums[i];
return ans;
}
}
C++ 代码:
class Solution {
public:
int arrayPairSum(vector<int>& nums) {
int n = nums.size(), ans = 0;
sort(nums.begin(), nums.end());
for (int i = 0; i < n; i += 2) ans += nums[i];
return ans;
}
};
Python 代码:
class Solution:
def arrayPairSum(self, nums: List[int]) -> int:
nums.sort()
ans = 0
for i in range(0, len(nums), 2):
ans += nums[i]
return ans
TypeScript 代码:
function arrayPairSum(nums: number[]): number {
let n = nums.length, ans = 0;
nums.sort((a, b) => a - b);
for (let i = 0; i < nums.length; i += 2) ans += nums[i];
return ans;
};
-
时间复杂度: -
空间复杂度:
证明
解法不难,重点是要证明该做法的正确性,这才是"贪心"类算法题的意义。
我们用反证法来证明下,为什么这样选择的序列的求和值一定是最大的:
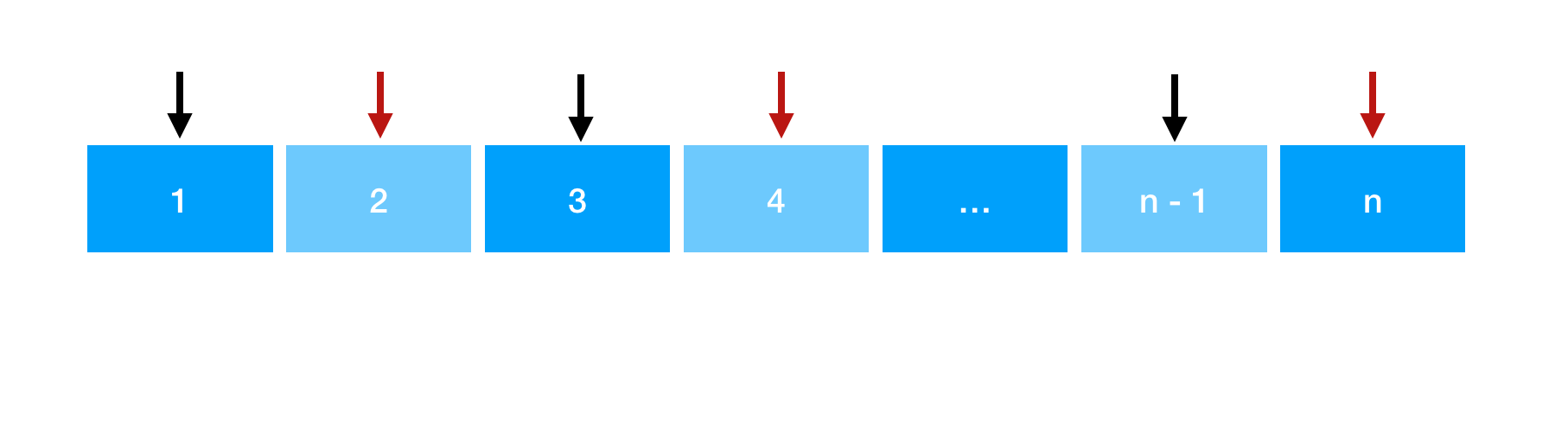
猜想:对数组进行排序,从第一个位置进行选择,然后隔一步选择下一个数。这样形成的序列的求和值最大(下图黑标,代表当前被选择的数字)。

之所以我们能这么选择,是因为每一个被选择的数的「下一位位置」都对应着一个「大于等于」当前数的值(假设位置为 k),使得当前数在 min(a,b) 关系中能被选择(下图红标,代表保证前面一个黑标能够被选择的辅助数)。
假如我们这样选择的序列求和不是最大值,那么说明至少我们有一个值选错了,应该选择更大的数才对。
那么意味着我们「某一位置」的黑标应该从当前位置指向更后的位置。
「PS. 因为要满足 min(a, b) 的数才会被累加,因此每一个红标右移(变大)必然导致原本所对应的黑标发生「同样程度 或 不同程度」的右移(变大)」
这会导致我们所有的红标黑标同时往后平移。
最终会导致我们最后一个黑标出现在最后一位,这时候最后一位黑标不得不与我们第 k 个位置的数形成一对。
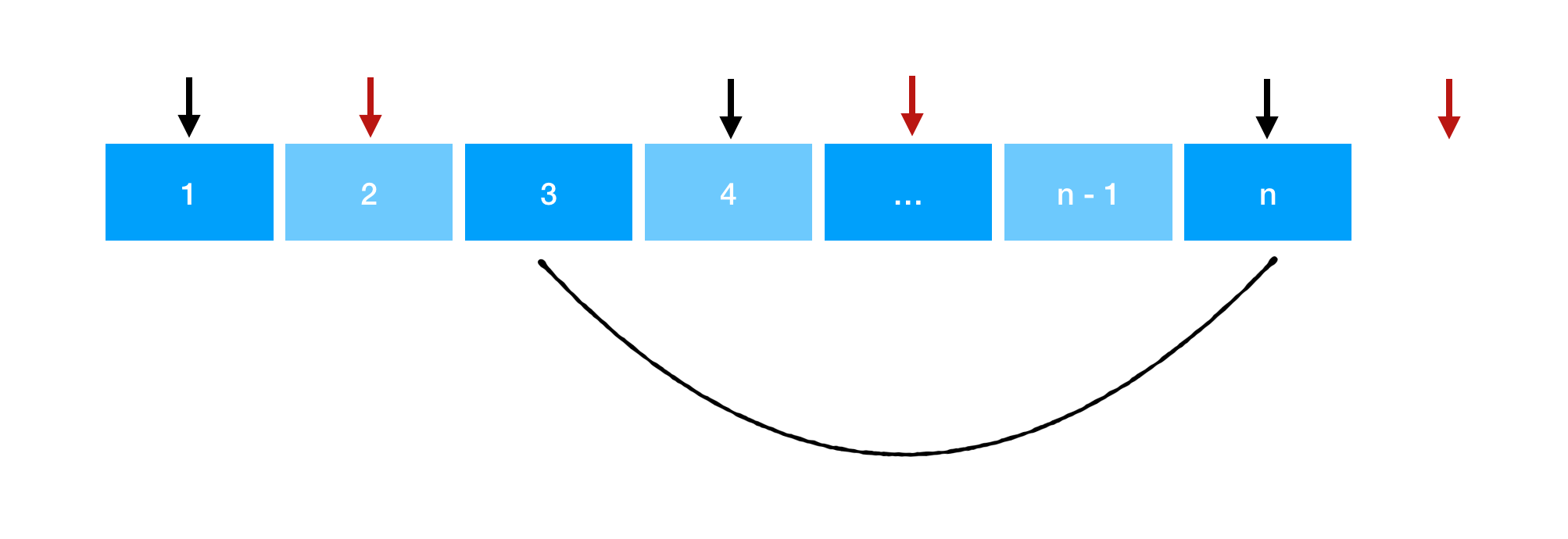
我们看看这是求和序列的变化(k 位置前的求和项没有发生变化,我们从 k 位置开始分析):
-
原答案 = nums[k] + nums[k + 2] + ... + nums[n - 1] -
调整后答案 = nums[k + 1] + nums[k + 3] + ... + nums[n - 2] + min(nums[n], nums[k])由于min(nums[n], nums[k])中必然是nums[k]被选择。因此: 调整后答案 =nums[k] + nums[k + 1] + nums[k + 3] + ... + nums[n - 2]
显然从原答案的每一项都「大于等于」调整后答案的每一项,因此「不可能在「假想序列」中通过选择别的更大的数得到更优解,假想得证。」
最后
巨划算的 LeetCode 会员优惠通道目前仍可用 ~
使用福利优惠通道 leetcode.cn/premium/?promoChannel=acoier,年度会员 有效期额外增加两个月,季度会员 有效期额外增加两周,更有超大额专属 🧧 和实物 🎁 福利每月发放。
我是宫水三叶,每天都会分享算法知识,并和大家聊聊近期的所见所闻。
欢迎关注,明天见。
更多更全更热门的「笔试/面试」相关资料可访问排版精美的 合集新基地 🎉🎉