5.理想热力循环

5.1 卡诺定理

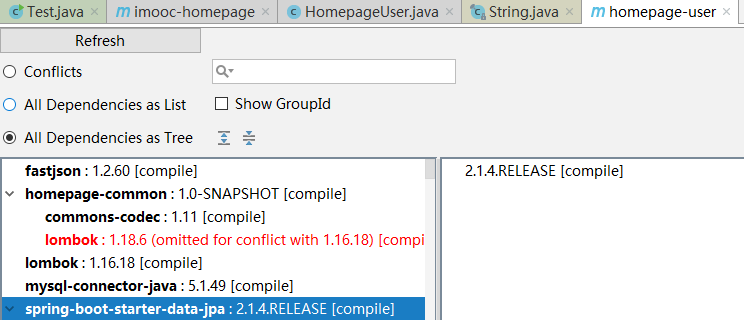
考虑这样的一个实际的热力循环，其过程为存在一个高温热源，工作介质从该高温热源中吸取热量Q1，其中一部分通过工作介质对外做功转化为机械功，剩余一部分热量排给低温热源。

根据热力学第一定律
$$W_0=Q_1-Q_2\text{\hspace{1em}(5.1)}$$
该热力循环的热效率为
$${\eta }_t=\frac{收获}{消耗}=\frac{W_0}{Q_1}=\frac{Q_1-Q_2}{Q_1}=1-\frac{Q_2}{Q_1}\text{\hspace{1em}(5.2)}$$
将高温热源、低温热源和工作介质一起当成一个热力学孤立系统，那么整个孤立系统的熵
$$\begin{gathered} \Delta S_{孤立系}=\Delta S_{高温热源}+\Delta S_{低温热源}+\Delta S_{工作介质} \\ =\frac{-Q_1}{T_1}+\frac{Q_2}{T_2}+0 \\ =\frac{Q_2}{T_2}-\frac{Q_1}{T_1}\ge 0\text{\hspace{1em}(5.3)} \end{gathered}$$
因此，有
$$\frac{Q_2}{Q_1}\ge \frac{T_2}{T_1}\text{\hspace{1em}(5.4)}$$
代入前式，该循环的热效率
$${\eta }_t=1-\frac{Q_2}{Q_1}\le 1-\frac{T_2}{T_1}\text{\hspace{1em}(5.5)}$$

5.2 卡诺循环

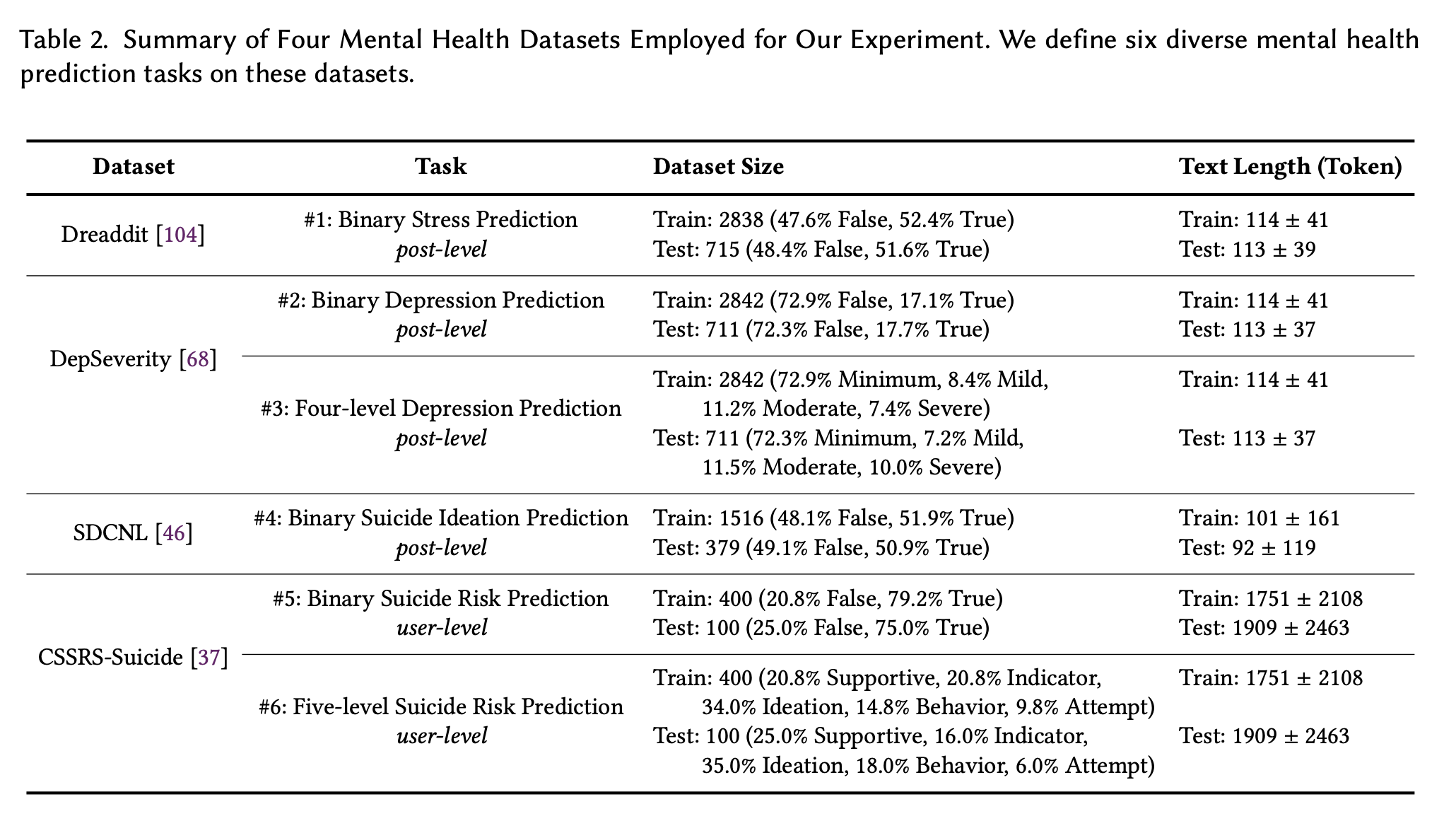
考虑这样一个热力循环，他从高温热源无传热温差的吸热，并且之后进行无摩擦的等熵膨胀，在向低温热源释放热量时也是无温差的，并且之后经历等熵压缩回到初始状态，详见下图，在经历这样的循环后其热效率为
$$\begin{gathered} {\eta }_{t,C}=\frac{W_{0C}}{Q_{1C}}=\frac{Q_{1C}-Q_{2C}}{Q_{1C}}=1-\frac{Q_{2C}}{Q_{1C}} \\ 1-\frac{T_2(S_b-S_c)}{T_1(S_a-S_d)}=1-\frac{T_2}{T_1}\text{\hspace{1em}(5.6)} \end{gathered}$$

因此，热力循环最高的热效率为$1-\frac{T_2}{T_1}$，提高热效率的途径主要根据需要提高吸热温度或者降低放热温度。

5.3 逆向卡诺循环

如果热力循环的方向是5.2循环的逆序方向，那么称之为逆向卡诺循环，如下图所示，实际的理想制冷循环就是这样的循环。
制冷循环的热经济性用制冷系数衡量，制冷系数就是制冷循环中从冷库吸取的热量比上循环净功，如下式所示。

$$\begin{gathered} {\epsilon }_C=\frac{收获}{消耗}=\frac{q_2}{w_0}=\frac{T_0\Delta s}{(T_H-T_0)\Delta s}=\frac{T_0}{T_H-T_0} \\ =\frac{1}{\frac{T_H}{T_0}-1}\text{\hspace{1em}(5.6)} \end{gathered}$$
其中在制冷循环中一般$T_H$为大气温度，$T_0$为冷库或者冷房间的温度。
从上式可得，当大气温度是冷室温度的两倍以上时，制冷系数小于1，当大气温度是冷室温度的两倍以内时，制冷系数大于1。