codeforces Round 970 (Div. 3)(A-F)

文章目录

- [Codeforces Round 970 (Div. 3)](https://codeforces.com/contest/2008)
- - - A-[Sakurako's Exam](https://codeforces.com/contest/2008/problem/A)
    - B-[Square or Not](https://codeforces.com/contest/2008/problem/B)
    - C-[Longest Good Array](https://codeforces.com/contest/2008/problem/C)
    - D-[Sakurako's Hobby](https://codeforces.com/contest/2008/problem/D)
    - E-[Alternating String](https://codeforces.com/contest/2008/problem/E)
    - F-[Sakurako's Box](https://codeforces.com/contest/2008/problem/F)

Codeforces Round 970 (Div. 3)

A-Sakurako’s Exam

#include<bits/stdc++.h>

using namespace std;

signed main()
{
  int t;
  cin>>t;
  while(t--)
  {
    int a,b;
    cin>>a>>b;
    if(a%2==0&&b%2==0) 
    {
        puts("YES");
        continue;
    }
    b+=(a/2);
    a%=2;
    if(a%2==0&&b%2==0) puts("YES");
    else puts("NO");
  }
  return 0;
}

谁不够给谁属于是

不懂了，为什么考虑奇偶还是不行

woc等一个ac有多难

泪目了

就是先判断b是否为零的情况

#include<bits/stdc++.h>

using namespace std;

signed main()
{
  int t;
  cin>>t;
  while(t--)
  {
    int a,b;
    cin>>a>>b;
    if(!b)
    {
      if(a%2==0)
      {
        puts("YES");
        continue;
      }
      else
      {
        puts("NO");
        continue;
      }
    }
    
    if(b%2)
    {
      if(a>=2)
      {
          a-=2;
          b+=1;
      }
      
      if(b%2==0&&a%2==0)
      {
        puts("YES");
        continue;
      }
    }
    else
    {
      if(a%2==0)
      {
        puts("YES");
        continue;
      }
    }
    puts("NO");
  }
  return 0;
}

B-Square or Not

要求是正方形，且符合另面都是零，外面都是1包围的01串

是否是一个平方数

感觉我这样循环会被卡死

居然过了，也是神奇，不卡我

#include<bits/stdc++.h>

using namespace std;
map<int,int> mp;
const int N=1e3+10;

void pre()
{
  for(int i=1;i<=2e5;i++)
  {
    mp[i*i]=i;
  }
}

signed main()
{
  int t;
  cin>>t;
  pre();
  while(t--)
  {
    int n;
    cin>>n;
    string s;
    cin>>s;
    
    if(!mp[n])
    {
      puts("No");
    }
    else
    {
      int x=mp[n];
      int g[N][N];
      int flag=1;
      for(int i=1;i<x-1;i++)
      {
        for(int j=1;j<x-1;j++)
        {
          //cout<<s[i*x+j]<<' ';
          if(s[i*x+j]=='1')
          {
            
            flag=0;
            break;
          }
        }
        //cout<<endl;
        if(!flag) break;
      }
      if(!flag) 
      {
          puts("NO");
          continue;
      }
      puts("YES");
    }
    
  }
  return 0;
}

C-Longest Good Array

直接暴力会怎样，感觉不会爆，开到两秒了都

意思是求长度，所以一定从最低开始枚举

1,2,3,4。。。。这样的枚举

也是好出思路，一下就打出来了

#include<bits/stdc++.h>

using namespace std;

signed main()
{
  int t;
  cin>>t;
  while(t--)
  {
    int l,r;
    cin>>l>>r;
    int delt=1;
    int res=1;
    for(int i=l+delt;i<=r;i+=delt)
    {
 	  delt++;    
      res++;
      //cout<<i<<' ';
    }
    //cout<<endl;
    //if(r-l+1==2) res+=1;
    cout<<res<<endl;
  }
  return 0;
}

D-Sakurako’s Hobby

有函数f可以构造可达

可达有什么用，需要可达到哪里去

其实没读懂题目，赛时也没花时间做

我要泪目了，看到dsu这个标签，去查了一下，发现是并查集，然后联想了一下发现真的有点子并查集在的

其实题目这里也是有在提醒的，其实我倒是没有看出来dp

#include<bits/stdc++.h>

using namespace std;
const int N=2e5+10;
int a[N],pa[N];

int find(int x)
{
  if(x!=pa[x]) pa[x]=find(pa[x]);
  return pa[x];
}

signed main()
{
  int t;
  cin>>t;
  while(t--)
  {
    int n;
    cin>>n;
		for(int i=1;i<=n;i++) pa[i]=i;
    for(int i=1;i<=n;i++) cin>>a[i];
    char s[N];
    cin>>s+1;
    
    for(int i=1;i<=n;i++)
    {
      int x=i,y=a[i];
      x=find(i),y=find(y);
      if(x!=y)
      {
        pa[x]=y;
      }
    }
    for(int i=1;i<=n;i++)
    {
      cout<<s[pa[i]]<<' ';
    }
    cout<<endl;
  }
  return 0;
}

别把要输出的F和题目给的p函数搞混了

感觉这两个函数是互逆的

感觉读不太懂这个题

懂了，F(i) 是从i出发能经过多少的黑色，也就是0

可不可以用带权并查集

#include<bits/stdc++.h>

using namespace std;
const int N=2e5+10;
int a[N],pa[N],cnt[N];

int finda(int x)
{
  if(x!=pa[x])
  {
    
    pa[x]=find(pa[x]);
    cnt[x]+=pa[x];
    
  }
  return pa[x];
}

signed main()
{
  int t;
  cin>>t;
  while(t--)
  {
    int n;
    cin>>n;
    memset(cnt,0,sizeof cnt);
		for(int i=1;i<=n;i++) pa[i]=i;
    for(int i=1;i<=n;i++) cin>>a[i];
    char s[N];
    cin>>s+1;
    for(int i=1;i<=n;i++) 
    {
        if(s[i]=='0') 
        {
            cnt[i]++;
        }
        //cout<<cnt[i]<<' ';
    }
    //cout<<endl;
    
    for(int i=1;i<=n;i++)
    {
      int x=i,y=a[i];
      x=find(i),y=find(y);
      if(x!=y)
      {
        pa[x]=y;
      }
    }
    
    for(int i=1;i<=n;i++) cout<<cnt[i]<<' ';
    cout<<endl;
    
    /*for(int i=1;i<=n;i++)
    {
      cout<<cnt[pa[i]]<<' ';
    }
    cout<<endl;*/
    
  }
  return 0;
}

不知道怎么处理如何跳，学完下面两个ac代码会了

是不可能出现红框这种情况的

题目开头有说明

也就是说一定会有连通块是强连通的

#include<bits/stdc++.h>

using namespace std;
const int N=2e5+10;
int a[N],pa[N],cnt[N];

int find(int x)
{
  if(x!=pa[x])
  {
    pa[x]=find(pa[x]); 
  }
  return pa[x];
}

signed main()
{
  int t;
  cin>>t;
  while(t--)
  {
    int n;
    cin>>n;
    memset(cnt,0,sizeof cnt);
	for(int i=1;i<=n;i++) pa[i]=i;
    for(int i=1;i<=n;i++) cin>>a[i];
    char s[N];
    cin>>s+1;
    
    for(int i=1;i<=n;i++)
    {
      int x=i,y=a[i];
      x=find(i),y=find(y);
      if(x!=y)
      {
        pa[x]=y;
      }
    }
    
    for(int i=1;i<=n;i++) 
    {
        if(s[i]=='0') 
        {
          	//最终跳到父节点，代表我从在这个过程中一共能走过多少黑点
            cnt[pa[i]]++;
        }
    }
    
    for(int i=1;i<=n;i++) cout<<cnt[pa[i]]<<endl;
  }
  return 0;
}

这个是带着模拟的意味做的，有掺杂自己思考的ac代码

但是while不等于那里真的不会死循环吗，不会的，因为用的是并查集，如果到最后父节点是自己就一定会跳出循环，但其实它这个相当于多开了一个ans 数组去记录每一个节点的在从第一个点开始跳的时候会积累多少的黑点，一个连通块的会在遍历到第一个连通块里的点的时候就确定连通块里各个点的ans。

#include<bits/stdc++.h>
using namespace std;
int p[200001],ans[200001],root;
string s;
int solve(int i){
	if(ans[i]!=-1)return ans[i];
	int x=0,a=i;
	do{
		x+=s[a-1]=='0';
		a=p[a];
	}while(a!=i);
	do{
		ans[a]=x;
		a=p[a];
	}while(a!=i);
	return ans[i];
	
}
int main(){
	int t;cin>>t;
	while(t--){
		int n;cin>>n;
		for(int i=1;i<=n;++i)cin>>p[i];
		cin>>s;
		memset(ans,-1,sizeof ans);
		for(int i=1;i<=n;++i){root=i;cout<<solve(i)<<' ';}
		cout<<'\n';
	}
	return 0;
}

这个是真并查集

#include<bits/stdc++.h>
using namespace std;
int main()
{
	int t;
	scanf("%d",&t);
	while(t--)
	{
		int n;
		scanf("%d",&n);
		vector<int>p(n+1),fa(n+1),cnt(n+1);
		for(int i=1;i<=n;i++)fa[i]=i,scanf("%d",&p[i]);
		function<int(int)>find=[&](int i){return fa[i]==i?i:fa[i]=find(fa[i]);};
		for(int i=1;i<=n;i++)fa[find(i)]=find(p[i]);
		string s;
		cin>>s;
		for(int i=1;i<=n;i++)if(s[i-1]=='0')++cnt[find(i)];
		for(int i=1;i<=n;i++)printf("%d ",cnt[find(i)]);
		printf("\n");
	}
	return 0;
}

E-Alternating String

可替换字符的定义是，一个长度为偶数的字符串，且奇数位置的字符串的字符相同,偶数位置的字符相同

操作：

最多不超过一次的删除
选择字符串中的一个字符替换成任何一个字符

差点读不懂，就是说你作为一个朋友需要送给你的朋友一个可替换的字符串

需要在原串的基础上操作多少次

分别统计奇数位置上的字符和偶数位置上的字符有多少相同的，看哪个相同的字符更多

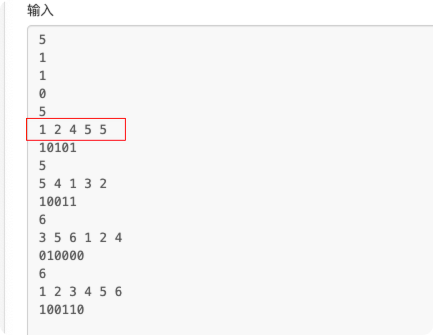
第一打想简单了，删除的位置是可以任意的，前台样例的第十个例子

所以应该怎么样去替换，怎么样去删除，删除哪一个位置最合适

#include<bits/stdc++.h>

using namespace std;
const int N=2e5+10;
int odd[26],even[26];

signed main()
{
  int t;
  cin>>t;
  while(t--)
  {
    int n;
    int ans=0;
    cin>>n;
    memset(odd,0,sizeof odd);
    memset(even,0,sizeof even);
    string s;
    cin>>s;
    
    if(n%2)
    {
      ans+=1;
      n-=1;
    }
    
    if(n==2)
    {
      puts("0");
      continue;
    }
    
    int oddmax=0;
    int evenmax=0;
    for(int i=0;i<s.size()-ans;i+=2)
    {
      odd[s[i]-'a']++;
      oddmax=max(oddmax,odd[s[i]-'a']);
    }
    
    for(int i=1;i<s.size()-ans;i+=2)
    {
      even[s[i]-'a']++;
      evenmax=max(evenmax,even[s[i]-'a']);
    }
    ans+=(n/2-oddmax);
    ans+=(n/2-evenmax);
    cout<<ans<<endl;
    
  }
  return 0;
}

学习借鉴了好友Dorothy__的代码

感觉Dorothy是一个调用api的高手

看他一篇题解每次都能学到新函数，太多函数啦，先不学这个代码了

#include<bits/stdc++.h>
using namespace std;
using ll=long long;
const int N=300005,P=998244353;
auto solve(){
    int n;
    string s;
    cin>>n>>s;
    s="  "+s;
    vector<array<int,26>> f(n+2);
    for(int i=2;i<=n+1;i++){
        f[i]=f[i-2];
        f[i][s[i]-'a']++;
    }
    auto check=[&](const array<int,26> &a){
        int mx=*max_element(begin(a),end(a));
        int sum=accumulate(begin(a),end(a),0);
        return sum-mx;
    };
    if(n%2==0){
        return check(f.back())+check(f[f.size()-2]);
    }
    auto dec=[&](auto &x,auto &y){
        for(int i=0;i<26;i++){
            x[i]-=y[i];
        }
    };
    auto add=[&](auto &x,auto &y){
        for(int i=0;i<26;i++){
            x[i]+=y[i];
        }
    };
    int ans=1e9;
    for(int i=2;i<=n+1;i++){
        array<int,26> b[2];
        if(i&1){
            b[0]=f[i-1];
            add(b[0],f[f.size()-2]);
            dec(b[0],f[i]);
            b[1]=f[i-2];
            add(b[1],f[f.size()-1]);
            dec(b[1],f[i-1]);
        }else{
            b[0]=f[i-2];
            add(b[0],f[f.size()-2]);
            dec(b[0],f[i-1]);
            b[1]=f[i-1];
            add(b[1],f[f.size()-1]);
            dec(b[1],f[i]);
        }
        // for(auto v:b){
        //     for(auto x:v)
        //         printf("%d ",x);
        //     puts("");
        // }
        // puts("");
        ans=min(ans,check(b[0])+check(b[1]));
    }
    return ans+1;
}
int main(){
    ios::sync_with_stdio(false);
    cin.tie(0);
    int t=1;
    cin>>t;
    while(t--){
        // solve();
        cout<<solve()<<'\n';
        // cout<<(solve()?"Yes":"No")<<'\n';
    }
    return 0;
}

一个用dp实现且我能够看懂思路复现的代码

之后的题目也可以在思想上和这个佬交流一下

代码实现很牛逼。

当字符串长度为n时，需要删除一个字符并看是否需要在剩下的字符中找到应该替换的字符

在奇数序列和偶数序列

删掉的那个字符会影响counts，但是用prev_count去恢复之前删掉的字符，如果之前删掉的位置时奇数的位置，那么最近的一次删除一定是偶数位的，因为我是这样奇偶奇偶地枚举i的，所以之前删除的奇数位字符c和现存的偶数位构成奇数位的序列。同理，之前删除的偶数位的字符c和现存的奇数位构成偶数位。

#include <iostream>
#include <iomanip>
#include <string>
#include <map>
#include <random>
#include <algorithm>
#include <set>
#include <deque>
#include <bitset>
#define MAXN 100000
#define ll long long
using namespace std;

ll A[MAXN+2];
int main() {
    int T;
    cin>>T;
    for(int t=1;t<=T;t++) {
        int n;
        cin>>n;
        string S;
        cin>>S;
        vector<vector<int>> counts(2, vector<int>(26,0));
        for(int i=0;i<n;i++) {
            counts[i%2][S[i]-'a']++;
        }
        int ans=1e9;
        if (n&1) {
            vector<vector<int>> prev_counts(2, vector<int>(26, 0));
            for(int i=0;i<n;i++) {
                counts[i%2][S[i]-'a']--;
                int maxe=0;
                int maxo=0;
                for(int c=0;c<26;c++) {
                    maxe=max(maxe,prev_counts[0][c]+counts[1][c]);
                    maxo=max(maxo,prev_counts[1][c]+counts[0][c]);
                }
                ans=min(ans,n-maxe-maxo);
                prev_counts[i%2][S[i]-'a']++;
            }
        } else {
            int maxe=0;
            int maxo=0;
            for(int c=0;c<26;c++) {
                maxe=max(maxe,counts[0][c]);
                maxo=max(maxo,counts[1][c]);
            }
            ans=min(ans,n-maxe-maxo);
        }
        cout << ans << endl;
    }
}

关于dp的复现

#include<bits/stdc++.h>

using namespace std;
const int N=1e5+10;

signed main()
{
  int t;
  cin>>t;
  while(t--)
  {
    int n;
    cin>>n;
    string s;
    cin>>s;
    vector<vector<int> > counts(2,vector<int>(26,0));
    for(int i=0;i<n;i++)
    {
      counts[i%2][s[i]-'a']++;
    }
    
    int maxe=0,maxo=0;
    vector<vector<int> > pre_counts(2,vector<int>(26,0));
    int ans=1e9;
    if(n&1)
    {
      for(int i=0;i<n;i++)
      {
        counts[i%2][s[i]-'a']--;
        for(int a=0;a<26;a++)
        {
          maxe=max(maxe,pre_counts[0][a]+counts[1][a]);
          maxo=max(maxo,pre_counts[1][a]+counts[0][a]);
        }
        ans=min(ans,n-maxe-maxo);
        pre_counts[i%2][s[i]-'a']++;
      }
    }
    else
    {
      for(int a=0;a<26;a++)
      {
        maxe=max(maxe,counts[1][a]);
        maxo=max(maxo,counts[0][a]);
      }
      ans=min(ans,n-maxe-maxo);
    }
    cout<<ans<<endl;
  }
  return 0;
}

F-Sakurako’s Box

给我的感觉像是组合计数加上费马小定理求逆元

$C_n^2$

#include<bits/stdc++.h>

using namespace std;
const int N=2e5+10;
typedef long long ll;
const ll mod=1e9+7;
ll a[N];
ll C[N];

void pre()
{
  for(int i=2;i<=N;i++)
  {
    C[i]=i*(i-1)/2%mod;
    //if(i<=20) cout<<i<<' '<<C[i]<<endl;
    
  }
}

ll qui(ll a,ll k)
{
  ll res=1;
  while(k)
  {
    if(k&1) res=res*a%mod;
    k>>=1;
    a=a*a%mod;
  }
  return res;
}

signed main()
{
  int t;
  scanf("%d",&t);
  pre();
  while(t--)
  {
    int n;
    scanf("%d",&n);
    ll res=0;
    for(int i=1;i<=n;i++)
    {
      scanf("%d",&a[i]);
    }
    
    for(int i=1;i<=n;i++)
    {
      for(int j=i+1;j<=n;j++)
      {
        res=(res+a[i]*a[j]%mod)%mod;
        //cout<<res<<' ';
      }
    }
    //cout<<endl;
    ll zu=C[n];
    //zu=qui(zu,mod-2);
    //cout<<qui(zu,mod-2)<<endl;
    //cout<<zu<<endl;
    cout<<(res*(qui(zu,mod-2)%mod))%mod<<endl;
    //cout<<res/zu<<endl;
  }
  return 0;
}

我真是草了

快速幂求逆元没有返回值一直在那算不明白，他妈的

虽然最原始的思路在第五个样例tle但是，最后十几分钟因为没有返回res在那死循环的找真是他妈蠢

tle了cin换成scanf也没有用，应该还是在计算res那里有点子可以优化的地方

看到一ac写的代码，sum那里不知道为什么

woc太聪明了，先加起来再乘

#include <bits/stdc++.h>
using namespace std;

const int MOD = 1e9 + 7;
typedef long long ll;

ll power(ll a, ll b, ll mod)
{
    ll res = 1;
    while (b)
    {
        if (b & 1)
            res = (res * a) % mod;
        a = (a * a) % mod;
        b >>= 1;
    }
    return res;
}

void solve()
{
    int n;
    cin >> n;
    vector<ll> a(n);
    ll sum = 0;
    for (int i = 0; i < n; i++)
    {
        cin >> a[i];
        sum = (sum + a[i]) % MOD;
    }
    if (n == 2)
    {
        cout << (a[0] * a[1]) % MOD << "\n";
        return;
    }
    ll ans = 0;
    for (int i = 0; i < n; i++)
    {
        sum = (sum - a[i] + MOD) % MOD;
        ans = (ans + ((sum * a[i]) % MOD)) % MOD;
    }
    if (n > 1)
    {
        ll totalPairs = ((ll)n * (n - 1) / 2) % MOD;
        ll inv = power(totalPairs, MOD - 2, MOD);
        ans = (ans * inv) % MOD;
    }
    else
    {
        ans = 0;
    }
    cout << ans << "\n";
}

int main()
{
    ios::sync_with_stdio(0);
    cin.tie(0);
    int t;
    cin >> t;
    while (t--)
    {
        solve();
    }
    return 0;
}

组合计数里面没有勤取模导致出错

#include<bits/stdc++.h>

using namespace std;
const int N=2e5+10;
typedef long long ll;
const ll mod=1e9+7;
ll a[N];
ll C[N];

void pre()
{
  for(int i=2;i<=N;i++)
  {
    C[i]=(ll)i*(i-1)/2%mod;
  }
}

ll qui(ll a,ll k)
{
  ll res=1;
  while(k)
  {
    if(k&1) res=res*a%mod;
    k>>=1;
    a=a*a%mod;
  }
  return res;
}

signed main()
{
  int t;
  scanf("%d",&t);
  pre();
  while(t--)
  {
    int n;
    scanf("%lld",&n);
    ll sum=0;
  
    for(int i=1;i<=n;i++)
    {
      scanf("%lld",&a[i]);
      sum=(sum+a[i])%mod;
    }
    if(n==2)
    {
        cout<<(a[1]*a[2])%mod<<endl;
        continue;
    }
    ll res=0;
    if(n>1)
    {
        
        for(int i=1;i<=n;i++)
        {
          sum=(sum-a[i]+mod)%mod;
          res=(res+sum*a[i]%mod)%mod;
        }
        ll zu=C[n];
        res=(res*(qui(zu,mod-2)%mod))%mod;
    }
    else res=0;
    

    cout<<res<<endl;
  }
  return 0;
}