题目链接: https://leetcode.cn/problems/decode-ways/
视频题解: https://www.bilibili.com/video/BV181YKeGE3E/
LeetCode 91. 解码方法
题目描述
一条包含字母 A-Z 的消息通过以下映射进行了 编码 :
'A' -> "1"
'B' -> "2"
...
'Z' -> "26"
要 解码 已编码的消息,所有数字必须基于上述映射的方法,反向映射回字母(可能有多种方法)。例如,"11106" 可以映射为:
"AAJF",将消息分组为(1 1 10 6)"KJF",将消息分组为(11 10 6)
注意,消息不能分组为 (1 11 06) ,因为 "06" 不能映射为 "F" ,这是由于 "6" 和 "06" 在映射中并不等价。
给你一个只含数字的 非空 字符串 s ,请计算并返回 解码 方法的 总数 。
题目数据保证答案肯定是一个 32 位 的整数。
举个例子:
输入: s = "12"
输出: 2
解释: 它可以解码为 "AB"(1 2)或者 "L"(12)。
视频题解
解码方法
思路来源
思路来源
知识回顾
动态规划是一种通过将原问题分解为子问题来求解复杂问题的算法思想。它通常用于求解最优化问题,例如最长公共子序列、背包问题等。动态规划的核心思想是将原问题分解为若干个子问题,通过求解子问题的最优解推导出原问题的最优解。可以通过两点来判断一个问题能不能通过动态规划来解,一是该问题是否存在递归结构,二是对应的子问题能否记忆化。动态规划可以通过带备忘录的自上而下的递归和自下而上的迭代来分别实现。由于递归需要用到栈来实现,一些语言对递归的深度是有限制的,所以自下而上的迭代是动态规划的最佳实现方式。
思路解析
计算s的[i,n)区间解码数量时,可以把问题拆解成独立的子问题:
- 如果
s[i]在'1'~'9'范围内,可以被单独解码,这个时候被解码的数量其实就是子问题[i+1,n)区间解码数量。 - 如果
s[i]s[i+1]在"10"~"26"范围内,可以被组合解码,这个时候被解码的数量其实就是子问题[i+2,n)区间解码数量。 - 如果
1和2中的条件都满足,那么被解码的数量就是子问题[i+1,n)区间和子问题[i+2,n)区间解码数量之和。
上述过程的子问题是可以记忆化的,我们增加一个备忘录来保存子问题的解,推导原问题时避免重复计算。这就满足了使用动态规划的条件:存在递归结构和子问题可以记忆化。所以本题可以用动态规划来解。动态规划可以通过带备忘录的自上而下的递归和自下而上的迭代来分别实现。
方法1 自上而下的递归+备忘录
递归的关键在于划分子问题和确定跳出递归的条件。
递归是一种自上而下的推导方式,这里跳出递归条件就是子问题区间为空或备忘录中已经保存了子问题的解。
C++代码
class Solution {
public:
int numDecodings(string s) {
map<int, int> count;
count[s.length()] = 1;
return dfs(s, count, 0);
}
int dfs(string& s, map<int, int>& count, int i) {
//跳出递归条件
if (count.find(i) != count.end()) {
return count[i];
}
//跳出递归条件
if (s[i] == '0') {
return 0;
}
//子问题处理
int res = dfs(s, count, i + 1);
if (i + 1 < s.length() && (s[i] == '1' || (s[i] == '2'&& s[i + 1] >= '0' && s[i + 1] <= '6'))) {
//子问题处理
res += dfs(s, count, i + 2);
}
//更新备忘录
count[i] = res;
return res;
}
};
java代码
class Solution {
public int numDecodings(String s) {
Map<Integer, Integer> count = new HashMap<>();
count.put(s.length(), 1);
return dfs(s, count, 0);
}
public int dfs(String s, Map<Integer, Integer> count, int i) {
// 跳出递归条件
if (count.containsKey(i)) {
return count.get(i);
}
// 跳出递归条件
if (s.charAt(i) == '0') {
return 0;
}
// 子问题处理
int res = dfs(s, count, i + 1);
if (i + 1 < s.length() && (s.charAt(i) == '1' || (s.charAt(i) == '2' && s.charAt(i + 1) >= '0' && s.charAt(i + 1) <= '6'))) {
// 子问题处理
res += dfs(s, count, i + 2);
}
// 更新备忘录
count.put(i, res);
return res;
}
}
python代码
class Solution:
def numDecodings(self, s: str) -> int:
count = {len(s): 1}
return self.dfs(s, count, 0)
def dfs(self, s, count, i):
# 跳出递归条件
if i in count:
return count[i]
# 跳出递归条件
if s[i] == '0':
return 0
# 子问题处理
res = self.dfs(s, count, i + 1)
if i + 1 < len(s) and (s[i] == '1' or (s[i] == '2' and s[i + 1] >= '0' and s[i + 1] <= '6')):
# 子问题处理
res += self.dfs(s, count, i + 2)
# 更新备忘录
count[i] = res
return res
复杂度分析
时间复杂度: O(n),n为s的长度。
空间复杂度: O(n),n为s的长度。
方法2 自下而上的迭代
实现自下而上迭代的两个关键步骤:状态转移公式推导和边界情况处理。
首先定义dp[i]为s前i字符,即区间[0,i)上解码方法的总数。
由于迭代是自下而上的,在我们求dp[i]时,其实子问题dp[i-1]和dp[i-2]已经被推导出来了。
因为一个字符被编码后其范围在"1"~"26"之间,我们需要对s[i-1],s[i-2]分情况进行分析。
s[i-1]被单独解码,如果s[i-1]在'1'~'9'范围内,可以被单独解码,这个时候被解码的数量dp[i]等于dp[i-1]。s[i-2]s[i-1]一起被解码,如果s[i-2]s[i-1]在"10"~"26"范围内,可以被组合解码,这个时候被解码的数量dp[i]等于dp[i-2]。- 如果
1和2中的条件都满足,那么被解码的数量dp[i]等于dp[i-1] + dp[i-2]。
由上面的分析可以知道状态转移公式如下:
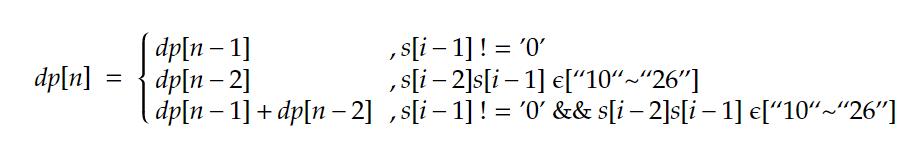
对于边界条件 dp[0] = 1,因为空字符串也可以被解码为空字符串。
C++代码
class Solution {
public:
int numDecodings(string s) {
int s_len = s.length();
vector<int> dp(s_len + 1, 0);
//边界条件处理
dp[0] = 1;
for(int i = 1; i <= s_len; ++i) {
//状态转移公式
if (s[i - 1] != '0') dp[i] = dp[i - 1];
if (i - 1 > 0 && ((s[i - 2] == '1') || (s[i - 2] == '2' && s[i - 1] >= '0' && s[i - 1] <= '6'))) {
//状态转移公式
dp[i] += dp[i - 2];
}
}
return dp[s_len];
}
};
java代码
class Solution {
public int numDecodings(String s) {
int sLen = s.length();
int[] dp = new int[sLen + 1];
// 边界条件处理
dp[0] = 1;
for (int i = 1; i <= sLen; ++i) {
// 状态转移公式
if (s.charAt(i - 1) != '0') dp[i] = dp[i - 1];
if (i - 1 > 0 && ((s.charAt(i - 2) == '1') || (s.charAt(i - 2) == '2' && s.charAt(i - 1) >= '0' && s.charAt(i - 1) <= '6'))) {
// 状态转移公式
dp[i] += dp[i - 2];
}
}
return dp[sLen];
}
}
python代码
class Solution:
def numDecodings(self, s: str) -> int:
s_len = len(s)
dp = [0] * (s_len + 1)
# 边界条件处理
dp[0] = 1
for i in range(1, s_len + 1):
# 状态转移公式
if s[i - 1] != '0':
dp[i] = dp[i - 1]
if i - 1 > 0 and (s[i - 2] == '1' or (s[i - 2] == '2' and '0' <= s[i - 1] <= '6')):
# 状态转移公式
dp[i] += dp[i - 2]
return dp[s_len]
复杂度分析
时间复杂度: O(n),n为s的长度。
空间复杂度: O(n),n为s的长度。





![[pytorch] --- pytorch基础之损失函数与反向传播](https://i-blog.csdnimg.cn/direct/d7918f0c5e0d4bc2be09bd8aaf71e61a.png)