牛客周赛 Round 58 D题

好好好数

题目背景

牛客周赛 Round 58

题目描述

样例 #1

样例输入 #1

2
60 3
114 514

样例输出 #1

2
114

做题思路

考虑到k-好数实际上是$k$进制下取0/1的操作。

而且问题也是k-好数的和，其工作原理和算进制数一样。

例如$30=3^3+3^1$ , 而$60=30+30=3^3+3^1+3^3+3^1$

实际上就是多次取60在3进制下的位数。

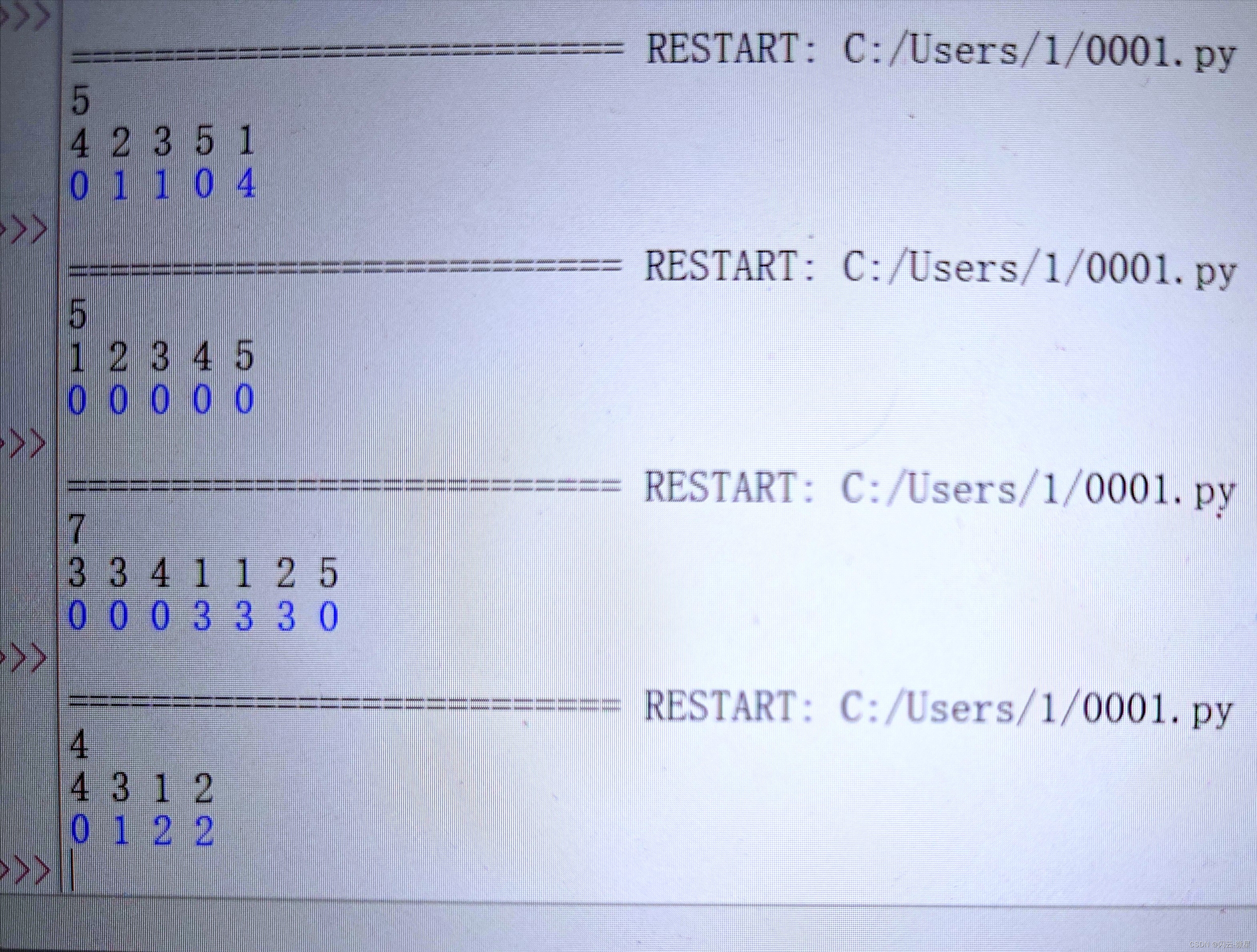
并且观察样例，进行实验，60在3进制下是$0202$，而114在514进制下是$114$

所以答案就是找$n$在$k$进制下最大的位数。

严格证明 ： 实际上每一个k-好数可以表示为若干个不同的$k$的整数次幂之和的数字。

翻译过来就是 k-好数 = {   0 / 1   } ∗ k 0 + {   0 / 1   } ∗ k 1 + {   0 / 1   } ∗ k 2 + {   0 / 1   } ∗ k 3 + . . . {   0 / 1   } ∗ k m \set{0/1}*k^0 + \set{0/1}*k^1 + \set{0/1}*k^2 + \set{0/1}*k^3 + ... \set{0/1}*k^m {0/1}∗k0+{0/1}∗k1+{0/1}∗k2+{0/1}∗k3+...{0/1}∗km

相当于每次就最多取该进制位下的一个数字。那么要最小化答案，按照贪心思想，最小需要取$n$在$k$进制下最大的位数。如果问最大的话就是所有位数和。

唯独需要注意的是$k=1$时候，因为$1^m=1$，所以$n=1^1+1^2+...+1^n$，所以只需要取一个数$n$。

代码

#include <iostream>
#define endx(x) {std::cout << x << '\n';return;}
#define int long long
using namespace std;
void solve(){
    int n,k;
    cin >> n >> k;
    if(k==1)endx(1);
    int maxa = 0;
    while(n){
       maxa = max(maxa , n%k);
        n/=k;
    }
    cout << maxa << '\n';
}
signed main(){
    int t;cin >> t;
    while(t--)solve();
    return 0;
}