判断二分图

news2024/9/22 21:30:32

题目链接

判断二分图

题目描述

注意点

graph.length == n
不存在自环（graph[u] 不包含 u）
不存在平行边（graph[u] 不包含重复值）
如果 v 在 graph[u] 内，那么 u 也应该在 graph[v] 内（该图是无向图）
这个图可能不是连通图，也就是说两个节点 u 和 v 之间可能不存在一条连通彼此的路径

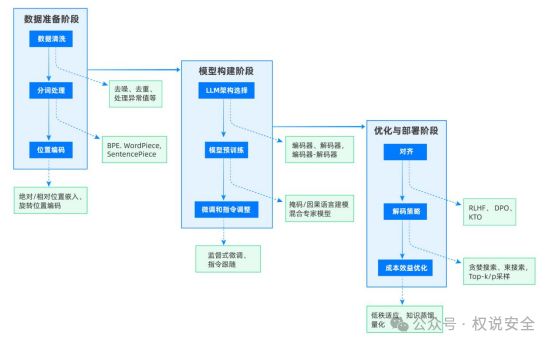
解答思路

使用广度优先遍历解决，从起始点开始，遍历其所有相邻点，起始点分第一类，其相邻点分到第二类，相邻点的相邻点又分到第一类，以此类推…如果bfs能将所有点都划分为两类，说明可以划分为二分图；如果中间某个相邻点与当前节点分在了同一类，则说明无法划分为二分图
需要注意的是图可能不是连通图，所以不能只是从第一个节点开始遍历（会漏掉未与第一个连通的节点）

代码

class Solution {
    public boolean isBipartite(int[][] graph) {
        int n = graph.length;
        // 0标识节点未分类，1表示分在第一类，-1表示分在第二类
        int[] arr = new int[n];
        Deque<Integer> dq = new ArrayDeque<>();
        for (int i = 0; i < n; i++) {
            if (arr[i] != 0) {
                continue;
            }
            arr[i] = 1;
            dq.offer(i);
            while (!dq.isEmpty()) {
                int x = dq.poll();
                int color = arr[x];
                // x点的相邻点
                for (int y : graph[x]) {
                    // 相邻点已分类且与当前节点在同一类，则无法二分
                    if (arr[y] == color) {
                        return false;
                    }
                    if (arr[y] == 0) {
                        arr[y] = -color;
                        dq.offer(y);
                    }
                }
            }
        }
        return true;
    }
}