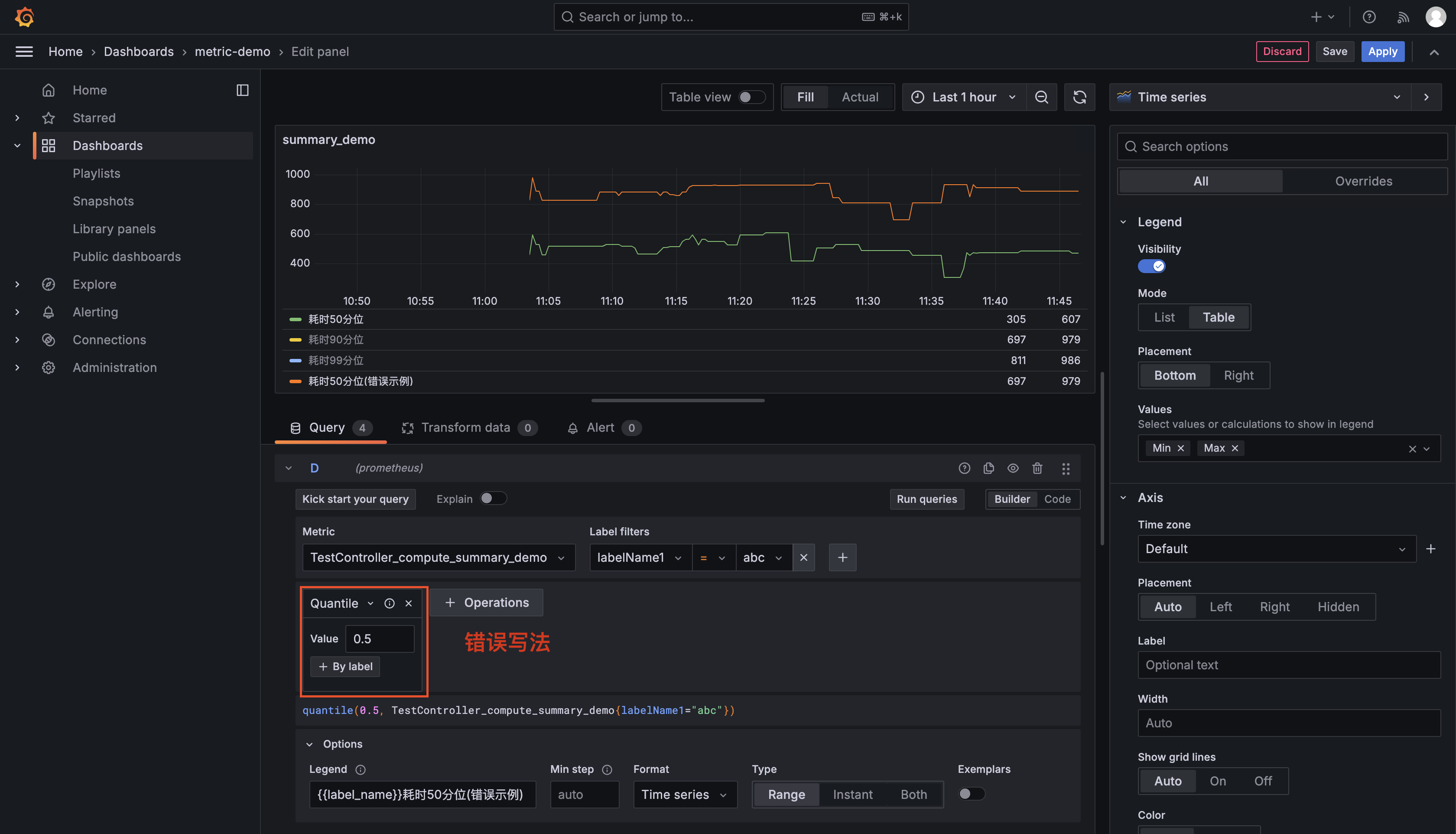
AVL树是在二叉搜索树基础上实现的，与二叉搜索树不同的是，AVL树的左右子树高度相差不超过1.

AVL树的旋转

大致分为四类：

单旋：

左左——右旋：使平衡因子为-2的父节点与左子树相连，该节点的左节点与左孩子的右节点相连

右右——左旋：使平衡因子为2的父节点与右子树相连，该节点的右节点与右孩子的左子树相连

双旋：以下是最简单的情况，具体还要考虑插入位置来改平衡因子

左右——先左旋后右旋

右左——先右旋再左旋

代码

#include<iostream>
#include<time.h>
#include<assert.h>
#include<stdlib.h>
using namespace std;
template<class T>
struct AVLtreeNode
{
	AVLtreeNode<T>* left;
	AVLtreeNode<T>* right;
	AVLtreeNode<T>* parent;
	T data;
	int bf;//平衡因子
	AVLtreeNode(const T& d)
		:left(nullptr),right(nullptr),parent(nullptr),data(d),bf(0)
	{}
};
template <class T>
class AVLtree
{
	AVLtreeNode<T>* root;
public:
	AVLtree()
		:root(nullptr)
	{}
	void insert(const T& d)
	{
		//二叉搜索树方式插入
		AVLtreeNode<T>* newt = new AVLtreeNode<T>(d);
		if (root == nullptr)
			root = newt;
		else
		{
			AVLtreeNode<T>* n = root;
			AVLtreeNode<T>* p = root;
			while (n)
			{
				p = n;
				if (n->data >= newt->data)
					n = n->left;
				else
					n = n->right;
			}
			if (p->data >= newt->data)
			{
				p->left = newt;
				newt->parent = p;
			}
			else
			{
				p->right = newt;
				newt->parent = p;
			}
		}
		//向上调整平衡因子
		
		AVLtreeNode<T>* p = newt->parent;
		AVLtreeNode<T>* n =newt;
		while (p)
		{
			assert(p);
			assert(root);
			if (p->left == n)
				p->bf--;
			else if(p->right==n)
				p->bf++;
			if (p->bf == 0)
				break;
				if (abs(p->bf) == 2)
				{
					if (p->bf == -2 && p->left->bf == -1)
					{
						if (p == root)
							root = p->left;
						p->bf = 0;
						p->left->bf = 0;
						RotateR(p);
						
					}
					else if (p->bf == 2 && p->right->bf == 1)
					{
						if (p == root)
							root = p->right;
						p->bf = 0;
						p->right->bf = 0;
						RotateL(p);
					}
					else if (p->bf == -2 )
					{
						if (p == root)
							root = p->left->right;
						int bf = p->left->right->bf;
						if (bf == -1)
						{
							p->left->right->bf = 0;
							p->left->bf = 0;
							p->bf = 1;
						}
						else if (bf == 1)
						{
							p->left->right->bf = 0;
							p->left->bf = -1;
							p->bf = 0;
						}
						else if (bf == 0)
						{
							p->left->right->bf = 0;
							p->left->bf = 0;
							p->bf = 0;
						}
						
						RotateL(p->left);
						RotateR(p);
					}
					else
					{
						if (p == root)
							root = p->right->left;
						int bf = p->right->left->bf;
						if (bf == 1)
						{
							p->right->left->bf = 0;
							p->bf = -1;
							p->right->bf = 0;
						}
						else if (bf == -1)
						{
							p->bf = 0;
							p->right->bf = 1;
							p->right->left->bf = 0;
						}
						else
						{
							p->bf = 0;
							p->right->bf = 0;
							p->right->left->bf = 0;
						}
						RotateR(p->right);
						RotateL(p);
					}
					root->parent = nullptr;
					p = p->parent;
					break;
				}
				n = p;
			p = p->parent;
		}
	}
	void show()
	{
		inor(root);
	}
	
	AVLtreeNode<T>* Find(const T& key)
	{
		AVLtreeNode<T>* cur = root;
		while (cur)
		{
			if (cur->data < key)
			{
				cur = cur->right;
			}
			else if (cur->data > key)
			{
				cur = cur->left;
			}
			else
			{
				return cur;
			}
		}

		return nullptr;
	}
	bool IsBalance()
	{
		return _IsBalance(root);
	}
};
template<typename T>
void inor(AVLtreeNode<T>* root)
{
	if (root == nullptr)
		return;
	pre(root->left);
	cout << root->data << ' ';
	pre(root->right);
}
template<typename T>
void RotateR(AVLtreeNode<T>* root)
{
	AVLtreeNode<T>* n = root->left;
	root->left = n->right;
	if(n->right)
	n->right->parent = root;
	n->right = root;
	n->parent = root->parent;
	if (root->parent != nullptr)
	{
		if (root->parent->left == root)
			root->parent->left = n;
		else
			root->parent->right = n;
	}
	root->parent = n;
}
template<typename T>
void RotateL(AVLtreeNode<T>* root)
{
	AVLtreeNode<T>* n = root->right;
	root->right = n->left;
	if(n->left)
	n->left->parent = root;
	n->left = root;
	n->parent = root->parent;
	if (root->parent != nullptr)
	{
		if (root->parent->left == root)
			root->parent->left = n;
		else
			root->parent->right = n;
	}
	root->parent = n;
}
template<typename T>
int _Height(AVLtreeNode<T>* root)
{
	if (root == nullptr)
		return 0;

	return max(_Height(root->left), _Height(root->right)) + 1;
}
template<typename T>
bool _IsBalance(AVLtreeNode<T>* root)
{
	if (root == nullptr)
		return true;

	int leftHeight = _Height(root->left);
	int rightHeight = _Height(root->right);
	// 不平衡
	if (abs(leftHeight - rightHeight) >= 2)
	{
		cout << root->data << endl;
		return false;
	}

	// 顺便检查一下平衡因子是否正确
	if (rightHeight - leftHeight != root->bf)
	{
		cout << root->data << endl;
		return false;
	}

	return _IsBalance(root->left)
		&& _IsBalance(root->right);
}
void test()
{
	int num = 100000;
	AVLtree<int> t;
	int a[] = { 37,18,52,58,72,51,42,98,34,87  };
	for (int i = 0; i < num; i++)
	{
	
		int k = rand()+1;
	/*	while (t.Find(k) != nullptr)
			k = rand()%1000000 + 1;*/

		t.insert(k);
	//cout <<i<<' '<< k << ':';

	}
	cout << t.IsBalance() << endl;


}
int main()
{
	srand(time(NULL));
	test();
}