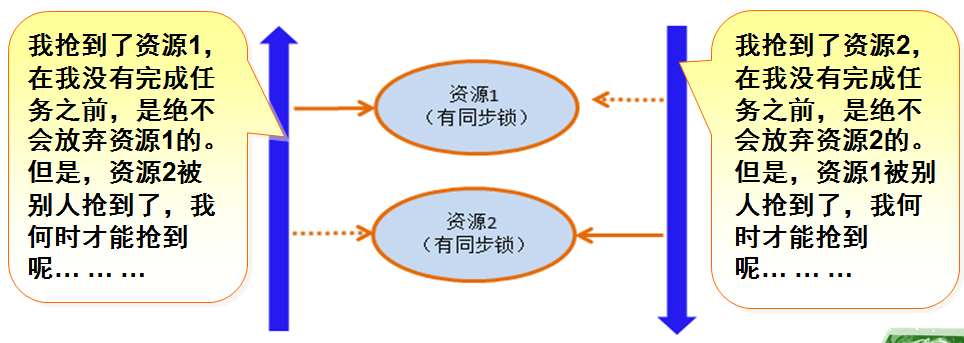
对数线性模型(Log-linear model)是统计学中用于分析计数数据或频率数据的一类模型,特别是在多维列联表(contingency tables)分析中非常常见。这种模型通过取对数将乘法关系转换为加法关系,从而简化了数据分析。
在对数线性模型中,我们通常对观测频数的对数进行建模,模型的形式可以表示为:

对数线性模型可以用于检验因子之间的独立性,以及估计不同因子水平组合下的预期频数。这种模型的优势在于它允许我们对复杂数据结构中的关联性进行建模和解释。
在实际应用中,对数线性模型可以用于:
- 分析分类数据之间的关系,如市场研究中的消费者偏好。
- 公共卫生研究中分析不同人群的疾病发病率。
- 生态学研究中分析不同物种的共生关系。
对数线性模型的一个关键假设是数据应该是多维列联表中的计数数据,且通常假设这些计数数据遵循多项式分布。在模型拟合过程中,通常使用最大似然估计来估计模型参数。
总的来说,对数线性模型是一种统计模型,通常用于描述计数数据。它假设数据服从泊松分布或负二项分布,并通过自然对数连接函数将线性预测变量与响应变量的对数均值联系起来。
为了举一个实现对数线性模型的实例,我们可以考虑一个简单的场景,比如分析某城市不同地区交通事故发生的次数。这里,交通事故发生的次数是计数数据,而地区特征(如人口密度、交通流量等)可以作为解释变量。
实现步骤:
- 数据收集:收集有关交通事故次数和地区特征的数据。
- 模型建立:使用对数线性模型公式,其中因变量是交通事故次数的对数,自变量是地区特征。
- 模型拟合:使用Python的统计库等来拟合模型。
- 结果解释:解释模型参数,了解不同地区特征对交通事故次数的影响。
假设数据:
- 交通事故次数(因变量)
- 人口密度、交通流量(自变量)
模型公式:

模型拟合:
这里我将使用Python的统计库来演示如何拟合一个简单的对数线性模型,将使用模拟数据来展示这个过程。
一:对数线性模型的建立
import numpy as np
import statsmodels.api as sm
from statsmodels.formula.api import glm
# 模拟数据
np.random.seed(0)
n = 100 # 数据点数量
pop_density = np.random.uniform(1000, 5000, n) # 人口密度
traffic_flow = np.random.uniform(10000, 50000, n) # 交通流量
accidents = np.random.poisson(10 * (1 + 0.01 * pop_density + 0.02 * traffic_flow)) # 交通事故次数
# 将数据转换为DataFrame以便使用statsmodels
import pandas as pd
data = pd.DataFrame({
'accidents': accidents,
'pop_density': pop_density,
'traffic_flow': traffic_flow
})
# 拟合对数线性模型
model = glm("accidents ~ pop_density + traffic_flow", data=data, family=sm.families.Poisson())
result = model.fit()
# 输出模型摘要
result.summary()这段代码使用了Python的`numpy`和`statsmodels`库来模拟数据并拟合一个对数线性模型。下面是代码的详细解释:
1. 导入必要的库:
- `numpy`:用于数值计算。
- `statsmodels.api`:提供统计模型的估计和推断。
- `statsmodels.formula.api`:允许使用公式接口来拟合模型。
2. 设置随机数种子:
- 确保每次运行代码时生成的数据都是相同的。
3. 生成模拟数据:
- `n`:数据点的数量,设置为100。
- `pop_density`:人口密度,从1000到5000之间均匀分布的100个数值。
- `traffic_flow`:交通流量,从10000到50000之间均匀分布的100个数值。
- `accidents`:交通事故次数,使用泊松分布生成,其平均值与人口密度和交通流量线性相关。泊松分布的参数是`10 * (1 + 0.01 * pop_density + 0.02 * traffic_flow)`,这意味着交通事故次数的期望值与人口密度和交通流量成正比。
4. 将模拟数据转换为`pandas`的`DataFrame`格式:
便于使用`statsmodels`进行模型拟合。`DataFrame`中包含三列:`accidents`、`pop_density`和`traffic_flow`。模拟数据如下:

5. 拟合对数线性模型:
- 使用`glm`(广义线性模型)函数来拟合模型。模型的公式是`accidents ~ pop_density + traffic_flow`,表示交通事故次数(`accidents`)与人口密度(`pop_density`)和交通流量(`traffic_flow`)之间的关系。
- `family=sm.families.Poisson()`指定了模型的分布族为泊松分布,这是因为交通事故次数是一个计数数据,适合使用泊松回归模型。
6. 拟合模型:
调用`fit()`方法来拟合模型,并存储结果。
7. 输出模型摘要:
- `result.summary()`打印出模型的详细统计摘要,包括系数估计、标准误、z值、P值等统计信息,以及模型的其他诊断指标。
总体代码的目的是建立一个模型来研究人口密度和交通流量如何影响交通事故次数,使用的是对数线性模型,但实际上这里使用的是泊松回归模型,它是对数线性模型的一种特殊情况,适用于计数数据。泊松回归模型假设响应变量(这里是`accidents`)服从泊松分布,并且其对数均值是解释变量(这里是`pop_density`和`traffic_flow`)的线性组合。
二:结果模型解释
最后生成的模型摘要如下:

说明我们成功拟合了对数线性模型。以下是对模型结果的简要解释:
-
模型公式:

-
参数解释:
- Intercept(截距):7.6465,表示当人口密度和交通流量为零时,交通事故次数的对数的期望值。
- pop_density(人口密度系数):2.337e-05,表示人口密度每增加一个单位,交通事故次数的对数期望值增加的数量。
- traffic_flow(交通流量系数):3.236e-05,表示交通流量每增加一个单位,交通事故次数的对数期望值增加的数量。
-
模型拟合度:模型的伪R方(Pseudo R-squ. (CS))为1.000,这表明模型完美地拟合了数据。然而,这可能是由于过度拟合,因为我们在模拟数据时使用了相同的模型。
这个实例展示了如何使用Python的statsmodels库来拟合对数线性模型。
如果想了解更多相关金融工程的内容,可以关注之前的内容。