数据结构：树形结构（树、堆）详解

news2024/9/24 3:24:00

数据结构：树形结构（树、堆）详解

  • 一、树
    • （一）树的性质
    • （二）树的种类
      • 二叉树
      • 多叉树
      • 满N叉树
      • 完全N叉树
    • （三）二叉树的实现
      • 1、二叉树结构定义
      • 2、二叉树功能实现
        • （1）前序、中序、后序、层序遍历
        • （2）二叉树结点个数
        • （3） ⼆叉树叶⼦结点个数
        • （4） 二叉树第k层结点个数
        • （5）二叉树的深度/高度
        • （6）⼆叉树查找值为x的结点
        • （7）二叉树销毁
        • （8）判断二叉树是否为完全二叉树
  • 二、堆
    • （一）堆的实现
      • 1、堆的结构定义
      • 2、堆的初始化
      • 3、向上调整操作
      • 4、向下调整操作
      • 5、入堆操作
      • 6、堆的扩容
      • 7、出堆操作
      • 8、堆的销毁
      • 9、堆的判空、查看堆顶元素
    • （二）哈夫曼编码实现
      • 结束语

一、树

树的物理结构和逻辑结构上都是树形结构

（一）树的性质

• ⼦树是不相交的
• 除了根结点外，每个结点有且仅有⼀个⽗结点
• ⼀棵N个结点的树有N-1条边

（二）树的种类

树按照根节点的分支来分，可以分为二叉树和多叉树。

二叉树

二叉树（Binary Tree）
定义：每个节点最多有两个子节点的树结构。可以是空树，或者由一个根节点和左、右子树组成。

多叉树

多叉树（Multiway Tree）
定义：每个节点可以有多个子节点的树结构，节点子节点的数量没有限制。

树按照结点的特性来观察，又可以有满N叉树和完全N叉树

满N叉树

满N叉树是一种深度为K的二叉树，其中每一层的节点数都达到了该层能有的最大节点数。

在这里插入图片描述

完全N叉树

除了最后一层外，每一层都被完全填满，并且最后一层所有节点都尽量靠左排列。

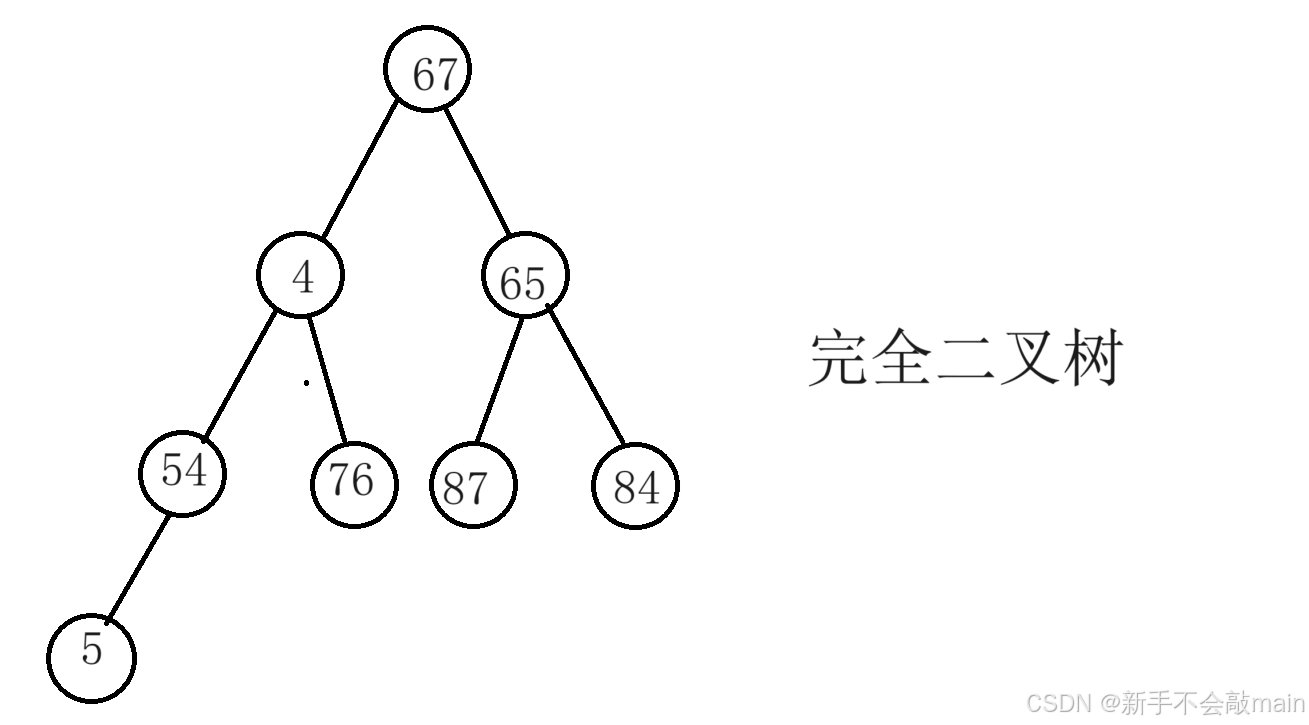
在这里插入图片描述

（三）二叉树的实现

1、二叉树结构定义

用 typedef 可以使得后面的使用范围更广

typedef int BTDataType;
typedef struct BinaryTreeNode
{
	BTDataType data;
	struct BinaryTreeNode* left;
	struct BinaryTreeNode* right;
}BTNode;

2、二叉树功能实现

（1）前序、中序、后序、层序遍历

下面的层序遍历方式采用的是一层一层的处理方式

void PreOrder(BTNode* root) {
	if (root == NULL) return;
	printf("%d ", root->data);
	PreOrder(root->left);
	PreOrder(root->right);
	return;
}

void InOrder(BTNode* root) {
	if (root == NULL) return;
	InOrder(root->left);
	printf("%d ", root->data);
	InOrder(root->right);
	return;
}

void PostOrder(BTNode* root) {
	if (root == NULL) return;
	PostOrder(root->left);
	PostOrder(root->right);
	printf("%d ", root->data);
	return;
}

void LevelOrder(BTNode* root) {
	queue<BTNode*> q;
	q.push(root);
	while (!q.empty()) {
		int num = q.size();
		for (int i = 0; i < num; i++) {
			BTNode* temp = q.front();
			if(temp->left) q.push(temp->left);
			if(temp->right) q.push(temp->right);
			printf("%d ", temp->data);
			q.pop();
		}
		printf("\n");
	}
	return;
}
（2）二叉树结点个数

两种方法都可以实现求结点个数，但是第二种需要另外创建变量接收返回值，因此第一种方式比较好

//方法一
int BinaryTreeSize(BTNode* root) {
	if (root == NULL) return 0;
	return 1 + BinaryTreeSize(root->left) +
	 BinaryTreeSize(root->right);
}

//方法二
void BinaryTreeSize(BTNode* root, int* psize) {
	if (root == NULL) return;
	if (root->left) {
		(*psize)++;
		BinaryTreeSize(root->left, psize);
	}
	if (root->right) {
		(*psize)++;
		BinaryTreeSize(root->right, psize);
	}
	return;
}
（3） ⼆叉树叶⼦结点个数

只需要统计叶子结点即可，和求普通结点个数相似

int BinaryTreeLeafSize(BTNode* root) {
	if (root == NULL) return 0;
	if (root->left == NULL && root->right == NULL) return 1;
	return BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right);
}
（4） 二叉树第k层结点个数

需要加一个二叉树层数的变量

int BinaryTreeLevelKSize(BTNode* root, int k) {
	if (root == NULL) return 0;
	if (k == 1) return 1;
	return BinaryTreeLevelKSize(root->left, k - 1) + BinaryTreeLevelKSize(root->right, k - 1);
}
（5）二叉树的深度/高度
int BinaryTreeDepth(BTNode* root) {
	if (root == NULL) return 0;
	int a = BinaryTreeDepth(root->left);
	int b = BinaryTreeDepth(root->right);
	return (a > b ? a : b) + 1;
}
（6）⼆叉树查找值为x的结点

如果没有找到，不要忘记返回空

BTNode* BinaryTreeFind(BTNode* root, BTDataType x) {
	if (root == NULL) return NULL;
	if (root->data == x) return root;
	BTNode* left = BinaryTreeFind(root->left, x);
	if (left) return left;
	BTNode* right = BinaryTreeFind(root->right, x);
	if (right) return right;
	return NULL;
}
（7）二叉树销毁

采用二级指针的方式传入，可以避免函数处理后在进行置空处理。

void BinaryTreeDestory(BTNode** root) {
	if (*root == NULL) return;
	BinaryTreeDestory(&((*root)->left));
	BinaryTreeDestory(&((*root)->right));
	free(*root);
	*root = NULL;
	return;
}
（8）判断二叉树是否为完全二叉树

这段代码是老夫目前想了许久，觉得很有不错的代码，先不考虑它的实现复杂度以及简洁程度，它实现的功能不错，可以将二叉树包括空结点放在队列之中，自己觉得很好，哈哈，也许你没看到这句，那我就放心了。

bool BinaryTreeComplete(BTNode* root) {
	queue<BTNode*> q;
	BinaryTreePushQueue(root, q);
	while (!q.empty()) {
		if (q.front() != NULL) q.pop();
		else break;
	}
	while (!q.empty()) {
		if (q.front() == NULL) q.pop();
		else return false;
	}
	return true;
}

void BinaryTreePushQueue(BTNode* root, queue<BTNode*>& q) {
	vector<vector<BTNode*>> v;
	BinaryNodePushVector(root, v, 0);
	for (int i = 0; i < v.size(); i++) {
		for (auto x : v[i]) {
			q.push(x);
		}
	}
	return;
}

void BinaryNodePushVector(BTNode* root, vector<vector<BTNode*>>& v, int k) {
	if (v.size() == k) v.push_back(vector<BTNode*>());
	if (root == NULL) {
		v[k].push_back(NULL);  //如果不处理空结点，取消这步即可
		return;
	}
	v[k].push_back(root);
	BinaryNodePushVector(root->left, v, k + 1);
	BinaryNodePushVector(root->right, v, k + 1);
	return;
}

二、堆

堆的物理结构是一段连续空间，但是逻辑机构是树形结构

（一）堆的实现

1、堆的结构定义

下面通过宏函数来实现交换，可以使得交换简便，或者用指针也行。

typedef int HeapDataType;

typedef struct Heap {
	HeapDataType* __data;
	HeapDataType* data;
	int count;
	int capacity;
}Heap;

#define SWAP(a ,b){\
	HeapDataType c = (a);\
	(a) = (b);\
	(b) = (c);\
}

2、堆的初始化

用偏移量的方式，节约了内存。
从数组下标为1开始分配结点，使得后面求父节点，左右孩子运算和逻辑更简单

void HeapInit(Heap* pHeap) {
	assert(pHeap);
	pHeap->__data = (HeapDataType*)malloc(sizeof(HeapDataType));
	pHeap->data = pHeap->__data - 1;
	pHeap->capacity = 1;
	pHeap->count = 0;
	return;
}

3、向上调整操作

可以使用递归或者是循环来实现向上调整

void Heap_UP_Update(Heap* pHeap, int i) {
	assert(pHeap);
	while (FATHER(i) >= 1 && pHeap->data[FATHER(i)] > pHeap->data[i]) {
		SWAP(pHeap->data[FATHER(i)], pHeap->data[i]);
		i = FATHER(i);
	}
	return;
}

void DG_Heap_UP_Update(Heap* pHeap, int i) {
	assert(pHeap);
	if (FATHER(i) < 1) return;
	if (pHeap->data[FATHER(i)] > pHeap->data[i]) {
		SWAP(pHeap->data[FATHER(i)], pHeap->data[i]);
		i = FATHER(i);
		DG_Heap_UP_Update(pHeap, i);
	}
	return;
}

4、向下调整操作

void Heap_DOWN_Update(Heap* pHeap, int i) {
	assert(pHeap);
	int size = pHeap->count - 1;
	while (LEFT(i) <= size) {
		int l = LEFT(i), r = RIGHT(i), ind = i;
		if (pHeap->data[ind] > pHeap->data[l]) ind = l;
		if (r <= size && pHeap->data[ind] > pHeap->data[r]) ind = r;
		if (ind == i) break;
		SWAP(pHeap->data[i], pHeap->data[ind]);
		i = ind;
	}
	return;
}

5、入堆操作

void HeapPush(Heap* pHeap, HeapDataType x) {
	assert(pHeap);
	HeapCheckCapacity(pHeap);
	pHeap->data[pHeap->count + 1] = x;
	DG_Heap_UP_Update(pHeap, pHeap->count + 1);
	pHeap->count += 1;
	return;
}

6、堆的扩容

void HeapCheckCapacity(Heap* pHeap) {
	assert(pHeap);
	if (pHeap->capacity == pHeap->count) {
		HeapDataType* temp = (HeapDataType*)realloc(pHeap->__data, 2 * pHeap->capacity * sizeof(HeapDataType));
		if (!temp) {
			perror("Heap Realloc Fail!");
			exit(1);
		}
		pHeap->__data = temp;
		pHeap->capacity *= 2;
	}
	return;
}

7、出堆操作

void HeapPop(Heap* pHeap) {
	assert(pHeap);
	assert(!HeapEmpty(pHeap));
	pHeap->data[1] = pHeap->data[pHeap->count];
	Heap_DOWN_Update(pHeap, 1);
	pHeap->count -= 1;
	return;
}

8、堆的销毁

void HeapDestroy(Heap* pHeap) {
	assert(pHeap);
	free(pHeap->__data);
	pHeap->data = NULL;
	pHeap->__data = NULL;
	pHeap->capacity = 0;
	pHeap->count = 0;
	return;
}

9、堆的判空、查看堆顶元素

int HeapEmpty(Heap* pHeap) {
	assert(pHeap);
	return pHeap->count == 0;
}

HeapDataType HeapTop(Heap* pHeap) {
	assert(!HeapEmpty(pHeap));
	return pHeap->data[1];
}

（二）哈夫曼编码实现

#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
#include<stdlib.h>
#include<time.h>
#include<string.h>
#include<algorithm>
#include<unordered_map>
#include<vector>
using namespace std;

#define FATHER(i) ((i) / 2)
#define LEFT(i) ((i) * 2)
#define RIGHT(i) ((i) * 2 + 1)

typedef struct Node {
	char* c;
	int freq;
	struct Node* lchild, * rchild;
}Node;

template<typename T>
void Swap(T& a, T& b) {
	T c = a;
	a = b;
	b = c;
	return;
}

//void swap(Node* a, Node* b) {
//	Node* c = a;
//	a = b;
//	b = c;
//	return;
//}

Node* getNewNode(int freq,const char* c) {
	Node* p = (Node*)malloc(sizeof(Node));
	p->freq = freq;
	p->c = _strdup(c);
	p->lchild = p->rchild = NULL;
	return p;
}

void clear(Node* root) {
	if (root == NULL) return;
	clear(root->lchild);
	clear(root->rchild);
	free(root);
	return;
}

typedef struct heap {
	Node** data, **__data;
	int size, count;
}heap;

heap* initHeap(int n) {
	heap* p = (heap*)malloc(sizeof(heap));
	p->__data = (Node**)malloc(sizeof(Node*) * n);
	p->data = p->__data - 1;
	p->size = n;
	p->count = 0;
	return p;
}

int empty(heap* h) {
	return h->count == 0;
}

int full(heap* h) {
	return h->count == h->size;
}

Node* top(heap* h) {
	if (empty(h)) return NULL;
	return h->data[1];
}

//void up_update(Node** data, int i) {
//	while (FATHER(i) >= 1) {
//		int ind = i;
//		if (data[i]->freq < data[FATHER(i)]->freq) {
//			swap(data[i], data[FATHER(i)]);
//		}
//		if (ind == i) break;
//		i = FATHER(i);
//	}
//	return;
//}

void up_update(Node** data, int i) {
	while (i > 1 && data[i]->freq < data[FATHER(i)]->freq) {
		Swap(data[i], data[FATHER(i)]);
		i = FATHER(i);
	}
	return;
}

void down_update(Node** data, int i, int n) {
	while (LEFT(i) <= n) {
		int ind = i, l = LEFT(i), r = RIGHT(i);
		if (data[i]->freq > data[l]->freq) ind = l;
		if (RIGHT(i) <= n && data[r]->freq < data[ind]->freq) ind = r;
		if (ind == i) break;
		Swap(data[ind], data[i]);
		i = ind;
	}
	return;
}

void push(heap* h, Node* node) {
	if (full(h)) return;
	h->count += 1;
	h->data[h->count] = node;
	up_update(h->data, h->count);
	return;
}

void pop(heap* h) {
	if (empty(h)) return;
	h->data[1] = h->data[h->count];
	h->count -= 1;
	down_update(h->data, 1, h->count);
	return;
}

void clearHeap(heap* h) {
	if (h == NULL) return;
	free(h->__data);
	free(h);
	return;
}

Node* build_huffman_tree(Node** nodeArr, int n) {
	heap* h = initHeap(n);
	for (int i = 0; i < n; i++) {
		push(h, nodeArr[i]);
	}
	Node* node1, * node2;
	int freq;
	for (int i = 1; i < n; i++) {
		node1 = top(h);
		pop(h);
		node2 = top(h);
		pop(h);
		freq = node1->freq + node2->freq;
		Node* node3 = getNewNode(freq, "0");
		node3->lchild = node1;
		node3->rchild = node2;
		push(h, node3);
	}
	return h->data[1];
}

void output(Node* root) {
	if (root == NULL) return;
	output(root->lchild);
	//if (root->lchild == NULL && root->rchild == NULL) 
		printf("%s : %d\n", root->c, root->freq);
	output(root->rchild);
	return;
}

char charArr[100];
unordered_map<char*, char*> h;

void extract_huffman_code(Node* root, int i) {
	charArr[i] = 0;
	if (root->lchild == NULL && root->rchild == NULL) {
		h[root->c] = _strdup(charArr);
		return;
	}
	charArr[i - 1] = '0';
	extract_huffman_code(root->lchild, i + 1);
	charArr[i - 1] = '1';
	extract_huffman_code(root->rchild, i + 1);
	return;
}


int main() {
#define MAX_CHAR 26
	//1.首先用一个数组读取相关字符串及其频率
	Node** charArr = (Node**)malloc(sizeof(Node*)*MAX_CHAR);
	char arr[10];
	int freq;
	for (int i = 0; i < MAX_CHAR;i++) {
		scanf("%s%d", arr, &freq); 
		charArr[i] = getNewNode(freq, arr);
	}

	//2.建立哈夫曼树
	Node* root = build_huffman_tree(charArr, MAX_CHAR);

	//3.提取哈夫曼编码进入unordered_map
	extract_huffman_code(root, 1);

	//4.将unordered_map转换成vector排序，可以按照字典序输出编码
	vector<pair<char*, char*>> v(h.begin(), h.end());
	sort(v.begin(), v.end(), [&](const pair<char*, char*>& a, const pair<char*, char*>& b) {
		return strcmp(a.first, b.first) < 0;
		});
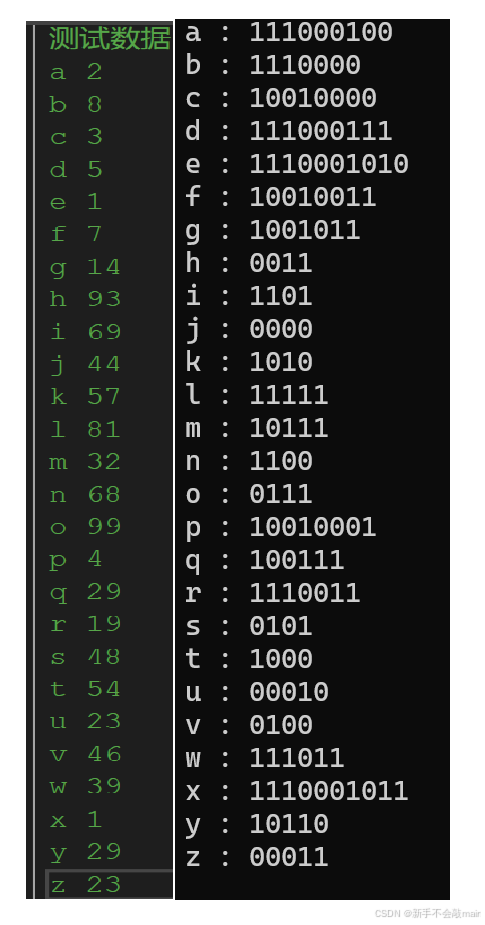
	for (auto& x : v) {
		printf("%s : %s\n", x.first, x.second);
	}
	return 0;
}

在这里插入图片描述

结束语

关注博主的专栏，博主会分享更多的数据结构知识！
🐾博主的数据结构专栏

在这里插入图片描述

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/2093761.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

数字化转型中的数据应用：挑战、机遇与追赶之路

数字化转型中的数据应用：挑战、机遇与追赶之路

在数字化时代的大潮中&#xff0c;数据已悄然从企业的边缘资源跃升为最宝贵的核心资产。然而&#xff0c;这场数据盛宴并未带来普遍的数据应用成熟&#xff0c;反而揭示了企业在数据利用上的巨大鸿沟。即便是全球500强企业&#xff0c;在数据应用的征途上&#xff0c;也仅仅是比…
阅读更多...
秋招突击——笔试总结——8/31——京东笔试

秋招突击——笔试总结——8/31——京东笔试

文章目录 引言正文第一题——下一个字典序的字符个人实现 第二题——冒泡排序的变种个人实现空间复杂度比较低的版本 第三题——两人走路个人实现 总结 引言 今天京东笔试做的并不好&#xff0c;有很多问题的关窍都没有找到&#xff0c;所以在很多问题上都浪费了大量的时间&am…
阅读更多...
JVM下篇：性能监控与调优篇-04-JVM运行时参数

JVM下篇：性能监控与调优篇-04-JVM运行时参数

文章目录 4. JVM 运行时参数4.1. JVM 参数选项4.1.1. 类型一&#xff1a;标准参数选项4.1.2. 类型二&#xff1a;-X 参数选项4.1.3. 类型三&#xff1a;-XX 参数选项 4.2. 添加 JVM 参数选项4.3. 常用的 JVM 参数选项4.3.1. 打印设置的 XX 选项及值4.3.2. 堆、栈、方法区等内存…
阅读更多...
Java多线程（二）线程同步

Java多线程（二）线程同步

1、线程同步问题 当多个线程同时操作同一个数据时&#xff0c;就会产生线程同步问题。 为了确保在任何时间点一个共享的资源只被一个线程使用&#xff0c;使用了“同步”。当一个线程运行到需要同步的语句后&#xff0c;CPU不去执行其他线程中的、可能影响当前线程中的下一句代…
阅读更多...
记一次学习--webshell绕过（动态检测）

记一次学习--webshell绕过（动态检测）

目录 第一种样本 代码分析 第二种样本 代码分析 题目分析 结果 不断学习&#xff0c;不断进步 快就是慢&#xff0c;慢就是快。审视自身 第一种样本 <?php class xxxd implements IteratorAggregate {public $xxx "system";public function __construct(…
阅读更多...
C++ | Leetcode C++题解之第388题文件的最长绝对路径

C++ | Leetcode C++题解之第388题文件的最长绝对路径

题目&#xff1a; 题解&#xff1a; class Solution { public:int lengthLongestPath(string input) {int n input.size();int pos 0;int ans 0;vector<int> level(n 1);while (pos < n) {/* 检测当前文件的深度 */int depth 1;while (pos < n && in…
阅读更多...
R语言统计分析——单因素协方差分析

R语言统计分析——单因素协方差分析

参考资料&#xff1a;R语言实战【第2版】 单因素协方差分析&#xff08;ANCONA&#xff09;扩展了单因素方差分析&#xff08;ANOVA&#xff09;&#xff0c;包含一个或多个定量的协变量。下面使用multcomp包中的litter数据集进行操作&#xff1a; # 加载数据集 data(litter,p…
阅读更多...
0-HDMI高速接口协议基础介绍

0-HDMI高速接口协议基础介绍

高清多媒体接口(HDMI&#xff0c;High Definition Multimedia Interface)是一种数字化视频/音频接 口技术&#xff0c;是适合影像传输的专用型数字化接口&#xff0c;其可同时传送音频和视频信号&#xff0c;同时无需在 信号传送前进行数/模或者模/数转换。从2002年HDMI发布最初…
阅读更多...
Windows 环境nginx安装使用及目录结构详解

Windows 环境nginx安装使用及目录结构详解

一、 Windows 环境nginx安装及基本使用 1、下载 nginx-1.27.1 最新的主线版本 安装 nginx/Windows&#xff0c;请下载1.27.1最新的主线版本&#xff0c; nginx 的主线分支包含所有已知的修复程序。 2、 解压缩 nginx-1.27.1 版本 nginx/Windows 作为标准控制台应用程序&#x…
阅读更多...
YOLO | YOLO目标检测算法（分类、检测、分割）

YOLO | YOLO目标检测算法（分类、检测、分割）

github&#xff1a;https://github.com/MichaelBeechan CSDN&#xff1a;https://blog.csdn.net/u011344545 分类、检测、分割 思考&#xff1a;计算机视觉能够解决哪些问题&#xff1f;&#xff1f;&#xff1f;&#xff1f;分类、检测、分割 分割&#xff1a;语义分割和实例分…
阅读更多...
SOMYO™——将“照片”转为“手绘素描”的专业级软件

SOMYO™——将“照片”转为“手绘素描”的专业级软件

一定要往下看&#xff0c;最精彩的在最后哦&#xff01; 1 关于素描的几句话 素描是西方美术的灵魂。值得为自己、亲人与好友留下一张别致的素描。 素描的定义&#xff1a;艺术家通过线条的粗细、浓淡、疏密等变化&#xff0c;试图精准地再现形态的体感、质感和动感的艺术…
阅读更多...
轻量级进程(LWP)和线程

轻量级进程(LWP)和线程

线程是CPU调度的基本单位 进程是承担系统资源的基本实体(进程是资源分配的基本单位) 线程并不拥有系统资源,而是共享使用进程的资源,进程的资源由系统进行分配 任何一个线程都可以创建或撤销另一个线程 多进程里&#xff0c;子进程可复制父进程的所有堆和栈的数据&#xff1b…
阅读更多...
黑神话悟空-提高画质、防卡顿、修复等各种功能、各种CT表、各种存档、武器包、人物、装备替换等193+MOD合集

黑神话悟空-提高画质、防卡顿、修复等各种功能、各种CT表、各种存档、武器包、人物、装备替换等193+MOD合集

193MOD合集&#xff0c;提高画质&#xff0c;减少卡顿、修复等功能MOD各种CT表各种存档武器包、物品、人物、装备、造型替换等 具体MOD可在文件内查看 特别说明&#xff1a;3款珍品大圣套装替换初始套装MOD是不同的&#xff0c;&#xff08;其中全装备珍品大圣套装是不可以跳出…
阅读更多...
笔记 12 ： 彭老师课本第 6 章， PWM ，代码实践

笔记 12 ： 彭老师课本第 6 章， PWM ，代码实践

&#xff08;85&#xff09; 驱动写多了&#xff0c;会发现&#xff0c;首先就是硬件的初始化&#xff0c;配置硬件。 &#xff08;86&#xff09;查看源代码组织&#xff1a; &#xff08;87&#xff09; 编译过程不变&#xff1a; &#xff08;88&#xff09; 运行同以前的步…
阅读更多...
2024年8月总结及随笔之逝

2024年8月总结及随笔之逝

1. 回头看 日更坚持了609天。 读《零信任网络&#xff1a;在不可信网络中构建安全系统》更新完成读《软件开发安全之道&#xff1a;概率、设计与实施》开更并持续更新 2023年至2024年8月底累计码字1463007字&#xff0c;累计日均码字2402字。 2024年8月码字109278字&#x…
阅读更多...
全网最适合入门的面向对象编程教程：42 Python常用复合数据类型-collections容器数据类型

全网最适合入门的面向对象编程教程：42 Python常用复合数据类型-collections容器数据类型

全网最适合入门的面向对象编程教程&#xff1a;42 Python 常用复合数据类型-collections 容器数据类型 摘要&#xff1a; 在 Python 中&#xff0c;collections 模块提供了一组高效、功能强大的容器数据类型&#xff0c;扩展了内置的基础数据类型&#xff08;如 list、tuple、…
阅读更多...
ubuntu14.04.5出现配环境后重启进不了图形化界面解决记录

ubuntu14.04.5出现配环境后重启进不了图形化界面解决记录

前言 这段时间给公司接了一个需要使用到linux环境进行交叉编译的工程&#xff0c;就采用了简单易操作的图形化ubuntu系统。 镜像采用的是&#xff1a;ubuntu14.04.5-desktop-amd64.iso(官网下载的&#xff09; 配置环境的过程下载了众多依赖包&#xff0c;总之就是缺啥下载啥…
阅读更多...
Mac 安装 jdk 8详细教程

Mac 安装 jdk 8详细教程

Mac 电脑上安装Jdk 8 的步骤很简单&#xff0c;不用想Windows那样需要配置环境变量PATH、JAVA_HOME。 具体方法如下&#xff1a; 首先&#xff0c;去JDK官网下载对应版本的JDK 8。 这里需要注册一个账号&#xff0c;然后&#xff0c;账号下载。 下载完后&#xff0c;得到一个…
阅读更多...
【IEEE独立出版 | 往届快至会后2个月检索】2024年第四届电子信息工程与计算机科学国际会议(EIECS 2024，9月27-29)

【IEEE独立出版 | 往届快至会后2个月检索】2024年第四届电子信息工程与计算机科学国际会议(EIECS 2024，9月27-29)

2024年第四届电子信息工程与计算机科学国际会议&#xff08;EIECS 2024&#xff09;将于2024年9月27日至29日在中国延吉举行。会议由长春理工大学主办&#xff0c;延边大学、长春理工大学电子信息工程学院、长春理工大学计算机学院、长春理工大学人工智能学院承办&#xff0c;多…
阅读更多...
视频智能分析厨帽检测算法，厨帽检测算法全套源码、样本和模型展示

视频智能分析厨帽检测算法，厨帽检测算法全套源码、样本和模型展示

厨帽检测算法是一种基于人工智能和计算机视觉技术的系统&#xff0c;旨在自动检测厨师是否佩戴了符合规范的厨帽。该算法通过分析视频流或图像数据&#xff0c;实时识别厨帽的佩戴情况&#xff0c;从而帮助餐饮企业确保员工的着装符合卫生标准。这一技术广泛应用于餐馆、厨房、…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023