1.7 离散频率
离散时间和采样率
模拟到数字转换器 (ADC) 对连续时间信号进行采样以生成离散时间样本。对于数字信号处理器来说,该信号仅存储在内存中作为一系列数字。因此,采样率 F S F_S FS 的知识是数字域中信号处理的关键。
对于时间而言,可以轻松确定存储在内存中的此类信号的周期或频率。例如,图 1.44 中的正弦波的周期 T T T 很明显是 10 个样本,而采样时间 T S = 1 F S T_S = \frac{1}{F_S} TS=FS1 可用于以秒为单位找到其周期。
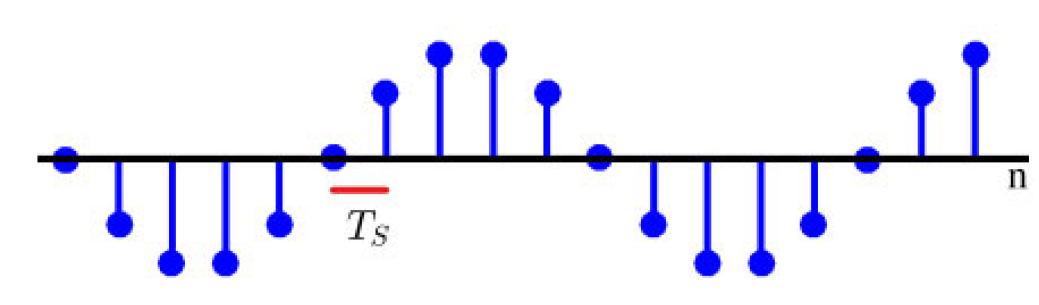
图 1.44:离散时间正弦波
- 对于采样率
F
S
=
10
F_S = 10
FS=10 Hz,
T
S
=
0.1
T_S = 0.1
TS=0.1 秒,因此
T = 10 samples period × 0.1 seconds/sample = 1 second T = \frac{10 \text{ samples}}{\text{period}} \times 0.1 \text{ seconds/sample} = 1 \text{ second} T=period10 samples×0.1 seconds/sample=1 second
其频率为 F = 1 T = 1 F = \frac{1}{T} = 1 F=T1=1 Hz。 - 对于采样率
F
S
=
500
F_S = 500
FS=500 Hz,
T
S
=
0.002
T_S = 0.002
TS=0.002 秒,因此
T = 10 samples period × 0.002 seconds/sample = 0.02 seconds T = \frac{10 \text{ samples}}{\text{period}} \times 0.002 \text{ seconds/sample} = 0.02 \text{ seconds} T=period10 samples×0.002 seconds/sample=0.02 seconds
其频率为 F = 1 T = 50 F = \frac{1}{T} = 50 F=T1=50 Hz。
如前所述,这两种正弦波的样本都将存储在内存中,离散域内没有区别。
离散频率和采样率
假设以采样率 F S = 1 T S F_S = \frac{1}{T_S} FS=TS1 采集了总共 N N N 个样本,这样就在时间上跨越了 N T S N T_S NTS 秒的持续时间。因此,这些 N N N 个样本所能表示的最低频率是由一个完整周期的正弦波完成的——而不再表示小于此间隔 N T S N T_S NTS 秒的任何其他周期。于是,其频率为 1 ( N T S ) \frac{1}{(N T_S)} (NTS)1 Hz,并表示为:
$$I \rightarrow V_I[n] = \cos 2\pi \frac{1}{N T_S} \cdot t = \cos 2\pi \frac{1}{N} \cdot \frac{1}{T_S} \cdot n$$$$Q \uparrow V_Q[n] = \sin 2\pi \frac{1}{N T_S} \cdot t = \sin 2\pi \frac{1}{N} \cdot \frac{1}{T_S} \cdot n$$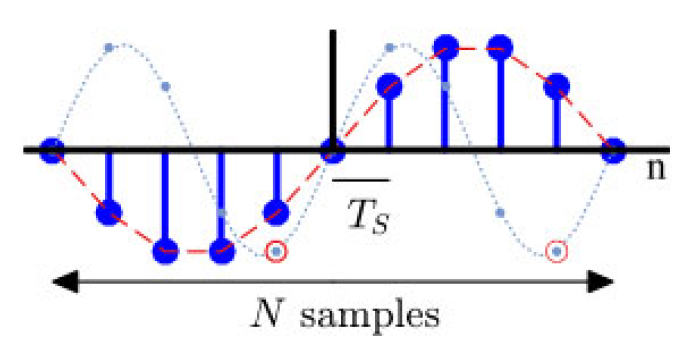
图 1.45:两个离散时间正弦波的 Q 部分
- 其中一个有 N N N 个样本,离散频率为 1 N \frac{1}{N} N1 ;
- 另一个频率为 2 N \frac{2}{N} N2 。
因此, 1 N \frac{1}{N} N1 是该正弦波的离散频率,其 Q 部分如图 1.45 所示。
现在考虑以下方程:
$$\frac{1}{N T_S} = \frac{F_S}{N} = F_S \cdot \frac{1}{N}$$并观察以下内容:
- 实际频率为 F S ( 1 N ) F_S \left( \frac{1}{N} \right) FS(N1),但离散频率为 1 N \frac{1}{N} N1。
- 由这种离散设置中可以表示的最低频率决定的频率分辨率为 F S N \frac{F_S}{N} NFS。
- 视为 F S ⋅ 1 N F_S \cdot \frac{1}{N} FS⋅N1 时,我们可以得到更多的离散频率样本,这些样本是 1 N \frac{1}{N} N1 的整数倍。
因此,所有这些复数正弦波的频率都是基频 1 N \frac{1}{N} N1 的整数倍。图 1.45 背景中画有虚线的 Q 组件的 2 N \frac{2}{N} N2 的示例显示,在这些 N N N 个样本中有两个周期,这意味着每个 N N N 样本有 2 个周期,或每个样本有 2 N \frac{2}{N} N2 个周期。
进一步扩展这个概念,复数正弦波的离散频率为 k N \frac{k}{N} Nk,在 N N N 个样本的间隔内完成 k k k 个周期(或每个样本 k / N k/N k/N 个周期)。
正交性
我们称频率为 1 N \frac{1}{N} N1 和 2 N \frac{2}{N} N2 的正弦波分别为 A 和 B。正如我们现在看到的那样,它们是相互正交的。正交性意味着在零移处的相关性为零。换句话说,它们样本对样本积的总和为零。对于一个实数正弦波来说,
$$\sum_{n=0}^{N-1} \sin \left( 2\pi \frac{1}{N} n \right) \cdot \sin \left( 2\pi \frac{2}{N} n \right) = 0 \tag{1.46}$$这一点可以从图 1.45 中得到验证。注意 B 在 N N N 个样本中有 2 个周期。在第一个周期中,B 的样本与 A 的负样本相乘。
其第二个周期中,相同的乘积与正号的 A A A 样本具有完全相同的幅度。通过这种方式,这个和为零。
从图 1.45 中画的两个样本的圆可以看出这一点。验证正弦波 A A A 的相应样本具有相反的符号。由于 DSP 的原始工作原理是复数正弦波而不是实数正弦波,因此我们现在在该上下文中分析正交性。
由于第二个信号的共轭,结果的 I I I 项为 I ⋅ I + Q ⋅ Q I \cdot I + Q \cdot Q I⋅I+Q⋅Q,而 Q Q Q 项的结果为 Q ⋅ I − I ⋅ Q Q \cdot I - I \cdot Q Q⋅I−I⋅Q。对于两个离散频率为 k / N k/N k/N 和 k ′ / N k'/N k′/N 的复数正弦波,滞后 0 处的相关性是:
$$I \rightarrow \sum_{n=0}^{N-1} \left[\cos\frac{2\pi k}{N}n \cdot \cos\frac{2\pi k'}{N}n + \sin\frac{2\pi k}{N}n \cdot \sin\frac{2\pi k'}{N}n \right]$$$$Q \uparrow \sum_{n=0}^{N-1} \left[\sin\frac{2\pi k}{N}n \cdot \cos\frac{2\pi k'}{N}n - \cos\frac{2\pi k}{N}n \cdot \sin\frac{2\pi k'}{N}n \right]$$使用等式 cos A cos B + sin A sin B = cos ( A − B ) \cos A \cos B + \sin A \sin B = \cos(A - B) cosAcosB+sinAsinB=cos(A−B) 和 sin A cos B − cos A sin B = sin ( A − B ) \sin A \cos B - \cos A \sin B = \sin(A - B) sinAcosB−cosAsinB=sin(A−B),
$$I \rightarrow \sum_{n=0}^{N-1} \cos \frac{2\pi (k-k')}{N} n = \begin{cases} N & k=k' \\ 0 & k\neq k' \end{cases}$$$$Q \uparrow \sum_{n=0}^{N-1} \sin \frac{2\pi (k-k')}{N} n = 0$$我们利用了样本和的事实, cos ( ⋅ ) \cos(\cdot) cos(⋅) 和 sin ( ⋅ ) \sin(\cdot) sin(⋅) 在 N N N 样本内具有整数个周期,因此为零。此外,当 k = k ′ k = k' k=k′ 时, cos ( 0 ) = 1 \cos(0) = 1 cos(0)=1。这个概念在图 1.46 中进行了说明。
我们已经证明了以下结果:
“所有具有频率为基本频率 F s ( 1 / N ) F_s(1/N) Fs(1/N) 整数倍的复数正弦波彼此正交。”
离散频率轴
对于具有 N N N 个离散时间域样本,是否存在无限的复数正弦波彼此正交?答案是否定的,我们认为它们的数量仅为 N N N。为了验证这一点,让我们探索一个离散频率 N / N = 1 N/N = 1 N/N=1 的选项。
$$\sin\frac{2\pi N}{N}n = \sin 2\pi n = 0$$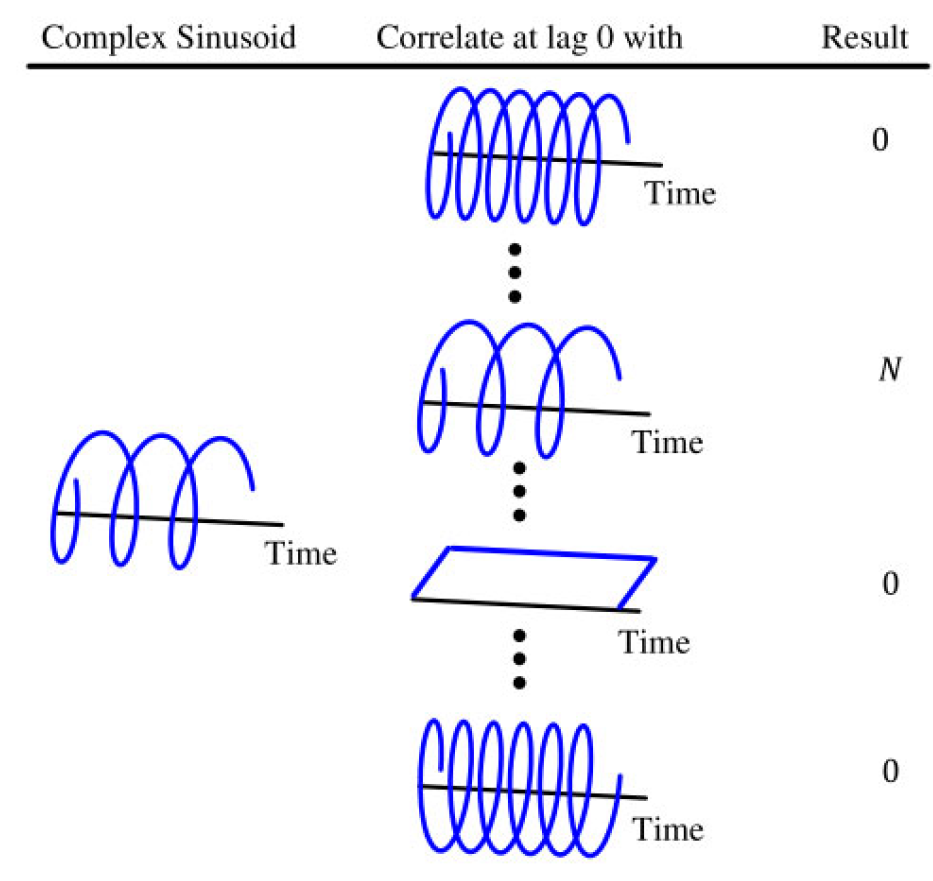
图 1.46:在 N N N 个样本中,离散频率为 k / N k/N k/N 的复数正弦波与任何其他离散频率为 k ′ ≠ k k' \neq k k′=k 的复数正弦波正交。
因此,离散频率为 0 的复数正弦波与离散频率为 1 的复数正弦波相同。对于下一个候选者 ( N + 1 ) / N (N+1)/N (N+1)/N,使用 sin ( A + B ) = sin A cos B + cos A sin B \sin(A+B) = \sin A \cos B + \cos A \sin B sin(A+B)=sinAcosB+cosAsinB:
$$\sin\left(2\pi\frac{N+1}{N}n\right) = \sin\left(2\pi n \cos 2\pi \frac{1}{N}n\right) + \cos\left(2\pi n \sin 2\pi \frac{1}{N}n\right) = \sin\left(2\pi \frac{1}{N}n\right)$$因为 sin ( 2 π n ) = 0 \sin(2\pi n) = 0 sin(2πn)=0 且 cos ( 2 π n ) = 1 \cos(2\pi n) = 1 cos(2πn)=1。我们得出结论,从 0 到 N − 1 N-1 N−1(或者 − N / 2 -N/2 −N/2 到 N / 2 − 1 N/2 - 1 N/2−1,正如我们将很快看到的那样)只有 N N N 个不同的频率。接下来,它们只会重复自己。
在离散时间域中有 N N N 个样本时,离散频率域中也有 N N N 个样本!这些 N N N 个样本代表了复数正弦波的离散频率,这些频率是一个基本频率 1 / N 1/N 1/N 的整数倍,因此它们彼此正交。
从上面找到的 N N N 个离散频率中,我们可以构造一个离散频率轴,其成员如下:
$$0, \frac{1}{N}, \dots, \frac{N-1}{N}$$它们完全相同:
$$-1, -1+\frac{1}{N}, \dots, -\frac{1}{N}$$由于它们的周期性。然而,由于采样定理,我们选择了以 0 为中心的坐标轴。第 1.5 节中的公式 (1.36) 表明,在对信号进行采样后,连续频率 F F F 的唯一范围是:
− 0.5 F s ≤ F < + 0.5 F s -0.5F_s \leq F < +0.5F_s −0.5Fs≤F<+0.5Fs
$$-0.5 \leq \frac{F}{F_s} < +0.5 \tag{1.48}$$由于存在 N N N 个离散频率, − 0.5 ≤ F F s < + 0.5 -0.5 \leq \frac{F}{F_s} < +0.5 −0.5≤FsF<+0.5 被分成 N N N 个相等的区间(假设 N N N 是偶数),通过在以下时刻采样得到:
$$-0.5, -0.5+\frac{1}{N}, \dots, -\frac{1}{N}, 0, \frac{1}{N}, \dots, +0.5-\frac{1}{N} \tag{1.49}$$以获得离散频率轴。显然,离散频率分辨率是 1 / N 1/N 1/N。因此,离散频率基本上是基带中在 N N N 个等间隔频率点上采样的频谱内容(术语 +0.5 是由于坐标轴的周期性,实际上是 -0.5)。
公式 (1.49) 也可以写成:
$$-\frac{N/2}{N}, -\frac{N/2-1}{N}, \dots, -\frac{1}{N}, 0, \frac{1}{N}, \dots, \frac{N/2-1}{N} \tag{1.50}$$因此,离散频率轴的索引 k k k 给出为 [ − N / 2 , N / 2 − 1 ] [-N/2, N/2-1] [−N/2,N/2−1],或:
$$k = -\frac{N}{2}, -\frac{N}{2}+1, \dots, -1, 0, 1, \dots, \frac{N}{2}-1$$$$\frac{k}{N} = -0.5, -0.5+\frac{1}{N}, \dots, 0, \frac{1}{N}, \dots, +0.5-\frac{1}{N}$$这是在图 1.47 中绘制的。将上述公式与公式 (1.48) 进行比较,我们得出了离散频率 k / N k/N k/N 与连续频率 F F F 之间的关系为:
$$\frac{k}{N} = \frac{F}{F_s} \tag{1.51}$$公式 (1.51) 中离散频率 k / N k/N k/N 的单位是:
$$\text{周期/秒} \div \text{样本/秒} = \text{周期/样本}$$注释 1.8 离散频率轴
公式 (1.51) 是数字信号处理中两个最基本的关系之一,另一个是采样定理公式 (1.37)。这些是连续和离散世界之间的两个接口。
在频率域中,作为存储在处理器存储器中的一系列数字。
如果对连续和离散频率域有疑问,请参考公式 (1.51)!

图 1.47:在频域中对轴进行采样
如果已知离散频率 k N \frac{k}{N} Nk 和采样率 F S F_S FS,则实际连续频率可以通过公式 (1.51) 计算:
$$F = F_S \cdot \frac{k}{N}$$例如,设 F S = 3 F_S = 3 FS=3 kHz 且 N = 32 N = 32 N=32,
- 当 k = 0 k = 0 k=0 时, F = 3000 ⋅ 0 32 = 0 F = 3000 \cdot \frac{0}{32} = 0 F=3000⋅320=0 Hz
- 当 k = 1 k = 1 k=1 时, F = 3000 ⋅ 1 32 = 93.75 F = 3000 \cdot \frac{1}{32} = 93.75 F=3000⋅321=93.75 Hz
- 当 k = 2 k = 2 k=2 时, F = 3000 ⋅ 2 32 = 187.5 F = 3000 \cdot \frac{2}{32} = 187.5 F=3000⋅322=187.5 Hz
因此,每个 k k k 都称为频率桶(frequency bin) ,而值 N N N 决定了输入样本的数量和离散频率域的分辨率。理解公式 (1.37) 和公式 (1.51) 将使进一步的概念更容易掌握。
总之,唯一离散频率 k N \frac{k}{N} Nk 的范围是:
$$-0.5 \leq \frac{k}{N} < +0.5 \tag{1.52}$$这一组复数正弦波在图 1.48 中绘制,突出显示了离散频率索引 k k k 的旋转方向。负 k k k 的索引表示顺时针旋转方向,而正 k k k 的索引表示逆时针旋转方向。请注意,当 k N \frac{k}{N} Nk 从 -0.5 增加到 0 时,离散时间信号的振荡频率减小;而当 k N \frac{k}{N} Nk 从 0 增加到 +0.5 时,振荡频率增加。记住, k N = − 0.5 \frac{k}{N} = -0.5 Nk=−0.5 与 k N = + 0.5 \frac{k}{N} = +0.5 Nk=+0.5 是相同的。
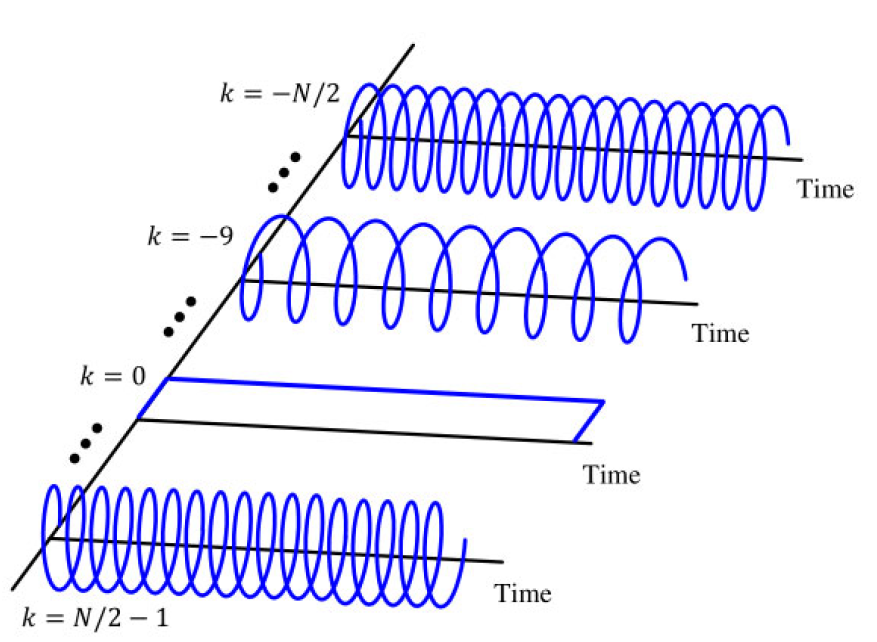
图 1.48:绘制的复数正弦波,用于突出显示左侧的离散频率轴 k k k
有些人更习惯于使用二维图形而不是三维图形。因此,这组包含 I 和 Q 分量的复数正弦波在图 1.49 中显示,设 N = 8 N = 8 N=8。
以下是该图中的一些关键观察:
- 对于 k = 0 k = 0 k=0,I 正弦波为 1,因为 cos 0 = 1 \cos 0 = 1 cos0=1,而 Q 正弦波为 0,因为 sin 0 = 0 \sin 0 = 0 sin0=0。
- 与 k = 1 k = 1 k=1 类似,I 和 Q 波形 cos 2 π ⋅ 1 N \cos 2\pi \cdot \frac{1}{N} cos2π⋅N1 和 sin 2 π ⋅ 1 N \sin 2\pi \cdot \frac{1}{N} sin2π⋅N1 在 N = 8 N = 8 N=8 个样本内完成一个完整的周期,每个具有离散频率 k N \frac{k}{N} Nk 的复数正弦波在 N 个样本的区间内跨越 k 个完整周期。
- 对于负值的 k k k,I 正弦波保持不变,而 Q 正弦波则改变符号。在复数正弦波的上下文中,这与顺时针旋转的负频率定义相符。
- 最后,要理解离散频率“周期/样本”的单位含义,请考虑图中 k = 2 k = 2 k=2 的情况。注意对于 N = 8 N = 8 N=8,离散频率等于 k N = 2 8 = 1 4 \frac{k}{N} = \frac{2}{8} = \frac{1}{4} Nk=82=41 周期/样本。请注意,这个正弦波在从一个样本到下一个样本之间完成了四分之一的周期,因此频率为 1/4 周期/样本。
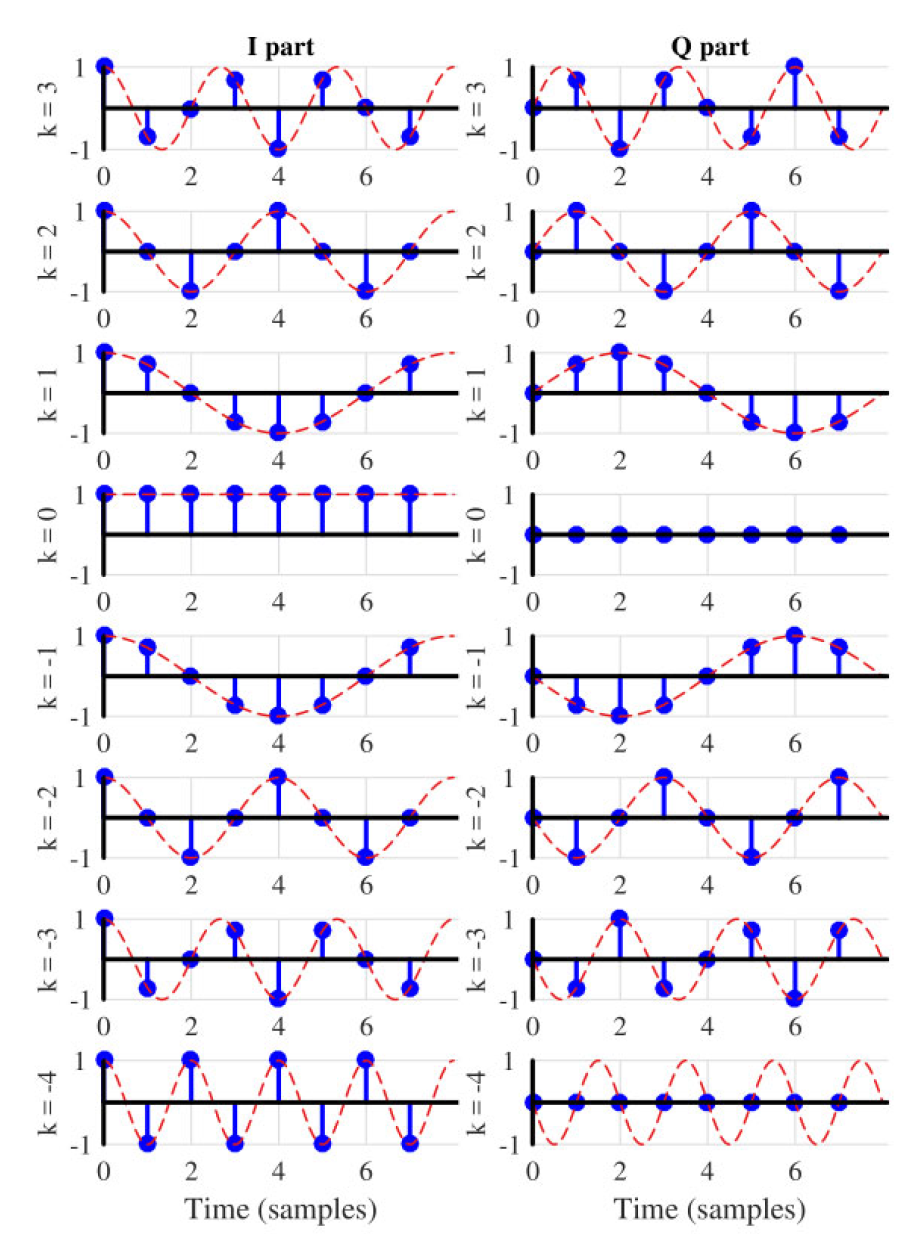
图 1.49:N = 8 个复正弦波,其频率在离散频率轴上形成“刻度”
示例 1.4
考虑一个信号
$$s(t) = 2\cos(2\pi 1000t) + 7\sin(2\pi 3000t) + 3\cos(2\pi 6000t)$$很明显,该信号中存在的连续频率为 F 1 = 1 kHz F_1 = 1 \text{kHz} F1=1kHz、 F 2 = 3 kHz F_2 = 3 \text{kHz} F2=3kHz 和 F 3 = 6 kHz F_3 = 6 \text{kHz} F3=6kHz。由于最大频率为 6 kHz,采样定理给出奈奎斯特率为 2 × 6 kHz = 12 kHz 2 \times 6 \text{kHz} = 12 \text{kHz} 2×6kHz=12kHz。
现在假设该信号以 F s = 5 kHz F_s = 5 \text{kHz} Fs=5kHz 采样,则折叠频率为 0.5 F s = 2.5 kHz 0.5F_s = 2.5 \text{kHz} 0.5Fs=2.5kHz。以等间隔 t = n T s t = nT_s t=nTs 对信号进行采样,得到
$$s[n] = s(t) |_{t=nT_s} = s \left(\frac{n}{F_s}\right) = 2\cos 2\pi \frac{1}{5} n + 7\sin 2\pi \frac{3}{5} n + 3\cos 2\pi \frac{6}{5} n = 2\cos 2\pi \frac{1}{5} n + 7\sin 2\pi \left(1 - \frac{2}{5}\right) n + 3\cos 2\pi \left(1 + \frac{1}{5}\right) n$$其中的调整是为了将所有离散频率限制在 − 0.5 -0.5 −0.5 到 0.5 之间。接下来,
$$s[n] = 2\cos 2\pi \frac{1}{5} n + 7\sin 2\pi \left(-\frac{2}{5}\right) n + 3\cos 2\pi \left(\frac{1}{5}\right) n = 5\cos 2\pi \frac{1}{5} n - 7\sin 2\pi \frac{2}{5} n$$如果将该信号在连续时间域中重建,则存在的频率为 k / N = 1 / 5 k/N = 1/5 k/N=1/5 和 k / N = − 2 / 5 k/N = -2/5 k/N=−2/5。从等式(1.51)可以看出,它们作为连续频率出现在 F 1 = 5 × 1 / 5 = 1 kHz F_1 = 5 \times 1/5 = 1 \text{kHz} F1=5×1/5=1kHz 和 5 × − 2 / 5 = − 2 kHz 5 \times -2/5 = -2 \text{kHz} 5×−2/5=−2kHz。由于只有 1 kHz 小于 0.5 F s 0.5F_s 0.5Fs 且在无混叠范围内,因此采样后仍存在。其他两个频率高于折叠频率,因此被混叠到 F 2 − F s = 3 − 5 = − 2 kHz F_2 - F_s = 3 - 5 = -2 \text{kHz} F2−Fs=3−5=−2kHz 和 F 3 − F s = 6 − 5 = 1 kHz F_3 - F_s = 6 - 5 = 1 \text{kHz} F3−Fs=6−5=1kHz。
在此有两点补充说明:
- 通过 IQ 标记法处理复数有几个优点。例如,它可以避免像 exp ( j θ ) \exp(j\theta) exp(jθ) 这样的标准复数表达式,虽然要付出额外数学运算的代价。更重要的是,它描述了数学运算在实际电子电路中的实现方式。此外,它提醒我们相位在信号分析中同样重要。
- 在本文中,每次我写涉及离散频率的表达式时,我都将其表示为 2 π k N n 2\pi \frac{k}{N}n 2πNkn 或 2 π ( k / N ) n 2\pi(k/N)n 2π(k/N)n,而不是大多数文本中使用的 2 π k n / N 2\pi kn/N 2πkn/N。前者清楚地表示了离散频率 k / N k/N k/N 的存在,类似于 2 π F t 2\pi Ft 2πFt 中的变量 F F F,而后者容易丢失这种意义。







![[米联客-XILINX-H3_CZ08_7100] FPGA程序设计基础实验连载-21读写I2C接口EEPROM实验](https://i-blog.csdnimg.cn/direct/3ee5a49e65664a999f91edab85ac63d1.png)