微信公众号上线,搜索公众号小灰灰的FPGA,关注可获取相关源码,定期更新有关FPGA的项目以及开源项目源码,包括但不限于各类检测芯片驱动、低速接口驱动、高速接口驱动、数据信号处理、图像处理以及AXI总线等

本节目录
一、单位冲激响应
1、离散系统的单位冲激响应
2、连续系统的单位冲激响应
二、时域卷积定理
本节内容
一、单位冲激响应
1、离散系统的单位冲激响应
一个系统,在输入端输入信号,在输出端会得到相应的输出信号。
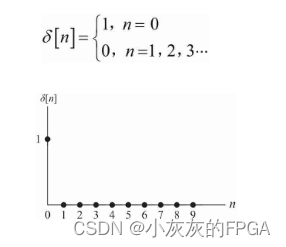
单位冲激序列δ[n]的表达式和图如下;
把δ[n]作为输入信号输入离散系统,其对应的输出信号就是单位冲激响应序列h[n]。

离散系统的输出y[n]等于输入序列x[n]和单位冲激响应序列的卷积h[n]。
y[n]=x[n]h[n],其中表示卷积。
如何理解?
系统输入δ[n]时对应的输出为h[n],输入δ[n-k]时对应的输出为h[n-k],将x[n]分解为一系列δ[n-k]之和:
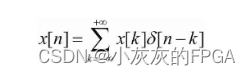
x[k]×δ[n-k]对应的输出为x[k]×h[n-k]
将其所有的输出叠加就可得到输出y[n]:
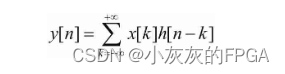
图解说明:
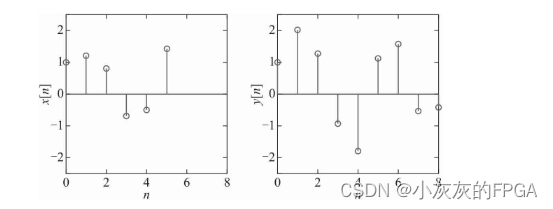
下图左为输入序列x[n],下图右为单位冲激响应序列h[n]
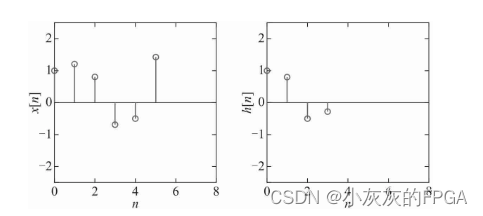
x[k]×δ[n-k]对应的输出为x[k]×h[n-k],其中k∈[0,5]
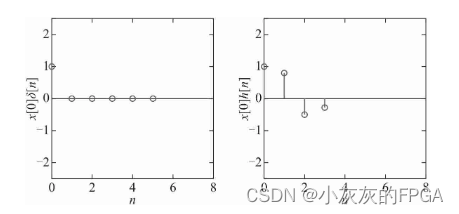
k=0,下图左为x[0]×δ[n],下图右为对应的输出为x[0]×h[n]
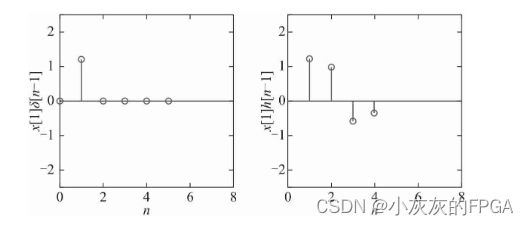
k=1,下图左为x[1]×δ[n-1],下图右为对应的输出为x[1]×h[n-1]
k=2到k=4依次类推
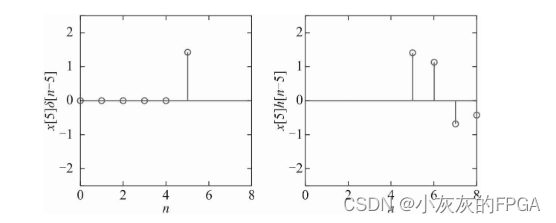
k=5,下图左为x[5]×δ[n-5],下图右为对应的输出为x[5]×h[n-5]
将所有的输出叠加,即可得到y[n]
y[n]=x[0]×h[n]+x[1]×h[n-1]+x[2]×h[n-2]+x[3]×h[n-3]+x[4]×h[n-4]+x[5]×h[n-5]
下图左为x[n],下图右为对应的输出为y[n]
2、连续系统的单位冲激响应
把单位冲激信号δ(t)作为输入信号输入连续系统,则对应的输出被称为单位冲激响应,用符号h(t)来表示。
连续系统的输出也是等于输入信号和单位冲激响应的卷积:
y(t)=x(t)*h(t)
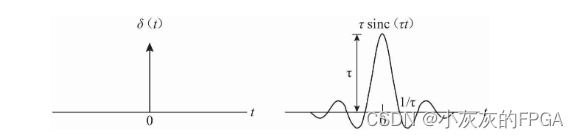
单位冲激信号输入理想低通滤波器,其输出为一个sinc信号。
将抽样信号分解成一系列冲激信号之和,每个冲激信号会在理想低通滤波器的输出端产生一个冲激响应,将所有冲激响应叠加起来就可以得到输出信号。
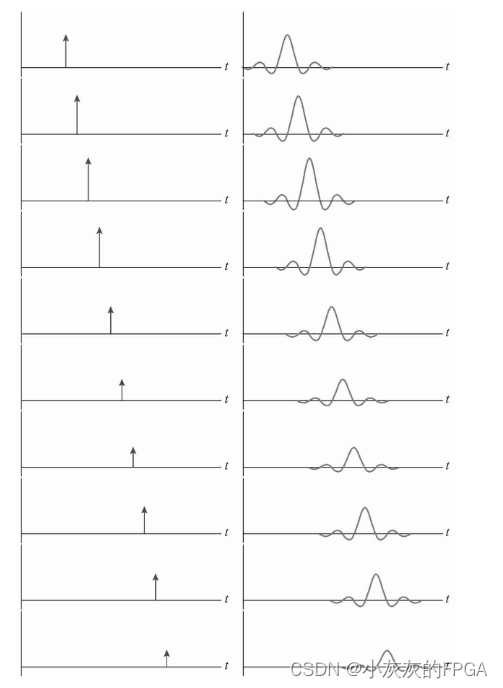
下图图左为采样的模拟信号,右图为所有冲激响应叠加结果,当冲激响应的间隔足够小时,叠加结果就是所谓的原始模拟信号。

二、时域卷积定理
两个信号做卷积,相当于在频域做乘法,这就是时域卷积定理。
若y(t)=x(t)*h(t),则Y(f)=X(f)H(f)
X(f)是输入信号x(t)的傅里叶变换;
Y(f)是输入信号y(t)的傅里叶变换;
H(f)是系统单位冲激响应δ(t)的傅里叶变换,系统的频率响应。
时域卷积定理的推导过程:
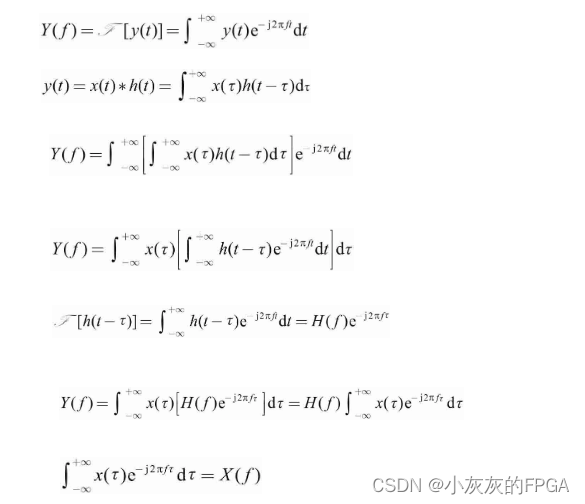
最终得到结果:Y(f)=X(f)H(f)
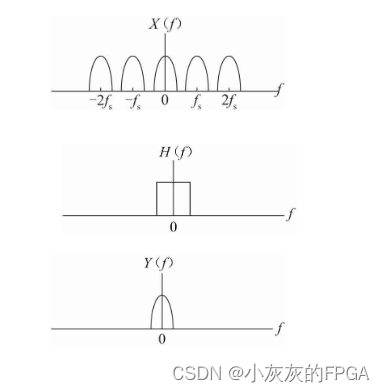
根据时域卷积定理,滤波器输出信号的频谱等于输入信号的频谱和滤波器频率响应的乘积。输入的抽样信号的频谱X(f)是由原始模拟信号频谱以采样频率为间隔进行周期性拓展得到的,X(f)与理想低通滤波器的频率响应H(f)相乘,就可以得到原始模拟信号的频谱。
下图最上方为抽样信号的频谱X(f),中间为理想低通滤波器的频率响应H(f),最下方为输出的频谱Y(f)。