✨✨ 欢迎大家来到贝蒂大讲堂✨✨
🎈🎈养成好习惯,先赞后看哦~🎈🎈
所属专栏:C++学习
贝蒂的主页:Betty’s blog
1. 位图的引入
首先我们来看一道面试题:
给40亿个不重复的无符号整数,没排过序。给一个无符号整数,如何快速判断一个数是否在这40亿个数中?
我们可能会提出以下思路:
- 遍历直接查找。
- 排序+二分查找。
- 利用红黑树或哈希表,即
set与unordered_set查找。
但是以上方法明显是错误的,因为对于40亿个整型来说有160亿byte,需要大概16G的内存空间(
1
G
=
1024
M
B
=
1024
∗
1024
K
B
=
1024
∗
1024
∗
1024
b
y
t
e
≈
10
亿
b
y
t
e
1G=1024MB=1024*1024KB=1024*1024*1024byte≈10亿byte
1G=1024MB=1024∗1024KB=1024∗1024∗1024byte≈10亿byte)。我们不可能直接向内存这么大的空间,即使放在文件中每次处理一小部分效率也是极低的。为了解决这个问题,就要用到我们接下来要将的位图——bitset。
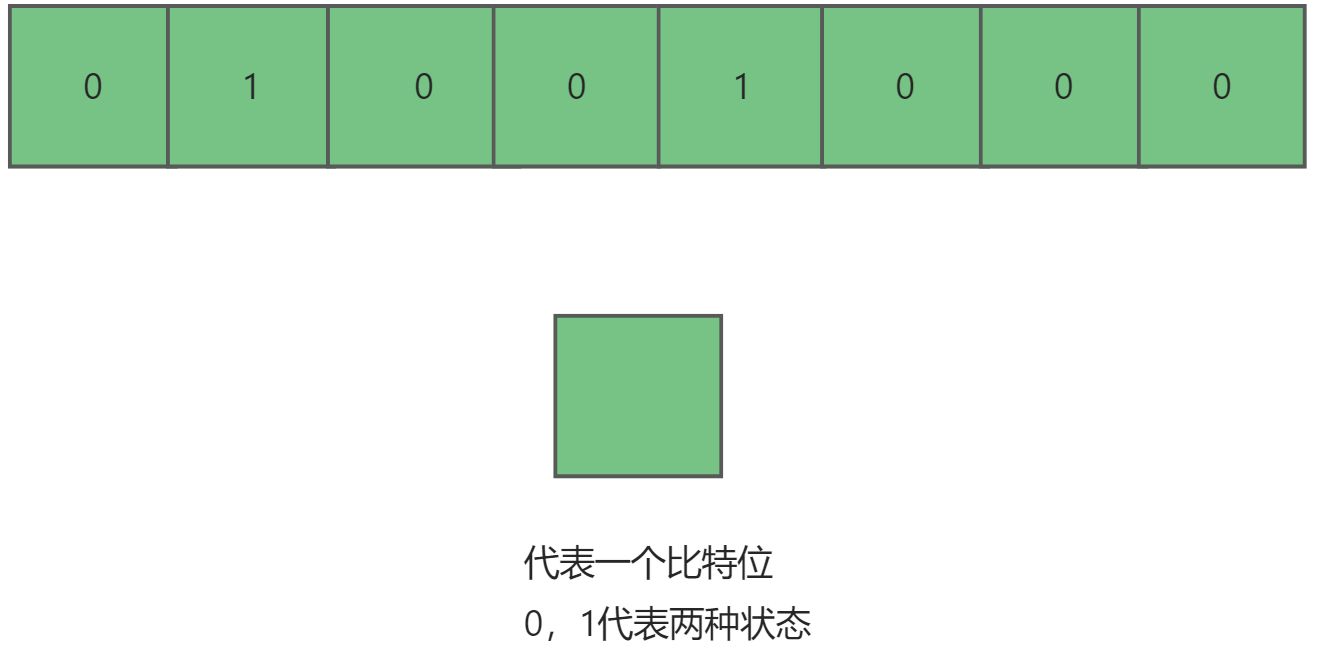
2. 位图的概念
位图(bitset),就是用一个个比特位来存放某种状态,适用于海量数据,数据无重复的场景。通常是用来判断某个数据存不存在的。
然后解决上面这道问题,我们就可以利用二进制序列中的0和1代表某个无符号整数是否存在,其中无符号整数的最大值是
2
32
−
1
2^{32}-1
232−1,即需要4294967295个比特位,大概512MB空间,这个空间大小就是我们可以接受的。
其中C++就为了我们提供了一个位图的模版类——位图
3. 位图的使用
3.1 位图的初始化
位图的初始化需要调用去构造函数,一般而言我们常用的就是以下几个接口
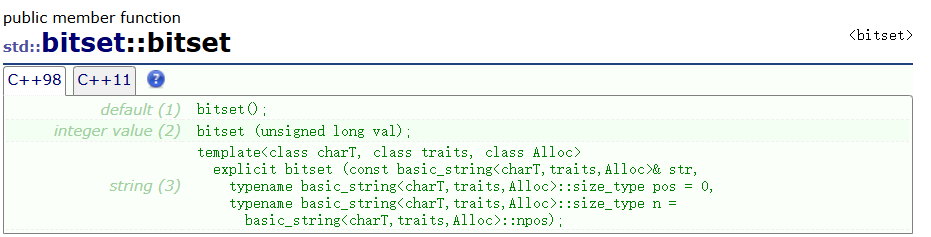
void Test1()
{
//创建一个8位的位图,其所有位默认为0
bitset<8> bit1;//000000000
//创建一个16位的位图,其所有位设置为1
bitset<16> bit2(0xffff);//1111111111111111
//利用字符串初始化
bitset<8> bit3(string("10010010"));//10010010
}
3.2 位图的成员函数
以下是位图的常见的成员函数,并且位图一般都重载了流插入<<以及流提取>>运算符。
| 成员函数 | 功能 |
|---|---|
| set | 设置指定位或所有位 |
| reset | 清空指定位或所有位 |
| flip | 反转指定位或所有位 |
| test | 获取指定位的状态 |
| count | 获取被设置位的个数 |
| size | 获取可以容纳的位的个数 |
| any | 如果有任何一个位被设置则返回 true |
| none | 如果没有位被设置则返回 true |
| all | 如果所有位都被设置则返回 true |
| [] | 返回对应位置的比特位数字 |
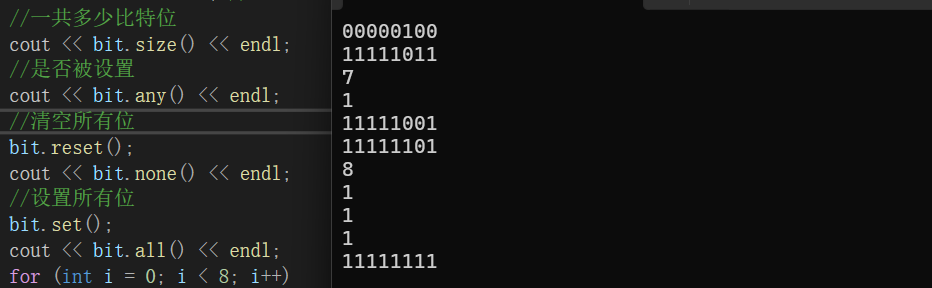
void Test2()
{
bitset<8> bit;
bit.set(2); //设置第2位
cout << bit << endl; //00000100
bit.flip(); //反转所有位
cout << bit << endl; //11111011
//被设置的个数
cout << bit.count() << endl;
//获取指顶位的状态
cout << bit.test(5) << endl;
bit.reset(1); //清空第1位
cout << bit << endl; //11111001
bit.flip(2); //反转第2位
cout << bit << endl; //11111101
//一共多少比特位
cout << bit.size() << endl;
//是否被设置
cout << bit.any() << endl;
//清空所有位
bit.reset();
cout << bit.none() << endl;
//设置所有位
bit.set();
cout << bit.all() << endl;
for (int i = 0; i < 8; i++)
{
//获取指定位的状态
cout << bit[i];
}
cout << endl;
}
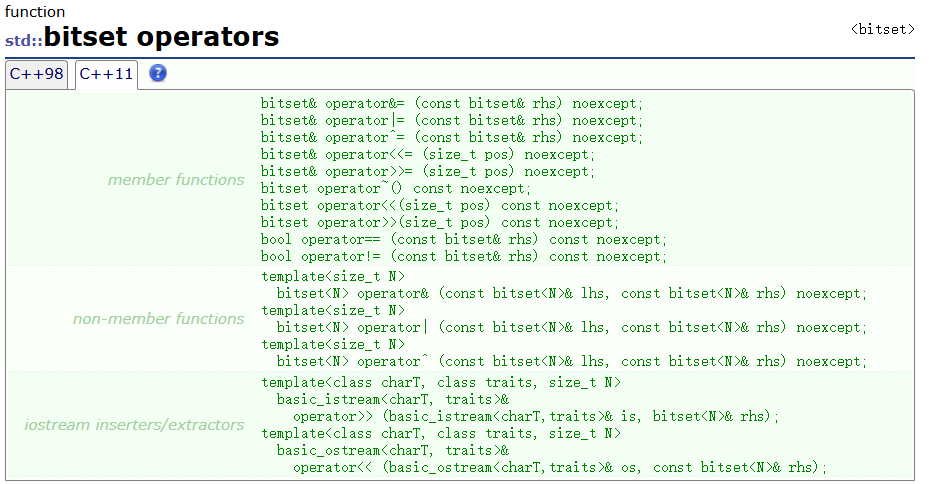
3.3 位图的位操作
除此之外,位图还重载了大多数移位操作符方便我们使用
void Test3()
{
bitset<8> bs1(string("10101010"));
bitset<8> bs2(string("10101010"));
bs1 >>= 1;
cout << bs1 << endl; //01010101
cout << (bs1 & bs2) << endl; //00000000
cout << (bs1 | bs2) << endl; //11111111
cout << (bs1 ^ bs2) << endl; //11111111
bs2 |= bs1;
cout << bs2 << endl; //11111111
}

4. 实现bitset
4.1 位图的结构
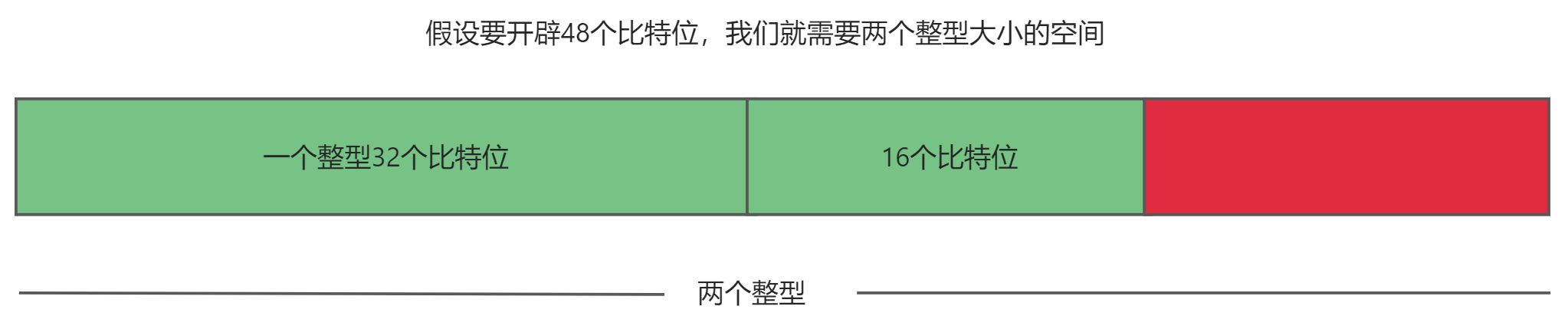
接下来我们来实现一下bitset的基本功能,首先bitset被定义为模版类,有一个非类型模版参数N,单位为比特位。然后成员变量我们可以利用一个整型数组来实现,一个整型有32个比特位,所以一般需要N/32+1个整型。
template<size_t N>
class bitset
{
public:
//构造函数
bitset();
//设置位
void set(size_t pos);
//清空位
void reset(size_t pos);
//反转位
void flip(size_t pos);
//获取位的状态
bool test(size_t pos);
//获取可以容纳的位的个数
size_t size();
//获取被设置位的个数
size_t count();
//判断位图中是否有位被设置
bool any();
//判断位图中是否全部位都没有被设置
bool none();
//判断位图中是否全部位都被设置
bool all();
private:
vector<int> _bits; //位图
};
4.2 位图的初始化
位图初始化即通过构造函数将开辟的整型空间的比特位全部设为0,即整型设为0。
//构造函数
bitset()
{
_bits.resize(N / 32 + 1, 0);
}
4.3 位图的位设置
位图我们可以先通过N%32计算修改的整型位置i,然后通过N%32得到修改的比特位的位置j。最后通过对应的位运算改变对应比特位的状态。
其中将对应比特位设置为1的运算为_bits[i] |= (1 << j)。
//设置位
void set(size_t pos)
{
assert(pos < N);
int i = pos / 32;//第几个整型
int j = pos % 32;//第几个比特位
_bits[i] |= (1 << j);
}
其中将对应比特位设置为0的运算为_bits[i] &= ~(1 << j)。
//清空位
void reset(size_t pos)
{
assert(pos < N);
int i = pos / 32;//第几个整型
int j = pos % 32;//第几个比特位
_bits[i] &= ~(1<< j);
}
其中将对应比特位翻转的运算为_bits[i] ^= (1 << j)。
void flip(size_t pos)
{
assert(pos < N);
int i = pos / 32;//第几个整型
int j = pos % 32;//第几个比特位
_bits[i] ^= (1 << j);
}
其中将对应比特位的状态运算为_bits[i] & (1 << j)。
//获取位的状态
bool test(size_t pos)
{
assert(pos < N);
int i = pos / 32;//第几个整型
int j = pos % 32;//第几个比特位
if (_bits[i] & (1 << j))
{
return true;
}
return false;
}
4.4 位图的其他操作
首先是获得位图的容量,直接返回对应的模版参数即可。
//获取可以容纳的位的个数
size_t size()
{
return N;
}
接下来我们可以获取设置的位数,首先我们得知道num&num-1能将二进制最右侧的1去掉。
//获取被设置位的个数
size_t count()
{
size_t cnt = 0;
for (int i = 0; i < N / 32 + 1; i++)
{
//取每个整数
int num = _bits[i];
while (num)
{
num = num & (num - 1);
++cnt;
}
}
return cnt;
}
接下来就是判断位图中有没有位被设置,即判断每个整型是否为0,为0就没被设置,非0就已被设置。
//判断位图中是否有位被设置
bool any()
{
for (int i = 0; i < N / 32 + 1; i++)
{
int num = _bits[i];
if (num != 0)
{
return true;
}
}
return false;
}
//判断位图中是否全部位都没有被设置
bool none()
{
return !any();
}
接下来我们判断是否全部位都被设置,我们可以先判断前N个是否设置如果全部被设置,那么其按位取反一定等于0,再取第N+1的每个比特位看是否为1。
//判断位图中是否全部位都被设置
bool all()
{
//前N个数
for (int i = 0; i < N / 32 ; i++)
{
int num = ~_bits[i];
if (num != 0)
{
return false;
}
}
//第N+1个数
for (size_t j = 0; j < N % 32; j++)
{
if ((_bits[N/32 - 1] & (1 << j)) == 0)
return false;
}
return true;
}
5. 经典面试题
5.1 问题一
给定
100亿个整数,设计算法找到只出现一次的整数?
首先数据量达到100亿,肯定使用位图,然后我们分析可以将每个整数分为三种状态:没有出现过,出现过一次,出现两次及其上。这时我们不可能用一个位图解决,因为一个位图只能表示两个状态,所以我们可以用两个位图来表示。其中00表示没有出现过,01表示只出现过一次,10表示出现过两次及其以上:
template<size_t N>
class bitTwo
{
public:
void set(size_t x)
{
//00->01
if (!_bit1.test(x) && !_bit2.test(x))
{
_bit2.set(x);
}
//01->10
else if(!_bit1.test(x) && _bit2.test(x))
{
_bit1.set(x);
_bit2.reset(x);
}
}
void PrintOnce()
{
for (int i = 0; i < N; i++)
{
//01
if (_bit2.test(i) == true)
{
cout << i << " ";
}
}
cout << endl;
}
private:
bitset<N> _bit1;
bitset<N> _bit2;
};
5.2 问题二
给两个文件,分别有
100亿个整数,我们只有1G内存,如何找到两个文件的交集?
我们提出以下两种解决方法:
方案一:
- 首先,依次读取第一个文件中的所有整数,将其映射到一个位图。这个位图需要有 2 32 2^{32} 232个比特位,即
512MB内存。- 然后,读取第二个文件中的所有整数,逐个判断其是否在位图中。如果在,则说明该整数是两个文件的交集之一;如果不在,则不是交集。
方案二:
- 第一步,依次读取第一个文件中的所有整数,将其映射到位图 1。同样,位图 1 有 2 32 2^{32} 232个比特位,占用
512M内存。- 第二步,依次读取第二个文件中的所有整数,将其映射到位图 2。位图 2 也占用
512M内存,两个位图刚好满足1G内存的限制。- 第三步,将位图 1 和位图 2 进行与操作,结果存储在位图 1 中。此时,位图 1 当中映射的整数就是两个文件的交集。
6. 位图源码
#include<vector>
#include<assert.h>
namespace betty
{
template<size_t N>
class bitset
{
public:
//构造函数
bitset()
{
_bits.resize(N / 32 + 1, 0);
}
//设置位
void set(size_t pos)
{
assert(pos < N);
int i = pos / 32;//第几个整型
int j = pos % 32;//第几个比特位
_bits[i] |= (1 << j);
}
//清空位
void reset(size_t pos)
{
assert(pos < N);
int i = pos / 32;//第几个整型
int j = pos % 32;//第几个比特位
_bits[i] &= ~(1<< j);
}
//反转位
void flip(size_t pos)
{
assert(pos < N);
int i = pos / 32;//第几个整型
int j = pos % 32;//第几个比特位
_bits[i] ^= (1 << j);
}
//获取位的状态
bool test(size_t pos)
{
assert(pos < N);
int i = pos / 32;//第几个整型
int j = pos % 32;//第几个比特位
if (_bits[i] & (1 << j))
{
return true;
}
return false;
}
//获取可以容纳的位的个数
size_t size()
{
return N;
}
//获取被设置位的个数
size_t count()
{
size_t cnt = 0;
for (int i = 0; i < N / 32 + 1; i++)
{
int num = _bits[i];
while (num)
{
num = num & (num - 1);
++cnt;
}
}
return cnt;
}
//判断位图中是否有位被设置
bool any()
{
for (int i = 0; i < N / 32 + 1; i++)
{
int num = _bits[i];
if (num != 0)
{
return true;
}
}
return false;
}
//判断位图中是否全部位都没有被设置
bool none()
{
return !any();
}
//判断位图中是否全部位都被设置
bool all()
{
for (int i = 0; i < N / 32 ; i++)
{
int num = ~_bits[i];
if (num != 0)
{
return false;
}
}
for (size_t j = 0; j < N % 32; j++)
{
if ((_bits[N/32 - 1] & (1 << j)) == 0)
return false;
}
return true;
}
private:
vector<int> _bits; //位图
};
}









![NSSCTF练习记录:[AFCTF 2018]BASE](https://i-blog.csdnimg.cn/direct/6a3d4a9e0d5d418f883b46319e839f0f.png)







