语言模型( language model) 用于计算一个文字序列的概率, 评估该序列作为一段文本出现在通用或者特定场景中的可能性。每个人的语言能力蕴涵了一个语言模型,当我们说出或写下一段话的时候,已经在不自觉地应用语言模型来帮助我们决定这段话中的每个词,使之通顺合理。语言模型在自然语言处理中也有诸多应用, 例如, 当我们使用拼音中文输入法输入“ ziranyuyan”, 输出的候选文字中“自然语言”比“孜然鱼雁”更靠前,这是因为中文输入法所使用的语言模型判断出前者的概率更高。类似地,在机器翻译、拼写检查、语音识别等应用中,语言模型也被用来在多项候选文字中选择更合理、更有可能出现的文字。
本节将首先概述语言模型,然后介绍不同的方法来实现语言模型, 包括最简单的n元语法模型、更复杂但效果更好的循环神经网络、在循环神经网络的基础上引入的注意力机制,以及纯粹基于注意力机制的 Transformer模型。
1. 概述
要想得到一个语言模型,最简单的想法是从一个大型语料库中直接统计不同文字序列出现的频率。然而由于文字序列的排列组合空间极大,不可能找到一个包含所有合理的文字序列的语料库,因此这个想法是不可行的。既然序列的概率无法通过经验频率来估计, 那么是否可以通过概率乘法公式将其转换为一系列条件概率的乘积,转而估算这些条件概率呢?
其中, 表示输入文字序列中的第i个词。那么这个序列“自然语言”的概率可以分解为
P(自然语言)=P(自)×P(然|自)×P(语|自然)×P(言|自然语)
这种分解方式的一个潜在好处在于,一旦能够成功估算所有可能的条件概率, 就可以用它们来生成文本。具体而言,首先根据第一个词的概率分布采样出第一个词,再根据给定第一个词时第二个词的条件概率分布采样出第二个词,然后根据给定前两个词时第三个词的条件概率分布采样出第三个词,以此类推。这种逐个词依次输出,每一步根据已输出的词决定下一个词的过程称为自回归 ( auto- regressive) 过程。
那么如何估算这些条件概率呢? 最直接的想法是最大似然估计:
P(言|自然语) = count(自然语言)/ count(自然语)
但这显然也是不可行的,同样因为我们无法找到一个足够大的包含所有合理文字序列的语料库来估算频率。因此,人们发展出了n元语法模型、循环神经网络、 Transformer模型等一系列方法来计算这些条件概率。
(1) n元语法(n- gram)模型: 每个词的概率仅以前n-1个词为条件。
(2) 循环神经网络( recurrent neural network, RNN): 每个词的概率以一个包含前置序列全部信息的稠密向量为条件。
(3) Transformer模型: 每个词的概率通过对前置所有词使用注意力机制得到。
本节将对这些方法的细节进行详细介绍。除了这些方法,还存在一些更加复杂的方法,如基于句法结构的生成式文法等,后面会介绍其中一些方法,这里不再展开。
所有这些方法所共同面临的一个问题是,如何处理在模型训练时没有见过的词,即所谓未登录( out- of- vocabulary, OOV) 词。一个常用方法是引入一个特殊词“[UNK]”: 在训练时,创建一个固定的词表(如所有高频词),将训练语料库中所有未在词表中出现的词都替换为“[UNK]”, 并将“[UNK]”作为一个正常词估算概率; 在测试时, 使用“[UNK]”的概率来代替任何未登录词的概率。除这个方法之外,还可以在字符或者子词级建立语言模型。因为任何词都可以拆解为若干字符或子词的组合,而字符或子词的个数较少,所以这样的语言模型能够涵盖所有字符或子词,从而涵盖所有可能的文字序列。
下面最后讨论如何评估一个语言模型的质量。一种方式是在下游任务(如机器翻译、语音识别等) 中检验语言模型的性能,但这往往比较费时费力, 并且不同下游任务的评估结果有可能大相径庭。因此,评估语言模型的通用方法是使用困惑度( perplexity), 即评估模型是否给训练语料库之外的真实测试语言语料库赋予较大的概率。对于测试语料库 (m个序列),使用待评估模型计算每个词的平均负对数概率:
其中, M为测试语料库中的总词数。该评价指标相当于编码每个词平均所需的比特数,其二次幂2'就被称为测试数据的困惑度。困惑度越小则测试语料库的概率越大,因此可认为被评估模型的质量越高。困惑度的最小值是1,这仅当所有测试语料的概率均为1的极端情况下才能取得。需要特别注意的是,词表不同的两个语言模型,其困惑度是不可比较的,显然,词表较小的语言模型平均会给每个词更高的概率,因而更有可能具有较低的困惑度,极端情况下,如果词表只包含“[UNK]”这一个词, 那么模型的困惑度可以达到完美的1。但词表过小的语言模型会将过多的词当作“[UNK]”,缺乏区分度,因而不是一个好的语言模型。因此,要比较不同的语言模型方法时, 需要使用统一的词表。
2. n元语法模型
在基础篇我们曾经谈论过n元语法模型,这里我们更深入讲解一番。下面是上文提到原处。
NLP从零开始------4基础文本处理之分词(1)_nlp 分词 词性标注-CSDN博客
在上面,我们使用概率乘法公式分解文字序列的概率, 但无法对分解得到的条件概率进行估算。为了估算这些条件概率,可以引入马尔可夫假设,即假设每个词只依赖它前面的n-1个词。
上述方法被称为n元语法模型。所谓n元语法是指文本中的连续n个词。最简单的情况为一元语法 ( unigram) 模型:
一元语法模型假设每个词出现的概率独立于其他词,这类似于 4.2.1节中朴素贝叶斯模型所做的假设。二元语法( bigram)模型则假设每个词只与上一个词有关,而和其他词无关:
类似地,可以定义三元语法模型、四元语法模型等。由于n元语法模型对于条件概率的限制条件是只包含n-1个词的序列,因此当n较小时,可能的条件序列也相对较少,可以从语料库中通过统计频率来估算。
n元语法模型的一个缺点在于无法建模所谓的长距离依赖(即距离大于n的两个词之间的依赖关系)。长距离依赖在自然语言中很常见,例如英语中动词所采用的单复数形式取决于主语,但动词与其主语之间可能间隔任意多个词(如对于一个很长的定语从句)。n元语法模型的另一个缺点是需要存储大量的条件概率,当n较大时模型会非常巨大。尽管有这些缺点, n元语法模型仍有很不错的性能,在神经网络语言模型出现之前是最为成功的语言模型。
接下来讨论如何从语料库中估算n元语法模型的条件概率。最简单的方式是最大似然估计:
但这样做的一个常见问题是数据稀疏性问题: 尽管限制了序列的长度,但是不同的n元语法仍然是非常多的,因此一些合理的n元语法可能不会在训练语料库中出现,从而导致相应的条件概率估算为0。这样一来,模型会将包含这些n元语法的文本的概率计算为0,这是不合理的。
常见的处理数据稀疏性问题的方法有以下几类:平滑法(拉普拉斯平滑)、回退法(找不到对应的n元语法时使用n-1元语法,仍找不到时使用n-2元语法, 以此类推)、插值法(将n元语法模型、n-1元语法模型、n-2元语法模型等一系列模型加权平均)。其中最为成功的方法是改良型 Kneser- Ney 平滑。
一个著名的n元语法数据集和可视化界面是 Google Ngram Viewer, 包含几百年来多种语言的公开文献中n元语法的出现频率统计, 可以查询其官网了解详细信息。
3. 循环神经网络(RNN)
基于神经网络的语言模型可以避免n元语法模型的各种缺点。神经网络语言模型中最基础的模型之一是循环神经网络( recurrent neural network, RNN), 它使用隐状态 ( hidden state)来保存历史信息,并使用循环结构逐一处理输入序列中的每一个元素。接下来首先介绍最基本的循环神经网络语言模型,然后介绍循环神经网络的两个著名变体——长短期记忆( long short- term memory, LSTM)和门控循环单元( gated recurrent unit, GRU)(门控循环单元可以看作长短期记忆的一种简化变体), 最后介绍多层双向循环神经网络。
3.1 循环神经网络
循环神经网络的基本思想是在计算文字序列中每个词的条件概率时,计算一个稠密向量来表示条件(也就是这个词的前置序列)所包含的信息,然后用该向量来计算条件概率分布。循环神经网络的架构如下图所示。

用于语言模型的循环神经网络
在这个模型结构中,每一步网络的输入包含两部分,一部分是历史输入,是前置序列的总结, 称为隐状态,另一部分是新的输入
,此处为词
所对应的词嵌入, 模型的输出经过 softmax函数处理得到下一步的词的分布,例如“自然语言”的下一个词可能是“处(理)”“生(成)”等。计算公式如下。
隐状态:
h⁽ᵗ⁾=σ(Wₓx⁽ᵗ⁾+Wₕh⁽ᵗ⁻¹⁾+bₕ)
输出:
其中,Wx为输入的参数,、
为隐藏层的参数,
、
为输出的参数,σ()在此处表示激活函数。初始隐状态
在没有其他信息的情况下一般设为全0。
循环神经网络的显著好处在于,解除了n元语法模型中对条件序列长度的限制,即不再使用马尔可夫假设,因而每一时刻的输出(即条件概率分布)都基于整个前置序列作为条件。并且,由于不需要像n元语法模型那样存储大量的条件概率,循环神经网络往往比典型的n元语法模型小, 即具有更少的模型参数。
下面讨论循环神经网络的训练。在每一步t, 训练损失函数为下一个词的预测分布与真实分布
(即下一个词
的独热编码) 的交叉熵( cross entropy):
其中, θ为模型参数,H(P,Q)=-∑ₓP(x)logQ(x)为两个概率分布P、Q的交叉熵, V为词表。注意, 真实分布只有在词
上概率为1, 在其余词上的概率为0, 因此可以去除求和符号而仅保留非零项, 即预测分布在词
上的概率。
总损失函数即为每一步交叉熵的平均值:
其中, T为总词数。该损失函数可以使用随机梯度下降进行优化。
下面用代码实现循环神经网络。首先读取数据,使用《小王子》这本书作为训练语料库。
import os
import sys
# 导入前面实现的小王子数据集
sys.path.append('./code')
from utils import TheLittlePrinceDataset
dataset = TheLittlePrinceDataset()
# 统计每句话的长度
sent_lens = []
max_len = -1
for sentence in dataset.tokens:
sent_len = len(sentence)
sent_lens.append(sent_len)
if sent_len > max_len:
max_len = sent_len
longest = sentence
print(max_len)
# 简单看一下语料中序列长度的分布
import matplotlib.pyplot as plt
plt.hist(sent_lens, bins=20)
plt.show()
然后建立词表,截断过长的序列, 将序列填充( padding) 为相同长度。实践中容易遇到极长的句子,这样的句子数量稀少但可能包含大量字符,如果不截断的话会极大拖慢模型的运行效率、占用大量显存甚至导致运行出错。因此在预处理阶段,可以对训练数据中过长的句子进行截断,即把预先确定的最大长度之外的词删去。注意, 一般不对测试数据进行截断,以便更完整地评估模型,并确保与其他工作的评估结果可比。为了使模型能够并行处理一个批次中不同长度的输入序列,可以使用填充将不同长度的输入对齐,常见做法是在长度不足的序列末尾持续添加特殊字符(如“[PAD]”)直到序列达到设定长度。填充可以在预处理阶段进行,这样会把所有输入序列填充为相同长度,也可以在训练过程中进行, 根据每个批次的序列长度动态设置填充长度。预处理阶段进行填充的好处是只需处理一次数据,并且处理完成的数据可以保存下来多次使用。训练过程中进行填充的好处是插入的特殊字符更少,减少了计算量。
import numpy as np
dataset.build_vocab()
sent_tokens = dataset.convert_tokens_to_ids()
# 截断和填充
max_len=40
for i, tokens in enumerate(sent_tokens):
tokens = tokens[:max_len]
tokens += [dataset.token2id['<pad>']] * (max_len - len(tokens))
sent_tokens[i] = tokens
sent_tokens = np.array(sent_tokens)
print(len(dataset.tokens), max([len(x) for x in dataset.tokens]))
print(sent_tokens.shape)
print(sent_tokens[0])1105 115
(1104, 40)
[ 4 17 20 742 743 744 742 743 744 2 62 19 9 1 1 2 1 10
745 746 4 17 20 21 1 2 30 335 194 33 299 3 0 0 0 0
0 0 0 0]import torch
from torch import nn
import torch.nn.functional as F
# 定义一个正态分布的函数用于初始化参数
def normal(shape):
return torch.randn(size=shape) * 0.01
class RNN(nn.Module):
def __init__(self, input_size, hidden_size):
super(RNN, self).__init__()
self.input_size = input_size
self.hidden_size = hidden_size
# 将输入与隐状态分别经过线性变化后相加
self.W_xh = nn.Parameter(normal((input_size, hidden_size)))
self.W_hh = nn.Parameter(normal((hidden_size, hidden_size)))
self.b_h = nn.Parameter(torch.zeros(hidden_size))
def init_rnn_state(self, batch_size, hidden_size):
return (torch.zeros((batch_size, hidden_size), dtype=torch.float),)
def forward(self, inputs, states):
seq_len, batch_size, _ = inputs.shape
hidden_state, = states
hiddens = []
for step in range(seq_len):
# 输入hidden_state与inputs经过线性变换后相加,
# 输出的hidden_state也是下一时刻输入的hidden_state
xh = torch.mm(inputs[step], self.W_xh)
hh = torch.mm(hidden_state, self.W_hh)
hidden_state = xh + hh + self.b_h
hidden_state = torch.tanh(hidden_state)
hiddens.append(hidden_state)
# 返回所有时刻的hidden_state: seq_len * batch_size * hidden_size
# 以及最后时刻的hidden_state(可能用于后续输入):
# batch_size * hidden_size
return torch.stack(hiddens, dim=0), (hidden_state,)
# 在循环神经网络的基础上添加语言模型的输入输出、损失计算等
class RNNLM(nn.Module):
def __init__(self, model, vocab_size, hidden_size):
super(RNNLM, self).__init__()
self.vocab_size = vocab_size
self.hidden_size = hidden_size
self.embedding = nn.Embedding(vocab_size, hidden_size)
self.model = model
self.W_hq = nn.Parameter(normal((hidden_size, vocab_size)))
self.b_q = nn.Parameter(torch.zeros(vocab_size))
def forward(self, input_ids):
batch_size, seq_len = input_ids.shape
# input_ids形状为batch_size * seq_len,翻转为seq_len * batch_size,
# 将seq_len放在第一维方便计算
input_ids = torch.permute(input_ids, (1, 0))
# seq_len * batch_size * embed_size
embed = self.embedding(input_ids)
# batch_size * hidden_size
states = self.model.init_rnn_state(batch_size, self.hidden_size)
hiddens, _ = self.model(embed, states)
hiddens = torch.flatten(hiddens[:-1], start_dim=0, end_dim=1)
output_states = torch.mm(hiddens, self.W_hq) + self.b_q
labels = torch.flatten(input_ids[1:], start_dim=0, end_dim=1)
loss_fct = nn.CrossEntropyLoss(ignore_index=0)
loss = loss_fct(output_states, labels)
return loss 接下来讨论循环神经网络训练过程中经常出现的一个问题。假设第t步的损失为,隐状态为
。由于总损失函数是各时刻损失函数的平均值, 因此训练过程中涉及各时刻的损失函数对历史时刻的求导, 这里以
对
求导为例, 根据链式法则展开梯度:
可以看到此梯度中包含连乘项,即每一时刻隐状态对上一时刻隐状态梯度的乘积。
在某些条件下,连乘项中的大部分因子小于1, 这会导致梯度随t的增加呈指数级衰减,这就是循环神经网络训练中著名的梯度消失问题。由此带来的后果是,距离远的梯度信号比距离近的梯度信号小得非常多,所以模型的参数实际上只能根据近距离的损失函数进行优化,从而破坏了长距离依赖。
反过来,如果大部分连乘项大于1, 又会导致梯度随t的增加呈指数级增长, 这就是循环神经网络训练中的梯度爆炸问题。梯度爆炸会导致参数更新幅度过大,从而可能使训练过程不稳定或是使参数落入损失函数很大的区域, 甚至导致 inf或NaN。
事实上, 梯度消失或梯度爆炸是神经网络训练中普遍存在的问题。对于循环神经网络,当输入序列较长时, 更容易发生梯度消失或梯度爆炸的问题。
对于梯度爆炸,一个非常直接的解决方案是梯度裁剪( gradient clipping), 即当梯度的模( norm) 超过某个阈值的时候,手动将其缩小到合理的范围内再使用梯度下降。那么, 梯度裁剪的思想是否也可以用于解决梯度消失问题,即当梯度的模低于某个阈值时手动将其增加到合理的范围呢?答案是否定的。这是因为当梯度的模较低时, 我们并不能确定是发生了梯度消失还是到达了损失函数的局部最优点,如果是后者, 那么增加梯度是不合理的, 这会导致梯度下降无法收敛。
下面展示使用梯度裁剪的循环神经网络语言模型的训练代码。
# 梯度裁剪
def grad_clipping(model, theta=1):
params = [p for p in model.parameters() if p.requires_grad]
norm = torch.sqrt(sum(torch.sum((p.grad ** 2)) for p in params))
if norm > theta:
for param in params:
param.grad[:] *= theta / norm
# 训练
from torch.utils.data import DataLoader
from torch.optim import SGD, Adam
import numpy as np
from tqdm import tqdm, trange
import matplotlib.pyplot as plt
def train_rnn_lm(data_loader, rnn, vocab_size, hidden_size=128,
epochs=200, learning_rate=1e-3):
# 准备模型、优化器等
rnn_lm = RNNLM(rnn, vocab_size, hidden_size)
optimizer = Adam(rnn_lm.parameters(), lr=learning_rate)
rnn_lm.zero_grad()
rnn_lm.train()
epoch_loss = []
with trange(epochs, desc='epoch', ncols=60) as pbar:
for epoch in pbar:
for step, batch in enumerate(data_loader):
loss = rnn_lm(batch)
pbar.set_description(f'epoch-{epoch}, ' + \
f'loss={loss.item():.4f}')
loss.backward()
grad_clipping(rnn_lm)
optimizer.step()
rnn_lm.zero_grad()
epoch_loss.append(loss.item())
epoch_loss = np.array(epoch_loss)
# 打印损失曲线
plt.plot(range(len(epoch_loss)), epoch_loss)
plt.xlabel('training epoch')
plt.ylabel('loss')
plt.show()
sent_tokens = np.array(sent_tokens)
print(sent_tokens.shape)
vocab_size = len(dataset.token2id)
data_loader = DataLoader(torch.tensor(sent_tokens, dtype=torch.long),\
batch_size=16, shuffle=True)
rnn = RNN(128, 128)
train_rnn_lm(data_loader, rnn, vocab_size, hidden_size=128,\
epochs=200, learning_rate=1e-3)(1104, 40)
epoch-199, loss=0.3491: 100%|█| 200/200 [04:42<00:00, 1.41s
3.2 长短期记忆
梯度消失问题的一个解决方案是使用循环神经网络的变体——长短期记忆( long short- term memory, LSTM)。
长短期记忆的原理是, 在每一步t, 都保存一个隐状态和一个单元状态( cell state)
, 通过单元状态来存储长距离信息, 长短期记忆模型使用3个门控( gate) 来控制单元状态的读写和擦除。这些门控同样以向量形式表示, 其中元素的取值为0或1,0表示门控关闭, 1表示门控打开。门控是动态变化的, 每一步都将重新计算门控。
接下来展示长短期记忆模型每一步的具体计算过程。假设第t步的输入为,隐状态与单元状态分别为
和
。我们依次计算如下向量, 所有向量的维度相同。
遗忘门( forget gate),控制上一个单元状态中的哪些信息被保留, 哪些信息被遗忘:
输入门( input gate), 控制哪些信息被写入单元状态:
i⁽ᵗ⁾=σ(Wᵢh⁽ᵗ⁻¹⁾+Uᵢx⁽ᵗ⁾+bᵢ)
输出门( output gate), 控制单元状态中的哪些信息被写入隐状态:
o⁽ᵗ⁾=σ(Wₒh⁽ᵗ⁻¹⁾+Uₒx⁽ᵗ⁾+bₒ)
新的单元内容, 即待写入单元的新信息:
单元状态,通过擦除(遗忘)上一个单元状态中的部分信息并写入部分新的信息而获得:
隐状态, 其内容是从单元状态中输出的一部分信息:
h⁽ᵗ⁾=o⁽ᵗ⁾tanhc⁽ᵗ⁾
其中,为 sigmoid 激活函数,
为 tanh 激活函数,⊙运算为逐元素相乘( element- wise product)。
长短期记忆的模型结构使得跨越多步保存信息变得更为简单直接: 如果某一维度的遗忘门打开、输入门关闭,那么单元状态中对应维度的信息就会被完全保存下来。通过这种方式可以跨越多步保留信息,从而更好地建模长距离依赖。而这种跨越多步的状态之间的依赖关系也意味着它们之间存在非零梯度,因而缓解了梯度消失问题。然而,长短期记忆并不能使所有门控会如我们所愿那样打开和关闭,因此不能保证完全没有梯度消失或梯度爆炸的问题,只是长短期记忆在大部分场景中缓解了这些问题。
接下来仿照循环神经网络实现长短期记忆,由于采用同样的接口, 我们可以复用之前的训练代码。
# 长短期记忆
def gate_params(input_size, hidden_size):
return (nn.Parameter(normal((input_size, hidden_size))),
nn.Parameter(normal((hidden_size, hidden_size))),
nn.Parameter(torch.zeros(hidden_size)))
class LSTM(nn.Module):
def __init__(self, input_size, hidden_size):
super(LSTM, self).__init__()
self.input_size = input_size
self.hidden_size = hidden_size
# 输入门参数
self.W_xi, self.W_hi, self.b_i = gate_params(input_size, hidden_size)
# 遗忘门参数
self.W_xf, self.W_hf, self.b_f = gate_params(input_size, hidden_size)
# 输出门参数
self.W_xo, self.W_ho, self.b_o = gate_params(input_size, hidden_size)
# 候选记忆单元参数
self.W_xc, self.W_hc, self.b_c = gate_params(input_size, hidden_size)
def init_rnn_state(self, batch_size, hidden_size):
return (torch.zeros((batch_size, hidden_size), dtype=torch.float),
torch.zeros((batch_size, hidden_size), dtype=torch.float))
def forward(self, inputs, states):
seq_len, batch_size, _ = inputs.shape
hidden_state, cell_state = states
hiddens = []
for step in range(seq_len):
I = torch.sigmoid(torch.mm(inputs[step], self.W_xi) \
+ torch.mm(hidden_state, self.W_hi) + self.b_i)
F = torch.sigmoid(torch.mm(inputs[step], self.W_xf) \
+ torch.mm(hidden_state, self.W_hf) + self.b_f)
O = torch.sigmoid(torch.mm(inputs[step], self.W_xo) \
+ torch.mm(hidden_state, self.W_ho) + self.b_o)
C_tilda = torch.tanh(torch.mm(inputs[step], self.W_xc) \
+ torch.mm(hidden_state, self.W_hc) + self.b_c)
cell_state = F * cell_state + I * C_tilda
hidden_state = O * torch.tanh(cell_state)
hiddens.append(hidden_state)
return torch.stack(hiddens, dim=0), (hidden_state, cell_state)
data_loader = DataLoader(torch.tensor(sent_tokens, dtype=torch.long),
batch_size=16, shuffle=True)
lstm = LSTM(128, 128)
train_rnn_lm(data_loader, lstm, vocab_size, hidden_size=128, epochs=200,
learning_rate=1e-3)代码结果:
epoch-199, loss=0.4065: 100%|█| 200/200 [29:26<00:00, 8.83s
长短期记忆有很多变体,其中一个著名的简化变体是门控循环单元( gated recurrent unit,GRU)。门控循环单元不再包含单元状态,门控也从3个减少到两个。我们同样给出第t步的计算过程, 其中输入为, 隐状态为
。
更新门( update gate), 控制隐状态中哪些信息被更新或者保留:
重置门( reset gate), 控制前一个隐状态中哪些部分被用来计算新的隐状态:
r⁽ᵗ⁾=σ(Wᵣh⁽ᵗ⁻¹⁾+Uᵣx⁽ᵗ⁾+bᵣ)
新的隐状态内容, 根据重置门从前一个隐状态中选择部分信息和当前的输入来计算:
隐状态,由更新门控制哪些部分来源于前一步的隐状态、哪些部分使用新计算的内容:
h⁽ᵗ⁾=(1-u⁽ᵗ⁾)⊙h⁽ᵗ⁻¹⁾+u⁽ᵗ⁾⊙h⁽ᵗ⁾
下面仿照长短期记忆实现门控循环单元。
# 门控循环单元
class GRU(nn.Module):
def __init__(self, input_size, hidden_size):
super(GRU, self).__init__()
self.input_size = input_size
self.hidden_size = hidden_size
# 更新门参数
self.W_xu, self.W_hu, self.b_u = gate_params(input_size, hidden_size)
# 重置门参数
self.W_xr, self.W_hr, self.b_r = gate_params(input_size, hidden_size)
# 候选隐状态参数
self.W_xh, self.W_hh, self.b_h = gate_params(input_size, hidden_size)
def init_rnn_state(self, batch_size, hidden_size):
return (torch.zeros((batch_size, hidden_size), dtype=torch.float),)
def forward(self, inputs, states):
seq_len, batch_size, _ = inputs.shape
hidden_state, = states
hiddens = []
for step in range(seq_len):
U = torch.sigmoid(torch.mm(inputs[step], self.W_xu)\
+ torch.mm(hidden_state, self.W_hu) + self.b_u)
R = torch.sigmoid(torch.mm(inputs[step], self.W_xr)\
+ torch.mm(hidden_state, self.W_hr) + self.b_r)
H_tilda = torch.tanh(torch.mm(inputs[step], self.W_xh)\
+ torch.mm(R * hidden_state, self.W_hh) + self.b_h)
hidden_state = U * hidden_state + (1 - U) * H_tilda
hiddens.append(hidden_state)
return torch.stack(hiddens, dim=0), (hidden_state,)
data_loader = DataLoader(torch.tensor(sent_tokens, dtype=torch.long),
batch_size=16, shuffle=True)
gru = GRU(128, 128)
train_rnn_lm(data_loader, gru, vocab_size, hidden_size=128, epochs=200,
learning_rate=1e-3)
#%% md
epoch-199, loss=0.2357: 100%|█| 200/200 [38:39<00:00, 11.60s
<Figure size 640x480 with 1 Axes>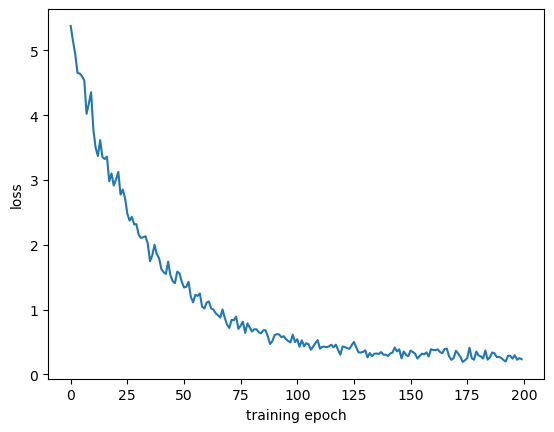
3.3 多层双向循环神经网络
循环神经网络(包括像长短期记忆这样的变体) 可以很方便地扩展为多层和双向结构。
多层循环神经网络将多个循环神经网络堆叠起来,前一层的输出作为后一层的输入, 最后一层的输出作为整个模型最终的输出。通过这种方式可以增加整个模型的表达能力,以获得更好的效果, 如图所示。

下面在循环神经网络的基础上实现多次循环神经网络。
# 多层循环神经网络
class DeepRNN(nn.Module):
def __init__(self, input_size, hidden_size, num_layers, dropout=0.):
super(DeepRNN, self).__init__()
self.input_size = input_size
self.hidden_size = hidden_size
self.num_layers = num_layers
self._flat_weight_names = []
self._all_weights = []
self.drop = nn.Dropout(p=dropout)
# 定义每一层循环神经网络的参数,由于参数数量不固定,
# 因此使用统一的命名方法更方便调用和管理
for layer in range(num_layers):
W_xh = nn.Parameter(normal((input_size, hidden_size)))
W_hh = nn.Parameter(normal((hidden_size, hidden_size)))
b_h = nn.Parameter(torch.zeros(hidden_size))
layer_params = (W_xh, W_hh, b_h)
params_names = [f'W_xh_l{layer}', f'W_hh_l{layer}', \
f'b_h_l{layer}']
# 将新的参数加入到成员列表中
for name, param in zip(params_names, layer_params):
setattr(self, name, param)
self._flat_weight_names.extend(params_names)
self._all_weights.append(params_names)
input_size = hidden_size
self._flat_weights = [getattr(self, wn) if hasattr(self, wn) \
else None for wn in self._flat_weight_names]
def __setattr__(self, attr, value):
if hasattr(self, '_flat_weight_names') and \
attr in self._flat_weight_names:
idx = self._flat_weight_names.index(attr)
self._flat_weights[idx] = value
super().__setattr__(attr, value)
def init_rnn_state(self, batch_size, hidden_size):
return (torch.zeros((self.num_layers, batch_size, hidden_size),
dtype=torch.float),)
def forward(self, inputs, states):
seq_len, batch_size, _ = inputs.shape
layer_hidden_states, = states
layer_h_t = []
input_states = inputs
# 需要保存每一层的输出作为下一层的输入
for layer in range(self.num_layers):
hiddens = []
hidden_state = layer_hidden_states[layer]
for step in range(seq_len):
xh = torch.mm(input_states[step],
getattr(self, f'W_xh_l{layer}'))
hh = torch.mm(hidden_state, getattr(self, f'W_hh_l{layer}'))
hidden_state = xh + hh + getattr(self, f'b_h_l{layer}')
hidden_state = self.drop(torch.tanh(hidden_state))
hiddens.append(hidden_state)
input_states = torch.stack(hiddens, dim=0)
layer_h_t.append(hidden_state)
return input_states, torch.stack(layer_h_t, dim=0)
data_loader = DataLoader(torch.tensor(sent_tokens, dtype=torch.long),
batch_size=16, shuffle=True)
deep_rnn = DeepRNN(128, 128, 2)
train_rnn_lm(data_loader, deep_rnn, vocab_size, hidden_size=128,
epochs=200, learning_rate=1e-3)
epoch-199, loss=0.3928: 100%|█| 200/200 [34:04<00:00, 10.22s
<Figure size 640x480 with 1 Axes>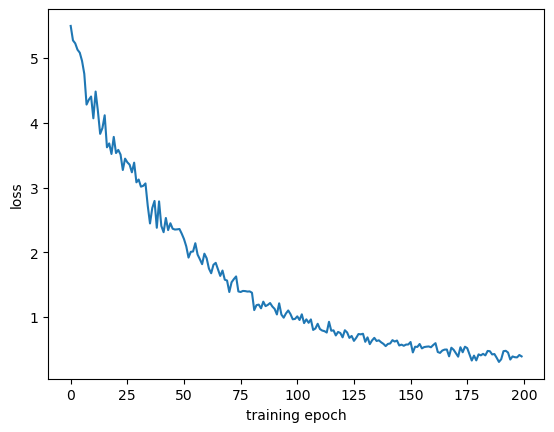
双向循环神经网络的结构包含一个正向的循环神经网络和一个反向的循环神经网络(即从右到左读入文字序列),将这两个网络对应位置的输出拼接得到最终的输出,如下图所示。

需要注意的是,双向循环神经网络在每个位置的输出同时包含来自左边和右边的信息,也就是整个输入序列的信息,因此双向循环神经网络不能用于语言模型,因为语言模型需要仅根据序列中每个词左边的信息来预测这个词。但是,在后续章节所讨论的很多其他任务中,双向循环神经网络因可以利用整个输入序列的信息而有着比单向循环神经网络更好的表现。
下面的双向循环神经网络是一个简单的示例,要求一次只能输入一个序列。如果想在一个批次中并行处理不同长度的输入序列以获得更高的运行效率,可以通过填充将不同长度的输入序列对齐。单向循环神经网络的填充较为简单,只需在每个序列末尾添加字符。双向循环神经网络的填充更加复杂,正向和反向的循环神经网络的读取顺序相反, 难以保证两个方向的循环神经网络都在末尾填充,实现起来较为困难。有关解决方案可以参考PyTorch中的 pack _ padded _ sequence 和 pad _ packed _ sequence。双向循环神经网络不能用于训练语言模型,因此不再提供训练示例代码。
# 双向循环神经网络
class BiRNN(nn.Module):
def __init__(self, input_size, hidden_size):
super(BiRNN, self).__init__()
self.input_size = input_size
self.hidden_size = hidden_size
# 正向循环神经网络参数
self.W_xh = nn.Parameter(normal((input_size, hidden_size)))
self.W_hh = nn.Parameter(normal((hidden_size, hidden_size)))
self.b_h = nn.Parameter(torch.zeros(hidden_size))
# 反向循环神经网络参数
self.W_xh_reverse = nn.Parameter(normal((input_size, hidden_size)))
self.W_hh_reverse = nn.Parameter(normal((hidden_size, hidden_size)))
self.b_h_reverse = nn.Parameter(torch.zeros(hidden_size))
# 分别为正向和反向循环神经网络准备初始状态
def init_rnn_state(self, batch_size, hidden_size):
return (torch.zeros((batch_size, hidden_size), dtype=torch.float),
torch.zeros((batch_size, hidden_size), dtype=torch.float))
def forward(self, inputs, states):
seq_len, batch_size, _ = inputs.shape
hidden_state, reverse_hidden_state = states
hiddens = []
for step in range(seq_len):
xh = torch.mm(inputs[step], self.W_xh)
hh = torch.mm(hidden_state, self.W_hh)
hidden_state = xh + hh + self.b_h
hidden_state = torch.tanh(hidden_state)
hiddens.append(hidden_state)
reverse_hiddens = []
for step in range(seq_len-1, -1, -1):
xh = torch.mm(inputs[step], self.W_xh_reverse)
hh = torch.mm(reverse_hidden_state, self.W_hh_reverse)
reverse_hidden_state = xh + hh + self.b_h_reverse
reverse_hidden_state = torch.tanh(reverse_hidden_state)
reverse_hiddens.insert(0, reverse_hidden_state)
# 将正向和反向循环神经网络输出的隐状态拼接在一起
combined_hiddens = []
for h1, h2 in zip(hiddens, reverse_hiddens):
combined_hiddens.append(torch.cat([h1, h2], dim=-1))
return torch.stack(combined_hiddens, dim=0), ()
4. 注意力机制
4.1 注意力机制
循环神经网络的一个主要局限是不能很好地建模长距离依赖,即使像长短期记忆这样的变体也只是改善而不是完全解决了长距离依赖的问题。其根本原因在于,如果序列中的第i个词需要对第j个词(假设j>i)产生影响,需经过j-i个计算步骤, 而随着步数增加, 第i个词的信息会很快衰减,被两个词之间其他词的信息所淹没。从另一个角度来看, 每一步用来预测下一个词的隐状态都需要包含这个词左边所有词的信息,但隐状态的维度有限,因而所能表达的信息容量也有限,从而形成了信息瓶颈, 阻碍了前置词信息的准确表示和传递。
为了更好地建模长距离依赖,我们引入注意力机制( attention mechanism)。在每一步,我们直接在历史状态和当前状态之间建立联系。由于历史状态可能很多,在重要性和相关性上会有区别,因此我们希望模型能够自动预测这种重要性和相关性,这类似于人类的注意力。
具体而言, 注意力机制根据当前状态计算查询( query), 根据每一个历史隐状态计算键( key), 进而计算查询与键的匹配程度,即注意力分数( attention score)。注意力分数越高,意味着对应的历史隐状态对当前时刻的预测越重要。对所有历史隐状态的注意力分数进行归一化, 我们就得到了对历史的注意力分布。接下来,以注意力分布的值作为权重,将所有历史隐状态所计算出的值( value) 向量进行加权平均,得到最终的注意力输出向量,用于代替当前状态向量来预测下一个词。
注意力分数有多种计算方式,下面给出的注意力机制的公式将查询和键的内积作为注意力分数, 即点乘注意力( dot- product attention)。假设某一组查询、键、值分别为q∈、
、
,其中查询和键的维度与值的维度可以是不同的,但是为了简单起见, 实现时可以令这些向量维度相等:
。
对于一个查询和整个序列的键、值来说,当前查询对应的注意力输出向量是:
其中, K和V分别是将整个序列的键向量和值向量堆叠而成的矩阵:。
为查询q在第i个位置的注意力分数,
为归一化项。
输入序列的每一步都需要进行上述注意力机制的计算。可以将输入序列所有位置上的注意力计算合并, 即将序列中所有步骤的查询堆叠为Q=[q_{1}, \cdots ,q_{n}],由此得到注意力计算的矩阵形式:
Attention(Q,K,V)= softmax(Q)V
需要注意的是,在前面的讲解中,一个查询会对整个序列的所有位置计算注意力,但是对于语言模型,第t步的查询应当只能看到该步及该步之前的输入。因此,需要引入注意力掩码( attention mask), 将每一步的查询对该步之后位置的注意力分数置为- inf。
这里所讲解的注意力机制,每一步的隐状态既用于计算当前步的查询, 又用于计算其他查询的键和值。也就是说,不考虑注意力掩码的话,我们是在输入序列的所有位置两两之间计算注意力, 即输入序列对于自身的注意力。
因此,这种特殊的注意力结构又称作自注意力( self attention)。区别于自注意力, 注意力机制本身更加通用,也适用于查询、键和值对应不同元素的场景.
基于点乘的注意力分数计算有一个潜在的问题,即随着查询和键的维度dₖ的增大,不同的键所计算的内积的数值范围也会逐渐增大,由此会带来 softmax函数的数值稳定性问题。为了解决这个问题,可以采用缩放点乘注意力( scaled dot- product attention), 即
下面实现一个带有缩放点乘注意力的循环神经网络,并用其训练语言模型。
class AttentionRNN(nn.Module):
def __init__(self, input_size, hidden_size):
super(AttentionRNN, self).__init__()
self.input_size = input_size
self.hidden_size = hidden_size
# 循环神经网络参数
self.W_xh = nn.Parameter(normal((input_size, hidden_size)))
self.W_hh = nn.Parameter(normal((hidden_size, hidden_size)))
self.b_h = nn.Parameter(torch.zeros(hidden_size))
def init_rnn_state(self, batch_size, hidden_size):
return (torch.zeros((batch_size, hidden_size),\
dtype=torch.float),)
# 缩放点乘注意力
def attention(self, query, keys, values):
"""
query: batch_size * hidden_size
keys/values: batch_size * prev_len * hidden_size
"""
# batch_size * 1 * hidden_size
query = torch.unsqueeze(query, 1)
# batch_size * hidden_size * prev_len
keys = torch.permute(keys, (0, 2, 1))
# batch_size * 1 * prev_len
attention_scores = torch.bmm(query, keys) / np.sqrt(\
self.hidden_size)
# batch_size * 1 * prev_len
attention_weights = F.softmax(attention_scores, dim=1)
# batch_size * hidden_size
attention_state = torch.squeeze(torch.bmm(attention_weights,\
values))
return attention_state
def forward(self, inputs, states):
seq_len, batch_size, _ = inputs.shape
hidden_state, = states
hiddens = []
attention_hiddens = []
for step in range(seq_len):
xh = torch.mm(inputs[step], self.W_xh)
hh = torch.mm(hidden_state, self.W_hh)
hidden_state = xh + hh + self.b_h
hidden_state = torch.tanh(hidden_state)
if step > 0:
# batch_size * hidden_size
query = hidden_state
# batch_size * prev_len * hidden_size
keys = values = torch.permute(torch.stack(hiddens,\
dim=0), (1, 0, 2))
attention_state = self.attention(query, keys, values)
attention_hiddens.append(attention_state)
else:
# 第0步,历史隐状态为空,无法进行注意力运算,
# 直接用隐状态填充
attention_hiddens.append(hidden_state)
hiddens.append(hidden_state)
return torch.stack(attention_hiddens, dim=0), \
(attention_state,)
data_loader = DataLoader(torch.tensor(sent_tokens, dtype=torch.long),
batch_size=16, shuffle=True)
attention_rnn = AttentionRNN(128, 128)
train_rnn_lm(data_loader, attention_rnn, vocab_size, hidden_size=128,
epochs=200, learning_rate=1e-3)
#%% md
epoch-199, loss=1.1505: 100%|█| 200/200 [17:54<00:00, 5.37s
值得一提的是,注意力机制在每一步都需要查看整个历史,所以当序列很长时,注意力机制的计算代价就会很高。这种情况下一般会设置一个固定大小的上下文窗口,将注意力局限于窗口之内。
4.2 多头注意力
普通的注意力只允许不同的词之间通过一种方式进行交互,这可能会限制模型的表达能力。一个改进方案是多头注意力( multi- head attention), 即允许词之间通过多种不同方式进行交互, 具体做法如下。
将Q、K、V映射到m个不同的低维空间中。对i=1,2,…,m, 分别计算:
在每个低维空间中独立使用注意力机制:
=Attention(Qᵢ,Kᵢ,Vᵢ)
将不同低维空间的注意力输出向量拼接起来做一个线性变换, 其中表示将不同头的注意力输出向量拼接起来:
下面是多头注意力的代码实现。我们在实现AttentionRNN类时将注意力计算封装在成员函数里面, 因此实现多头注意力时可以直接继承AttentionRNN 类, 只需改写构造函数和 attention() 成员方法。
# 多头注意力循环神经网络
class MultiHeadAttentionRNN(AttentionRNN):
def __init__(self, input_size, hidden_size, num_heads=4):
super().__init__(input_size, hidden_size)
# 简单起见,一般要求hidden_size能够被num_heads整除
assert hidden_size % num_heads == 0
self.num_heads = num_heads
# 多头注意力参数,用于将查询、键、值映射到子空间
self.W_aq = nn.Parameter(normal((hidden_size, hidden_size)))
self.b_aq = nn.Parameter(torch.zeros(hidden_size))
self.W_ak = nn.Parameter(normal((hidden_size, hidden_size)))
self.b_ak = nn.Parameter(torch.zeros(hidden_size))
self.W_av = nn.Parameter(normal((hidden_size, hidden_size)))
self.b_av = nn.Parameter(torch.zeros(hidden_size))
self.W_ac = nn.Parameter(normal((hidden_size, hidden_size)))
self.b_ac = nn.Parameter(torch.zeros(hidden_size))
# 多头缩放点乘注意力
def attention(self, query, keys, values):
"""
query: batch_size * hidden_size
keys/values: batch_size * prev_len * hidden_size
"""
query = torch.mm(query, self.W_aq) + self.b_aq
ori_shape = keys.size()
keys = torch.reshape(torch.mm(torch.flatten(keys,
start_dim=0, end_dim=1), self.W_ak) +
self.b_ak, ori_shape)
values = torch.reshape(torch.mm(torch.flatten(values,
start_dim=0, end_dim=1), self.W_av) +
self.b_av, ori_shape)
# batch_size * 1 * hidden_size
query = torch.unsqueeze(query, 1)
# batch_size * hidden_size * prev_len
keys = torch.permute(keys, (0, 2, 1))
head_size = self.hidden_size // self.num_heads
query = torch.split(query, head_size, 2)
keys = torch.split(keys, head_size, 1)
values = torch.split(values, head_size, 2)
heads = []
for i in range(self.num_heads):
# batch_size * 1 * prev_len
head_scores = torch.bmm(query[i], keys[i]) / np.sqrt(
self.hidden_size // self.num_heads)
# batch_size * 1 * prev_len
head_weights = F.softmax(head_scores, dim=1)
# batch_size * head_size
head_state = torch.squeeze(torch.bmm(head_weights,
values[i]))
heads.append(head_state)
heads = torch.cat(heads, dim=1)
attention_state = torch.mm(heads, self.W_ac) + self.b_ac
return attention_state
data_loader = DataLoader(torch.tensor(sent_tokens,
dtype=torch.long), batch_size=16, shuffle=True)
mha_rnn = MultiHeadAttentionRNN(128, 128)
train_rnn_lm(data_loader, mha_rnn, vocab_size, hidden_size=128,
epochs=200, learning_rate=1e-3)epoch-199, loss=1.3427: 100%|█| 200/200 [50:47<00:00, 15.24s
5.Transformer模型
上面在循环神经网络的基础上增加了注意力机制,循环神经网络基于循环连接来间接访问历史隐状态,而注意力机制能够直接访问历史隐状态。一个很自然的问题是, 能否去掉循环神经网络,只利用注意力机制来完成语言模型呢? 基于这样的想法, 我们就得到了 Transformer模型。
Transformer将循环神经网络中相邻隐状态之间的连接完全去除, 只保留注意力机制,因此不同位置的隐状态之间不存在计算上的依赖关系, 完全可以并行计算, 如下图所示。

并行计算是 Transformer相比于循环神经网络的一个显著优势。但是这样一来也引入了一个新的问题,即模型完全没有考虑词的顺序信息,而把输入文字序列看作词的集合,这对于建模自然语言而言显然是不妥的。为了解决这个问题,可以在模型中引入位置编码。一种做法是绝对位置编码,即给输入序列中的每个位置指定或者学习一个位置嵌入, 将其加到对应位置的词嵌入上作为模型的输入。另一种做法是相对位置编码,即在计算注意力时编码词之间的相对位置, 具体做法如下。首先计算相对位置索引:
rᵢⱼ=clip(i-j,-s,s)
其中, clip()是截断函数, s为预先设定的相对位置的截断上界。然后计算考虑了相对位置编码的注意力分数:
其中, 为与
维度相同的向量, 注意每个相对位置索引
都对应一个不同的向量
。最后在计算注意力输出向量时也加入另一组相对位置编码:
其中,类似于
,
为注意力分数
归一化后得到的权重。
仅使用注意力机制的另一个问题是,注意力输出只是对值向量进行了线性组合, 而以往的工作表明非线性变换可以增加模型的表达能力。因此,我们在注意力的输出上增加一个使用非线性激活函数的两层前馈神经网络( feed- forward neural network, FNN)。前馈神经网络有时也被称为多层感知机( multi- layer perceptron, MLP)。
其中,、
通常分别对其输入进行升维和降维操作(例如在经典的 Transformer 结构中, a=4b)。
Transformer模型会将上述注意力机制和前馈神经网络堆叠若干层,以增加模型的表达能力。这种方式类似于6.3.3节介绍的多层双向循环神经网络。为了增加这样的多层模型的训练稳定性, 降低训练难度, 我们进一步引入两个技巧。一是引入残差连接( residual connection).
xˡ=F(xˡ⁻¹)+xˡ⁻¹
其中,xˡ⁻¹为残差连接的输入,xˡ 为残差连接的输出, F()为一层注意力机制或前馈神经网络,二是层归一化 ( layer normalization) . 将每一层的输出归一化到均值为0、方差为1,再进行可学习的仿射变换:
其中,xˡ为层归一化的输入,μˡ与σ分别为输入.xˡ的均值和标准差,xˡ'是层归一化的输出, ∈是一个用于维持数值稳定性的很小的常数,gˡ和bˡ为可学习的仿射变换的参数。
如同上文所讨论的那样, 当 Transformer用于语言模型时, 还需要加上注意力掩码, 以保证每一步查询不会和该步之后的键、值做计算。最后,将模型顶层所输出的每个位置的隐状态输入一个线性分类器中, 得到下一个词的预测分布。整个 Transformer模型的架构如下图所示。

transformer结构图
下面来实现 Transformer模型, 包括加入了位置编码的嵌入层,缩放点注意力,多头注意意力、层归一化等具体实现。
# 实现Transformer模型
class EmbeddingLayer(nn.Module):
def __init__(self, vocab_size, max_len, embed_size):
super().__init__()
self.vocab_size = vocab_size
self.max_len = max_len
self.embed_size = embed_size
self.word_embedding = nn.Embedding(vocab_size, embed_size)
self.pos_embedding = nn.Embedding(max_len, embed_size)
def forward(self, input_ids, pos_ids):
"""
input_ids/pos_ids: batch_size * seq_len
return: batch_size * seq_len * embed_size
"""
word_embed = self.word_embedding(input_ids)
pos_embed = self.pos_embedding(pos_ids)
# 将词嵌入和位置嵌入相加得到嵌入层输出
return word_embed + pos_embed
# 缩放点乘注意力
class ScaledDotProductAttention(nn.Module):
def __init__(self, dropout):
super().__init__()
self.dropout = nn.Dropout(dropout)
def forward(self, queries, keys, values, attention_mask):
"""
queries/keys/values: batch_size * seq_len * hidden_size
attention_mask: batch_size * seq_len * seq_len
return: batch_size * seq_len * hidden_size
"""
d = queries.size(-1)
# 根据点乘注意力的矩阵形式计算注意力分数,除以查询向量或键向量
# 维度的平方根,即为缩放点乘注意力
scores = torch.bmm(queries, torch.transpose(keys, 1, 2)) / np.sqrt(d)
# 将掩码为0的位置的注意力分数设为一个大负数,根据softmax函数
# 的性质,这些注意力分数归一化后接近0
scores[attention_mask == 0] = -1e6
self.attention_weights = F.softmax(scores, dim=-1)
return torch.bmm(self.dropout(self.attention_weights), values)
class MultiHeadSelfAttention(nn.Module):
def __init__(self, hidden_size, num_heads, dropout):
super().__init__()
assert hidden_size % num_heads == 0
self.hidden_size = hidden_size
self.num_heads = num_heads
self.W_q = nn.Linear(hidden_size, hidden_size)
self.W_k = nn.Linear(hidden_size, hidden_size)
self.W_v = nn.Linear(hidden_size, hidden_size)
self.W_o = nn.Linear(hidden_size, hidden_size)
self.attention = ScaledDotProductAttention(dropout)
def transpose_qkv(self, states):
# 将长度为hidden_size的向量分成num_heads个长度相等的向量
states = states.reshape(states.shape[0], states.shape[1],\
self.num_heads, self.hidden_size // self.num_heads)
states = torch.permute(states, (0, 2, 1, 3))
return states.reshape(-1, states.shape[2], states.shape[3])
# 与transpose_qkv的变换相反
def transpose_output(self, states):
states = states.reshape(-1, self.num_heads, states.shape[1],\
states.shape[2])
states = torch.permute(states, (0, 2, 1, 3))
return states.reshape(states.shape[0], states.shape[1], -1)
def forward(self, queries, keys, values, attention_mask):
"""
querys/keys/values: batch * seq_len * hidden_size
attention_mask: batch * seq_len * seq_len
return:
"""
# (batch_size * num_heads) * seq_len * (hidden_size / num_heads)
queries = self.transpose_qkv(self.W_q(queries))
keys = self.transpose_qkv(self.W_k(keys))
values = self.transpose_qkv(self.W_v(values))
# 重复张量的元素,用以支持多个注意力头的运算
# (batch_size * num_heads) * seq_len * seq_len
attention_mask = torch.repeat_interleave(attention_mask,\
repeats=self.num_heads, dim=0)
# (batch_size * num_heads) * seq_len * (hidden_size / num_heads)
output = self.attention(queries, keys, values, attention_mask)
# batch * seq_len * hidden_size
output_concat = self.transpose_output(output)
return self.W_o(output_concat)
# 两层前馈神经网络
class PositionWiseFNN(nn.Module):
def __init__(self, hidden_size, intermediate_size):
super().__init__()
self.dense1 = nn.Linear(hidden_size, intermediate_size)
self.relu = nn.ReLU()
self.dense2 = nn.Linear(intermediate_size, hidden_size)
def forward(self, X):
return self.dense2(self.relu(self.dense1(X)))
# 层归一化
class LayerNorm(nn.Module):
def __init__(self, normalized_shape, eps=1e-6):
super().__init__()
self.gamma = nn.Parameter(torch.ones(normalized_shape))
self.beta = nn.Parameter(torch.zeros(normalized_shape))
# 一个小量用于数值稳定(防止除0)
self.eps = eps
def forward(self, hidden_states):
mean = torch.mean(hidden_states, -1, keepdim=True)
std = torch.std(hidden_states, -1, keepdim=True)
return self.gamma * (hidden_states - mean) / (std +\
self.eps) + self.beta
# 将两个输入相加并归一化
class AddNorm(nn.Module):
def __init__(self, hidden_size, dropout):
super().__init__()
self.dropout = nn.Dropout(dropout)
self.layer_norm = LayerNorm(hidden_size)
def forward(self, X, Y):
return self.layer_norm(self.dropout(Y) + X)
# 一个完整的Transformer层
class TransformerLayer(nn.Module):
def __init__(self, hidden_size, num_heads, dropout, intermediate_size):
super().__init__()
self.self_attention = MultiHeadSelfAttention(hidden_size,\
num_heads, dropout)
self.add_norm1 = AddNorm(hidden_size, dropout)
self.fnn = PositionWiseFNN(hidden_size, intermediate_size)
self.add_norm2 = AddNorm(hidden_size, dropout)
def forward(self, X, attention_mask):
Y = self.add_norm1(X, self.self_attention(X, X, X, attention_mask))
return self.add_norm2(Y, self.fnn(Y))# 在Transformer模型基础上加上语言模型需要的输入输出、损失计算等
class TransformerLM(nn.Module):
def __init__(self, vocab_size, max_len, hidden_size, num_layers,\
num_heads, dropout, intermediate_size):
super().__init__()
self.embedding_layer = EmbeddingLayer(vocab_size, max_len,\
hidden_size)
self.num_layers = num_layers
# 使用ModuleList保存多个Transformer层,注意不能使用Python列表,
# Python列表保存的PyTorch变量无法自动求导
self.layers = nn.ModuleList([TransformerLayer(hidden_size,\
num_heads, dropout, intermediate_size)\
for _ in range(num_layers)])
self.output_layer = nn.Linear(hidden_size, vocab_size)
def forward(self, input_ids):
# 这里实现的forward()函数一次只能处理一句话,
# 如果想要支持批次运算,实现起来会更复杂,也会引入冗余操作
seq_len = input_ids.size(0)
assert input_ids.ndim == 1 and seq_len <= \
self.embedding_layer.max_len
# 1 * seq_len
input_ids = torch.unsqueeze(input_ids, dim=0)
pos_ids = torch.unsqueeze(torch.arange(seq_len), dim=0)
# 定义下三角掩码,用于语言模型训练
# 1 * seq_len * seq_len
attention_mask = torch.unsqueeze(torch.tril(torch.ones((seq_len,\
seq_len), dtype=torch.int32)), dim=0)
# 1 * seq_len * hidden_size
hidden_states = self.embedding_layer(input_ids, pos_ids)
for layer in self.layers:
hidden_states = layer(hidden_states, attention_mask)
outputs = self.output_layer(hidden_states)
loss_fct = nn.CrossEntropyLoss(ignore_index=0)
loss = loss_fct(outputs[:, :-1].squeeze(),\
input_ids[:, 1:].squeeze())
return loss# 在Transformer模型基础上加上语言模型需要的输入输出、损失计算等
class TransformerLM(nn.Module):
def __init__(self, vocab_size, max_len, hidden_size, num_layers,\
num_heads, dropout, intermediate_size):
super().__init__()
self.embedding_layer = EmbeddingLayer(vocab_size, max_len,\
hidden_size)
self.num_layers = num_layers
# 使用ModuleList保存多个Transformer层,注意不能使用Python列表,
# Python列表保存的PyTorch变量无法自动求导
self.layers = nn.ModuleList([TransformerLayer(hidden_size,\
num_heads, dropout, intermediate_size)\
for _ in range(num_layers)])
self.output_layer = nn.Linear(hidden_size, vocab_size)
def forward(self, input_ids):
# 这里实现的forward()函数一次只能处理一句话,
# 如果想要支持批次运算,实现起来会更复杂,也会引入冗余操作
seq_len = input_ids.size(0)
assert input_ids.ndim == 1 and seq_len <= \
self.embedding_layer.max_len
# 1 * seq_len
input_ids = torch.unsqueeze(input_ids, dim=0)
pos_ids = torch.unsqueeze(torch.arange(seq_len), dim=0)
# 定义下三角掩码,用于语言模型训练
# 1 * seq_len * seq_len
attention_mask = torch.unsqueeze(torch.tril(torch.ones((seq_len,\
seq_len), dtype=torch.int32)), dim=0)
# 1 * seq_len * hidden_size
hidden_states = self.embedding_layer(input_ids, pos_ids)
for layer in self.layers:
hidden_states = layer(hidden_states, attention_mask)
outputs = self.output_layer(hidden_states)
loss_fct = nn.CrossEntropyLoss(ignore_index=0)
loss = loss_fct(outputs[:, :-1].squeeze(),\
input_ids[:, 1:].squeeze())
return loss
#%%
# 训练TransformerLM,由于不再采取批次训练,因此不再使用RNNLM和data_loader
def train_transformer_lm(data, model, epochs=50, learning_rate=1e-3):
optimizer = Adam(model.parameters(), lr=learning_rate)
model.zero_grad()
model.train()
epoch_loss = []
with trange(epochs, desc='epoch', ncols=60) as pbar:
for epoch in pbar:
step_loss = []
np.random.shuffle(data)
for step, x in enumerate(data):
loss = model(torch.tensor(x, dtype=torch.long))
pbar.set_description(f'epoch-{epoch},'+\
f' loss={loss.item():.4f}')
loss.backward()
grad_clipping(model)
optimizer.step()
model.zero_grad()
step_loss.append(loss.item())
# 本章前面的模型训练使用batch_size为16,
# TransformerLM出于简便实现只能使用batch_size为1
# 因此TransformerLM每一步的损失方差会更大,
# 为便于对比,取每个epoch最后16个样本的平均损失
epoch_loss.append(np.mean(step_loss[-16:]))
epoch_loss = np.array(epoch_loss)
plt.plot(range(len(epoch_loss)), epoch_loss)
plt.xlabel('training epoch')
plt.ylabel('loss')
plt.show()
sent_tokens = dataset.convert_tokens_to_ids()
max_len=40
for i, tokens in enumerate(sent_tokens):
tokens = tokens[:max_len]
tokens += [0] * (max_len - len(tokens))
sent_tokens[i] = tokens
sent_tokens = np.array(sent_tokens)
model = TransformerLM(vocab_size, max_len=40, hidden_size=128,\
num_layers=1, num_heads=4, dropout=0., intermediate_size=512)
train_transformer_lm(sent_tokens, model)epoch-49, loss=0.3176: 100%|█| 50/50 [13:47<00:00, 16.54s/it









![[Pyplot]设置图中字体为TimesNewRoman](https://i-blog.csdnimg.cn/direct/8ae309f853ca4771a6c40e25d0a551e3.png)








