Datawhale X 李宏毅苹果书 AI夏令营 task2

news2024/12/25 9:07:30

《深度学习详解》 - 自适应学习率（Task2）

1. 自适应学习率的背景与重要性

学习率的挑战：
在训练深度学习模型时，选择合适的学习率至关重要。过大的学习率会导致训练过程中的震荡，使模型无法收敛；过小的学习率则会导致训练速度缓慢，甚至可能陷入局部最优解。为了克服这些问题，自适应学习率（Adaptive Learning Rate）算法应运而生。

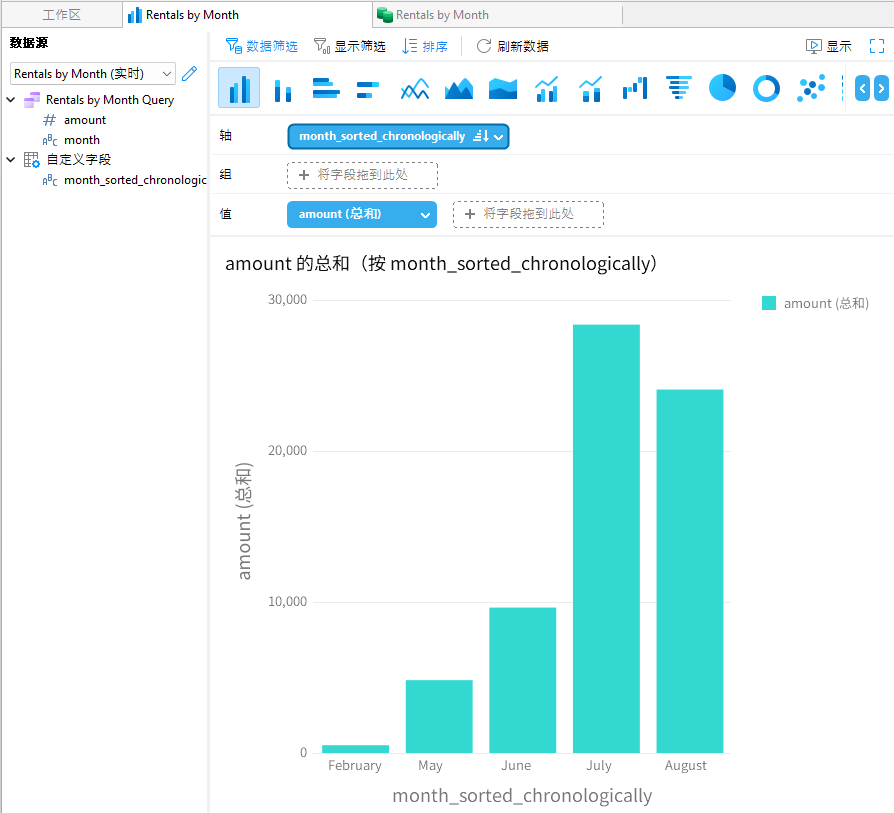
图 3.18 展示了训练网络时损失的变化情况，说明了不同学习率对模型训练的影响。
图 3.19 展示了训练过程中梯度范数的变化，强调了在某些情况下，尽管损失不再下降，但梯度的范数仍然较大。

2. AdaGrad：早期的自适应学习率算法

基本原理：
AdaGrad 是一种根据梯度大小自动调整学习率的算法。其核心思想是：如果某一方向上的梯度较大，那么在该方向上的学习率会逐渐减小，从而避免参数更新过快；反之，如果梯度较小，则学习率会相应增大。

公式：
AdaGrad 更新参数的公式如下：

$\theta_{t+1} \leftarrow \theta_t - \frac{\eta}{\sqrt{G_{t+1}} + \epsilon} g_t$

其中， $G_{t+1}$ 是历史梯度平方和的累积。

图 3.23 解释了为什么不同参数需要不同的学习率，展示了 AdaGrad 如何通过调整学习率来适应不同的梯度。

个人见解：AdaGrad 对于处理稀疏数据（如文本数据）特别有效，因为它能够自动适应每个参数的变化速度。然而，随着训练的进行，学习率会逐渐减小，导致模型在后期可能无法继续有效学习。

3. RMSProp：解决 AdaGrad 的局限性

基本原理：
RMSProp 是对 AdaGrad 的改进，它通过引入指数加权移动平均（Exponential Moving Average, EMA）来平衡历史梯度的影响，从而避免了学习率过早减小的问题。

公式：
RMSProp 的更新公式为：

$\theta_{t+1} \leftarrow \theta_t - \frac{\eta}{\sqrt{\hat{v}_t} + \epsilon} g_t$

其中， $\hat{v}_t$ 是梯度平方的指数加权移动平均， $\eta$ 是学习率。

图 3.25 展示了 AdaGrad 的问题，以及 RMSProp 如何通过动态调整学习率来解决这些问题。

个人见解：RMSProp 能够更有效地应对训练后期梯度变化较小的情况，使得学习率不会过早减小，从而提高了模型的收敛速度。在实践中，RMSProp 是一种常用且稳定的优化算法。

4. Adam：最常用的优化算法

基本原理：
Adam 是目前最常用的优化算法之一，它结合了 RMSProp 和动量（Momentum）的优点。动量通过累积历史梯度来加速收敛，而 RMSProp 则通过动态调整学习率来避免震荡。

公式：
Adam 的参数更新公式为：

$\theta_{t+1} \leftarrow \theta_t - \frac{\eta}{\sqrt{\hat{v}_t} + \epsilon} \hat{m}_t$

其中， $\hat{m}_t$ 是梯度的移动平均， $\hat{v}_t$ 是梯度平方的移动平均。

图 3.26 展示了 RMSProp 的工作原理，强调了通过调整学习率来避免震荡的效果。

个人见解：Adam 由于其强大的适应性和稳定性，几乎成为了深度学习中默认的优化算法。它不仅能够自动调整学习率，还能结合动量来加速模型的收敛，是一种非常有效的优化策略。

5. 学习率调度（Learning Rate Scheduling）

学习率调度的必要性：
即使使用了自适应学习率，在某些情况下，仍然需要手动调节学习率，以便模型更好地收敛。学习率调度是一种常用的技巧，它允许学习率随着训练过程的推进而动态调整，从而更好地适应不同的训练阶段。

常见的调度方法：

学习率衰减：随着训练的进行，逐渐减小学习率，避免训练后期模型的震荡。
预热（Warm-up）：在训练初期，逐渐增大学习率，以便模型在初始阶段更好地适应数据。

图 3.29 展示了学习率衰减的优化效果，说明了如何通过调节学习率来提高模型的收敛速度。

个人见解：学习率调度是提升模型训练效率的有效手段，尤其在训练复杂模型时显得尤为重要。合理的学习率调度能够使模型更快速、更稳定地达到全局最优解。

《深度学习详解》 - 分类问题（Task2.2）

1. 分类问题的定义与特点

分类与回归的对比：
分类与回归都是深度学习中常见的问题类型。回归问题的目标是预测一个连续的数值，而分类问题的目标是将输入数据分配到一组离散的类别中。分类问题可以看作是回归问题的一种特殊情况。

独热编码的使用：
在处理多分类问题时，通常使用独热编码来表示类别标签。独热编码将每个类别表示为一个二进制向量，避免了直接使用数字编码可能带来的类别间无关关系问题。

图 3.30 说明了用数字表示类别可能引发的问题，并介绍了独热编码如何解决这一问题。
图 3.31 展示了网络多输出的示例，解释了如何使用多个输出单元来表示类别。

个人见解：独热编码虽然在多分类问题中非常有效，但其高维度可能会增加模型的计算复杂度。在实际应用中，可以考虑使用嵌入层将高维度的独热编码向量转换为低维度的嵌入向量，从而降低计算成本。

2. 带有 Softmax 的分类

Softmax 函数的作用：
Softmax 是多分类问题中常用的激活函数，它能够将网络的输出转换为概率分布，使得输出值在 0 到 1 之间，并且所有类别的概率和为 1。Softmax 函数的计算公式如下：

$y'_i = \frac{\exp(y_i)}{\sum_j \exp(y_j)}$

Softmax 的效果：
通过将输出值归一化为概率分布，Softmax 函数不仅使输出更直观，还放大了不同类别之间的差异，提高了分类准确性。

图 3.32 说明了 Softmax 在分类问题中的应用，展示了其如何将输出转换为概率分布。
图 3.33 提供了 Softmax 函数的计算示例，展示了不同类别的概率计算过程。

个人见解：Softmax 在多分类问题中非常实用，通过将输出值转换为概率分布，能够使模型更容易地学习和区分不同类别。在二分类问题中，可以直接使用 Sigmoid 函数来替代 Softmax，二者在此情境下的效果是等价的。

3. 分类损失函数

交叉熵损失函数：
在分类问题中，交叉熵（Cross-Entropy）是常用的损失函数。它通过最大化正确类别的概率，来优化模型的参数。交叉熵的计算公式如下：

$e = -\sum_{i} y_i \ln y'_i$

其中， $y_i$ 是真实标签的独热编码， $y'_i$ 是预测的概率分布。

交叉熵 vs 均方误差：
交叉熵相比于均方误差，在分类问题中更常用，因为它能够提供更有效的梯度信号，帮助模型更快地收敛到全局最优解。

图 3.34 展示了分类损失的计算过程，强调了交叉熵在分类任务中的优越性。
图 3.35 对比了使用交叉熵和均方误差进行优化时的梯度变化，展示了交叉熵在分类问题中的优势。

个人见解：在分类问题中，交叉熵通常比均方误差更适合，因为它能够提供更陡峭的损失函数曲线，使得模型在训练过程中更快地更新权重。尤其是在多分类问题中，交叉熵几乎是标准的选择。

总结

通过阅读这两部分内容，我对深度学习中的自适应学习率算法和分类问题有了更深入的理解。自适应学习率算法，如 AdaGrad、RMSProp 和 Adam，能够根据不同参数的梯度动态调整学习率，从而提升模型的训练效果和收敛速度。分类问题中的独热编码、Softmax 函数和交叉熵损失函数则是解决多分类问题的关键工具。

这些知识点为深度学习模型的优化提供了坚实的理论基础，并通过实际案例和图示进一步加深了对这些概念的理解。在未来的深度学习项目中，我将应用这些技术和方法，以提升模型的性能和效率。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/2082457.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！