NLP从零开始------14.文本中阶序列处理之语言模型(2)

3.2 长短期记忆

梯度消失问题的一个解决方案是使用循环神经网络的变体——长短期记忆( long short- term memory, LSTM)。

长短期记忆的原理是，在每一步t，都保存一个隐状态 $h^{t}$ 和一个单元状态( cell state) $c^{t}$ , 通过单元状态来存储长距离信息，长短期记忆模型使用3个门控( gate) 来控制单元状态的读写和擦除。这些门控同样以向量形式表示，其中元素的取值为0或1，0表示门控关闭， 1表示门控打开。门控是动态变化的，每一步都将重新计算门控。

接下来展示长短期记忆模型每一步的具体计算过程。假设第t步的输入为 $x^{t}$ ，隐状态与单元状态分别为 $h^{t}$ 和 $c^{t}$ 。我们依次计算如下向量，所有向量的维度相同。

        遗忘门( forget gate)，控制上一个单元状态中的哪些信息被保留，哪些信息被遗忘：
                                         $f^{(t)}= \sigma (W_{f}h^{(t-1)}+U_{f}x^{(t)}+b_{f})$
        输入门( input gate), 控制哪些信息被写入单元状态:
                                        i⁽ᵗ⁾=σ(Wᵢh⁽ᵗ⁻¹⁾+Uᵢx⁽ᵗ⁾+bᵢ)
        输出门( output gate)，控制单元状态中的哪些信息被写入隐状态：
                                        o⁽ᵗ⁾=σ(Wₒh⁽ᵗ⁻¹⁾+Uₒx⁽ᵗ⁾+bₒ)
新的单元内容，即待写入单元的新信息：
                                         $\tilde {c}^{(t)}= \tanh (W_{c}h^{(t-1)}+U_{c}x^{(t)}+b_{c})$
        单元状态，通过擦除(遗忘)上一个单元状态中的部分信息并写入部分新的信息而获得：
                                         $c^{(t)}=f^{(t)} \odot c^{(t-1)}+i^{(t)} \odot \tilde {c}^{(t)}$
        隐状态，其内容是从单元状态中输出的一部分信息：
                                                h⁽ᵗ⁾=o⁽ᵗ⁾ $\odot$ tanhc⁽ᵗ⁾

其中， $\sigma (x)= \frac {1}{1+ \exp (-x)}$ 为 sigmoid 激活函数, $\tanh (x)= \frac { \exp (x)- \exp (-x)}{ \exp (x)+ \exp (-x)}$ 为 tanh 激活函数,⊙运算为逐元素相乘( element- wise product)。

长短期记忆的模型结构使得跨越多步保存信息变得更为简单直接：如果某一维度的遗忘门打开、输入门关闭，那么单元状态中对应维度的信息就会被完全保存下来。通过这种方式可以跨越多步保留信息，从而更好地建模长距离依赖。而这种跨越多步的状态之间的依赖关系也意味着它们之间存在非零梯度，因而缓解了梯度消失问题。然而，长短期记忆并不能使所有门控会如我们所愿那样打开和关闭，因此不能保证完全没有梯度消失或梯度爆炸的问题，只是长短期记忆在大部分场景中缓解了这些问题。

接下来仿照循环神经网络实现长短期记忆，由于采用同样的接口，我们可以复用之前的训练代码。

# 长短期记忆
def gate_params(input_size, hidden_size):
    return (nn.Parameter(normal((input_size, hidden_size))),
           nn.Parameter(normal((hidden_size, hidden_size))),
           nn.Parameter(torch.zeros(hidden_size)))

class LSTM(nn.Module):
    def __init__(self, input_size, hidden_size):
        super(LSTM, self).__init__()
        self.input_size = input_size
        self.hidden_size = hidden_size
        # 输入门参数
        self.W_xi, self.W_hi, self.b_i = gate_params(input_size, hidden_size)
        # 遗忘门参数
        self.W_xf, self.W_hf, self.b_f = gate_params(input_size, hidden_size)
        # 输出门参数
        self.W_xo, self.W_ho, self.b_o = gate_params(input_size, hidden_size)
        # 候选记忆单元参数
        self.W_xc, self.W_hc, self.b_c = gate_params(input_size, hidden_size)
        
    def init_rnn_state(self, batch_size, hidden_size):
        return (torch.zeros((batch_size, hidden_size), dtype=torch.float),
               torch.zeros((batch_size, hidden_size), dtype=torch.float))
    
    def forward(self, inputs, states):
        seq_len, batch_size, _ = inputs.shape
        hidden_state, cell_state = states
        hiddens = []
        for step in range(seq_len):
            I = torch.sigmoid(torch.mm(inputs[step], self.W_xi) \
                + torch.mm(hidden_state, self.W_hi) + self.b_i)
            F = torch.sigmoid(torch.mm(inputs[step], self.W_xf) \
                + torch.mm(hidden_state, self.W_hf) + self.b_f)
            O = torch.sigmoid(torch.mm(inputs[step], self.W_xo) \
                + torch.mm(hidden_state, self.W_ho) + self.b_o)
            C_tilda = torch.tanh(torch.mm(inputs[step], self.W_xc) \
                + torch.mm(hidden_state, self.W_hc) + self.b_c)
            cell_state = F * cell_state + I * C_tilda
            hidden_state = O * torch.tanh(cell_state)
            hiddens.append(hidden_state)
        return torch.stack(hiddens, dim=0), (hidden_state, cell_state)
    
data_loader = DataLoader(torch.tensor(sent_tokens, dtype=torch.long), 
    batch_size=16, shuffle=True)

lstm = LSTM(128, 128)
train_rnn_lm(data_loader, lstm, vocab_size, hidden_size=128, epochs=200, 
    learning_rate=1e-3)

代码结果：

epoch-199, loss=0.4065: 100%|█| 200/200 [29:26<00:00,  8.83s

        长短期记忆有很多变体，其中一个著名的简化变体是门控循环单元( gated recurrent unit，GRU)。门控循环单元不再包含单元状态，门控也从3个减少到两个。我们同样给出第t步的计算过程，其中输入为 $x^{t}$ ，隐状态为 $h^{t}$ 。
        更新门( update gate)，控制隐状态中哪些信息被更新或者保留：
                         $u^{(t)}= \sigma (W_{u}h^{(t-1)}+U_{ \nu }x^{(t)}+b_{u})$
        重置门( reset gate)，控制前一个隐状态中哪些部分被用来计算新的隐状态：
                                r⁽ᵗ⁾=σ(Wᵣh⁽ᵗ⁻¹⁾+Uᵣx⁽ᵗ⁾+bᵣ)
        新的隐状态内容，根据重置门从前一个隐状态中选择部分信息和当前的输入来计算：
                         $\tilde h^{(r)}= \tanh (W_{h}(r^{(t)} \odot h^{(t-1)})+U_{h}x^{(t)}+b_{h})$

        隐状态，由更新门控制哪些部分来源于前一步的隐状态、哪些部分使用新计算的内容：
                                h⁽ᵗ⁾=(1-u⁽ᵗ⁾)⊙h⁽ᵗ⁻¹⁾+u⁽ᵗ⁾⊙h⁽ᵗ⁾
        下面仿照长短期记忆实现门控循环单元。

# 门控循环单元
class GRU(nn.Module):
    def __init__(self, input_size, hidden_size):
        super(GRU, self).__init__()
        self.input_size = input_size
        self.hidden_size = hidden_size
        # 更新门参数
        self.W_xu, self.W_hu, self.b_u = gate_params(input_size, hidden_size)
        # 重置门参数
        self.W_xr, self.W_hr, self.b_r = gate_params(input_size, hidden_size)
        # 候选隐状态参数
        self.W_xh, self.W_hh, self.b_h = gate_params(input_size, hidden_size)
        
    def init_rnn_state(self, batch_size, hidden_size):
        return (torch.zeros((batch_size, hidden_size), dtype=torch.float),)
    
    def forward(self, inputs, states):
        seq_len, batch_size, _ = inputs.shape
        hidden_state, = states
        hiddens = []
        for step in range(seq_len):
            U = torch.sigmoid(torch.mm(inputs[step], self.W_xu)\
                + torch.mm(hidden_state, self.W_hu) + self.b_u)
            R = torch.sigmoid(torch.mm(inputs[step], self.W_xr)\
                + torch.mm(hidden_state, self.W_hr) + self.b_r)
            H_tilda = torch.tanh(torch.mm(inputs[step], self.W_xh)\
                + torch.mm(R * hidden_state, self.W_hh) + self.b_h)
            hidden_state = U * hidden_state + (1 - U) * H_tilda
            hiddens.append(hidden_state)
        return torch.stack(hiddens, dim=0), (hidden_state,)
    
data_loader = DataLoader(torch.tensor(sent_tokens, dtype=torch.long), 
    batch_size=16, shuffle=True)

gru = GRU(128, 128)
train_rnn_lm(data_loader, gru, vocab_size, hidden_size=128, epochs=200, 
    learning_rate=1e-3)
#%% md

epoch-199, loss=0.2357: 100%|█| 200/200 [38:39<00:00, 11.60s

<Figure size 640x480 with 1 Axes>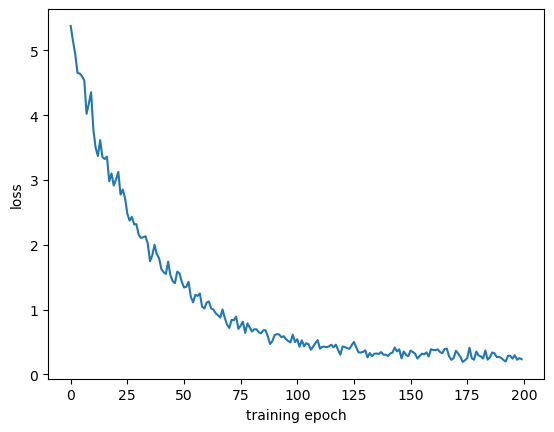

3.3 多层双向循环神经网络

循环神经网络(包括像长短期记忆这样的变体) 可以很方便地扩展为多层和双向结构。
多层循环神经网络将多个循环神经网络堆叠起来，前一层的输出作为后一层的输入，最后一层的输出作为整个模型最终的输出。通过这种方式可以增加整个模型的表达能力，以获得更好的效果，如图所示。

下面在循环神经网络的基础上实现多次循环神经网络。

# 多层循环神经网络
class DeepRNN(nn.Module):
    def __init__(self, input_size, hidden_size, num_layers, dropout=0.):
        super(DeepRNN, self).__init__()
        self.input_size = input_size
        self.hidden_size = hidden_size
        self.num_layers = num_layers
        self._flat_weight_names = []
        self._all_weights = []
        self.drop = nn.Dropout(p=dropout)
        # 定义每一层循环神经网络的参数，由于参数数量不固定，
        # 因此使用统一的命名方法更方便调用和管理
        for layer in range(num_layers):
            W_xh = nn.Parameter(normal((input_size, hidden_size)))
            W_hh = nn.Parameter(normal((hidden_size, hidden_size)))
            b_h = nn.Parameter(torch.zeros(hidden_size))
            layer_params = (W_xh, W_hh, b_h)
            params_names = [f'W_xh_l{layer}', f'W_hh_l{layer}', \
                f'b_h_l{layer}']
            
            # 将新的参数加入到成员列表中
            for name, param in zip(params_names, layer_params):
                setattr(self, name, param)
            self._flat_weight_names.extend(params_names)
            self._all_weights.append(params_names)
            input_size = hidden_size
        self._flat_weights = [getattr(self, wn) if hasattr(self, wn) \
            else None for wn in self._flat_weight_names]
    
    def __setattr__(self, attr, value):
        if hasattr(self, '_flat_weight_names') and \
            attr in self._flat_weight_names:
            idx = self._flat_weight_names.index(attr)
            self._flat_weights[idx] = value
        super().__setattr__(attr, value)
    
    def init_rnn_state(self, batch_size, hidden_size):
        return (torch.zeros((self.num_layers, batch_size, hidden_size), 
            dtype=torch.float),)
    
    def forward(self, inputs, states):
        seq_len, batch_size, _ = inputs.shape
        layer_hidden_states, = states
        layer_h_t = []
        input_states = inputs
        # 需要保存每一层的输出作为下一层的输入
        for layer in range(self.num_layers):
            hiddens = []
            hidden_state = layer_hidden_states[layer]
            for step in range(seq_len):
                xh = torch.mm(input_states[step], 
                    getattr(self, f'W_xh_l{layer}'))
                hh = torch.mm(hidden_state, getattr(self, f'W_hh_l{layer}'))
                hidden_state = xh + hh + getattr(self, f'b_h_l{layer}')
                hidden_state = self.drop(torch.tanh(hidden_state))
                hiddens.append(hidden_state)
            input_states = torch.stack(hiddens, dim=0)
            layer_h_t.append(hidden_state)
        return input_states, torch.stack(layer_h_t, dim=0)

data_loader = DataLoader(torch.tensor(sent_tokens, dtype=torch.long), 
    batch_size=16, shuffle=True)
deep_rnn = DeepRNN(128, 128, 2)
train_rnn_lm(data_loader, deep_rnn, vocab_size, hidden_size=128, 
    epochs=200, learning_rate=1e-3)

epoch-199, loss=0.3928: 100%|█| 200/200 [34:04<00:00, 10.22s

<Figure size 640x480 with 1 Axes>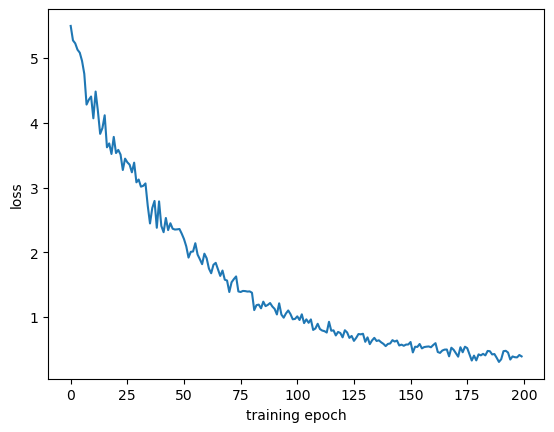

双向循环神经网络的结构包含一个正向的循环神经网络和一个反向的循环神经网络(即从右到左读入文字序列)，将这两个网络对应位置的输出拼接得到最终的输出，如下图所示。

需要注意的是，双向循环神经网络在每个位置的输出同时包含来自左边和右边的信息，也就是整个输入序列的信息，因此双向循环神经网络不能用于语言模型，因为语言模型需要仅根据序列中每个词左边的信息来预测这个词。但是，在后续章节所讨论的很多其他任务中，双向循环神经网络因可以利用整个输入序列的信息而有着比单向循环神经网络更好的表现。
下面的双向循环神经网络是一个简单的示例，要求一次只能输入一个序列。如果想在一个批次中并行处理不同长度的输入序列以获得更高的运行效率，可以通过填充将不同长度的输入序列对齐。单向循环神经网络的填充较为简单，只需在每个序列末尾添加字符。双向循环神经网络的填充更加复杂，正向和反向的循环神经网络的读取顺序相反，难以保证两个方向的循环神经网络都在末尾填充，实现起来较为困难。有关解决方案可以参考PyTorch中的 pack _ padded _ sequence 和 pad _ packed _ sequence。双向循环神经网络不能用于训练语言模型,因此不再提供训练示例代码。

# 双向循环神经网络
class BiRNN(nn.Module):
    def __init__(self, input_size, hidden_size):
        super(BiRNN, self).__init__()
        self.input_size = input_size
        self.hidden_size = hidden_size
        # 正向循环神经网络参数
        self.W_xh = nn.Parameter(normal((input_size, hidden_size)))
        self.W_hh = nn.Parameter(normal((hidden_size, hidden_size)))
        self.b_h = nn.Parameter(torch.zeros(hidden_size))
        # 反向循环神经网络参数
        self.W_xh_reverse = nn.Parameter(normal((input_size, hidden_size)))
        self.W_hh_reverse = nn.Parameter(normal((hidden_size, hidden_size)))
        self.b_h_reverse = nn.Parameter(torch.zeros(hidden_size))
        
    # 分别为正向和反向循环神经网络准备初始状态
    def init_rnn_state(self, batch_size, hidden_size):
        return (torch.zeros((batch_size, hidden_size), dtype=torch.float),
               torch.zeros((batch_size, hidden_size), dtype=torch.float))
    
    def forward(self, inputs, states):
        seq_len, batch_size, _ = inputs.shape
        hidden_state, reverse_hidden_state = states
        hiddens = []
        for step in range(seq_len):
            xh = torch.mm(inputs[step], self.W_xh)
            hh = torch.mm(hidden_state, self.W_hh)
            hidden_state = xh + hh + self.b_h
            hidden_state = torch.tanh(hidden_state)
            hiddens.append(hidden_state)
        reverse_hiddens = []
        for step in range(seq_len-1, -1, -1):
            xh = torch.mm(inputs[step], self.W_xh_reverse)
            hh = torch.mm(reverse_hidden_state, self.W_hh_reverse)
            reverse_hidden_state = xh + hh + self.b_h_reverse
            reverse_hidden_state = torch.tanh(reverse_hidden_state)
            reverse_hiddens.insert(0, reverse_hidden_state)
        # 将正向和反向循环神经网络输出的隐状态拼接在一起
        combined_hiddens = []
        for h1, h2 in zip(hiddens, reverse_hiddens):
            combined_hiddens.append(torch.cat([h1, h2], dim=-1))
        return torch.stack(combined_hiddens, dim=0), ()