以下是提取时间序列分析特征时需要了解的所有内容

时间序列是一种特殊的动物。欢迎来到雲闪世界。

当我开始我的机器学习职业生涯时，我这样做是因为我喜欢物理（开始机器学习的奇怪原因），并且从物理学中我了解到我也非常喜欢编码和数据科学。我并不真正关心数据类型。我只想坐在电脑前每天写 10k 行代码。

事实是，即使你不在乎（我现在仍然真的不在乎），你的职业生涯也会让你关注某些类型的数据而不是其他数据。

如果你在SpaceX 工作，你可能不会做很多 NLP，但你会做很多信号处理。如果你在Netflix工作，你最终可能会接触很多NLP和推荐 系统。如果你在Tesla工作，你肯定会成为计算机视觉专家并从事图像工作。

当我开始以物理学家的身份工作，然后继续攻读工程学博士学位时，我立即被抛入了信号的世界。
这只是工程学的自然世界：每次你设置并从中提取信息时，最终你都会处理一个信号。别误会我的意思，工程学并不是唯一一个以信号为电影明星的世界。另一个非常著名的例子是金融和股票价格的时间序列。这是信号（时间与价格）的另一个例子。但如果出于某种原因你正在处理信号，你应该记住这篇博文的第一句话：

时间序列是一种特殊的动物。

这意味着，许多对表格数据或图像进行的转换/操作/处理技术对于时间序列来说具有另一种含义（如果它们有意义的话）。我们以特征提取为例。

“特征提取”的理念是“处理”我们拥有的数据，并确保我们提取所有有意义的特征，以便下一步（通常是机器学习应用程序）可以从中受益。换句话说，它是一种通过提供重要特征并过滤掉所有不太重要的特征来“帮助”机器学习步骤的方法。

这是完整的特征提取过程：

图片由作者制作

现在，当我们考虑特征提取器（比如表格数据和信号）时，我们正在进行两项完全不同的运动。

例如，峰谷的概念、傅里叶变换或小波变换的概念以及独立 分量分析 (ICA)的概念只有在处理信号时才真正有意义。
我之所以这么说和展示，只是为了让你相信，有一套特征提取技术只属于信号。

现在有两种宏类方法可以进行特征提取：

• 基于数据驱动的方法：这些方法旨在通过查看信号来提取特征。我们忽略机器学习步骤及其目标（例如分类、预测或回归），我们只查看信号、对其进行处理并从中提取信息。
• 基于模型的方法：这些方法着眼于整个流程并旨在找到需要解决的特定问题的特征。

数据驱动方法的优点是它们通常在计算上简单易用，并且不需要相应的目标输出。缺点是这些特征不是针对您的问题的。例如，对信号进行傅里叶变换并将其用作特征可能不是使用在端到端模型中训练的特定特征的最佳方法。

为了这篇博文的目的，我们将只讨论数据驱动方法。具体来说，我们将讨论基于特定领域的方法、基于频率的方法、 基于时间的方法和基于统计的方法。
让我们开始吧！

1. 领域特定特征提取

我要描述的第一个特征有点故意含糊其辞。
事实上，提取特征的最佳方法是考虑你面临的具体问题。例如，假设你正在处理来自工程实验的信号，并且你非常关心t = 6s 之后的振幅。在这些情况下，特征提取通常没有意义（对于随机情况，t=6s 可能并不比 t =10s 更特殊），但它实际上与你的情况极为相关。这就是我们所说的领域特定特征提取。我知道这不需要大量的数学和编码，但这就是它的意义所在，因为它极大地依赖于你的具体情况。

2.基于频率的特征提取

2.1 解释

这种方法与我们的时间序列/信号的频谱分析有关。
这是什么意思呢？如果我们观察信号，我们有一个自然域。自然域是观察信号的最简单方法，它是时间域，这意味着我们将信号视为给定时间的值（或向量） 。

例如，让我们在自然域中考虑这个信号：

如果我们将其绘制出来，我们会得到这样的结果：

图片由作者制作

这是自然（时间）域，也是我们数据集中最简单的域。我们可以在频域中转换它。
正如我们在符号表达式中看到的，我们的信号有三个周期分量。频域的思想是将信号分解为其周期分量频率、幅度和相位。

信号 y(t) 的傅里叶变换Y(k) 如下：

图片由作者制作

这描述了频率为k的分量的振幅和相位。在提取有意义的特征方面，我们可以提取10 个主要分量（振幅最高的分量）的振幅、相位和频率值。这些将是 10x3 特征（振幅、频率和相位 x 10 ），它们将根据频谱信息描述您的时间序列。

现在，这种方法可以扩展。例如，我们可以不基于正弦/余弦函数来分解信号，而是基于小波（另一种周期波形式）来分解信号。 这种分解称为小波分解。

我知道这很难理解，所以让我们从编码部分开始，向你展示我的意思……

2.2 代码

现在，让我们在现实生活中实现它。让我们从非常简单的傅里叶变换开始。

首先我们需要邀请一些朋友参加聚会：

import numpy as np
import matplotlib.pyplot as plt
import pandas as pd

现在我们以此信号为例：

plt.figure(figsize=(10,5))
x = np.linspace(-2*np.pi,2*np.pi,1000)
y = np.sin(x) + 0.4*np.cos(2*x) + 2*np.sin(3.2*x)
plt.plot(x,y,color='firebrick',lw=2)
plt.xlabel('Time (t)',fontsize=24)
plt.xticks(fontsize=14)
plt.yticks(fontsize=14)
plt.grid(alpha=0.4)
plt.ylabel('y',fontsize=24)
Text(0, 0.5, 'y')
Notebook Image

该信号有三个主要分量。一个分量的幅度= 1，频率= 1；一个分量的幅度= 0.4，频率= 2；一个分量的幅度 = 2，频率= 3.2。我们可以通过运行傅里叶变换来恢复它们：

import numpy as np
import matplotlib.pyplot as plt

# Generate the time-domain signal
x = np.linspace(-8*np.pi, 8*np.pi, 10000)
y = np.sin(x) + 0.4*np.cos(2*x) + 2*np.sin(3.2*x)
y= y -np.mean(y)
# Perform the Fourier Transform
Y = np.fft.fft(y)
# Calculate the frequency bins
frequencies = np.fft.fftfreq(len(x), d=(x[1] - x[0]) / (2*np.pi))
# Normalize the amplitude of the FFT
Y_abs = 2*np.abs(Y) / len(x)
# Zero out very small values to remove noise
Y_abs[Y_abs < 1e-6] = 0
relevant_frequencies = np.where((frequencies>0) & (frequencies<10))
Y_phase = np.angle(Y)[relevant_frequencies]
frequencies = frequencies[relevant_frequencies]
Y_abs = Y_abs[relevant_frequencies]

# Plot the magnitude of the Fourier Transform
plt.figure(figsize=(10, 6))
plt.plot(frequencies, Y_abs)
plt.xlim(0, 10)  # Limit x-axis to focus on relevant frequencies
plt.xticks([3.2,1,2])
plt.title('Fourier Transform of the Signal')
plt.xlabel('Frequency (Hz)')
plt.ylabel('Magnitude')
plt.grid(True)
plt.show()

我们可以清楚地看到三个峰值及其对应的振幅和频率。

现在，我们实际上并不需要任何花哨的绘图（这只是为了表明这种方法有效），但我们可以用一个非常简单的函数完成所有事情，这个函数就是这个：

def extract_fft_features( y, x=None,  num_features = 5,max_frequency = 10):
  y= y -np.mean(y)
  # Perform the Fourier Transform
  Y = np.fft.fft(y)
  # Calculate the frequency bins
  if x is None:
    x = np.linspace(0,len(y))
  frequencies = np.fft.fftfreq(len(x), d=(x[1] - x[0]) / (2*np.pi))
  Y_abs = 2*np.abs(Y) / len(x)
  Y_abs[Y_abs < 1e-6] = 0
  relevant_frequencies = np.where((frequencies>0) & (frequencies<max_frequency))
  Y_phase = np.angle(Y)[relevant_frequencies]
  frequencies = frequencies[relevant_frequencies]
  Y_abs = Y_abs[relevant_frequencies]
  largest_amplitudes = np.flip(np.argsort(Y_abs))[0:num_features]
  top_5_amplitude = Y_abs[largest_amplitudes]
  top_5_frequencies = frequencies[largest_amplitudes]
  top_5_phases = Y_phase[largest_amplitudes]
  fft_features = top_5_amplitude.tolist()+top_5_frequencies.tolist()+top_5_phases.tolist()
  amp_keys = ['Amplitude '+str(i) for i in range(1,num_features+1)]
  freq_keys = ['Frequency '+str(i) for i in range(1,num_features+1)]
  phase_keys = ['Phase '+str(i) for i in range(1,num_features+1)]
  fft_keys = amp_keys+freq_keys+phase_keys
  fft_dict = {fft_keys[i]:fft_features[i] for i in range(len(fft_keys))}
  fft_data = pd.DataFrame(fft_features).T
  fft_data.columns = fft_keys
  return fft_dict, fft_data

x = np.linspace(-8*np.pi, 8*np.pi, 10000)
y = np.sin(x) + 0.4*np.cos(2*x) + 2*np.sin(3.2*x)
extract_fft_features(x=x,y=y,num_features=3)[1]

Amplitude 1	Amplitude 2	Amplitude 3	Frequency 1	Frequency 2	Frequency 3	Phase 1	Phase 2	Phase 3
0	1.531008	0.990294	0.983615	3.249675	3.124687	0.9999	-1.56266	1.578706	-1.568175

pip install PyWaveletsPyWavelets

然后运行这个：

import numpy as np
import pywt
import pandas as pd

def extract_wavelet_features(y, wavelet='db4', level=3, num_features=5):
    y = y - np.mean(y)  # Remove the mean

    # Perform the Discrete Wavelet Transform
    coeffs = pywt.wavedec(y, wavelet, level=level)

    # Flatten the list of coefficients into a single array
    coeffs_flat = np.hstack(coeffs)

    # Get the absolute values of the coefficients
    coeffs_abs = np.abs(coeffs_flat)

    # Find the indices of the largest coefficients
    largest_coeff_indices = np.flip(np.argsort(coeffs_abs))[0:num_features]

    # Extract the largest coefficients as features
    top_coeffs = coeffs_flat[largest_coeff_indices]

    # Generate feature names for the wavelet features
    feature_keys = ['Wavelet Coeff ' + str(i+1) for i in range(num_features)]

    # Create a dictionary for the features
    wavelet_dict = {feature_keys[i]: top_coeffs[i] for i in range(num_features)}

    # Create a DataFrame for the features
    wavelet_data = pd.DataFrame(top_coeffs).T
    wavelet_data.columns = feature_keys

    return wavelet_dict, wavelet_data

# Example usage:
wavelet_dict, wavelet_data = extract_wavelet_features(y)
wavelet_data


Wavelet Coeff 1	Wavelet Coeff 2	Wavelet Coeff 3	Wavelet Coeff 4	Wavelet Coeff 5
0	-8.1864	-8.00138	-7.760325	7.65852	7.621079

3.基于统计的特征提取

3.1 解释

特征提取的另一种方法是依靠传统的统计数据。
给定一个信号，可以做多种事情来从中提取一些统计信息。按从简单到复杂的顺序，以下是我们可以提取的信息列表：

• 平均值只不过是信号的总和除以信号的时间步长数。非常简单：

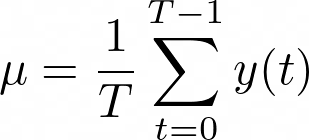
• 方差，即信号与平均值的差异：

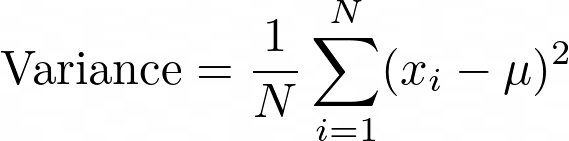
• 偏度和峰度。这些指标用于测试时间序列的分布“非高斯”程度。偏度描述其不对称程度，峰度描述其“尾部”程度。
• 分位数：这些值将时间序列划分为具有概率范围的区间。例如，0.25 分位数，值 = 10，表示时间序列中 25% 的值低于 10，其余 75% 的值大于 10
• 自相关。这基本上可以告诉你时间序列的“模式化”程度，即时间序列中模式的强度。更正式地说，这个指标表示时间序列值与其自身过去值的相关性。
• 熵：表示时间序列的复杂性或不可预测性。我在这里写了一整篇博客文章。

到 2024 年，上述每个属性都可以通过一行代码实现（真是活在当下）。具体方法如下：

import numpy as np
import pandas as pd
from scipy.stats import skew, kurtosis

def extract_statistical_features(y):
    def calculate_entropy(y):
        # Ensure y is positive and normalized
        y = np.abs(y)
        y_sum = np.sum(y)

        # Avoid division by zero
        if y_sum == 0:
            return 0

        # Normalize the signal
        p = y / y_sum

        # Calculate entropy
        entropy_value = -np.sum(p * np.log2(p + 1e-12))  # Add a small value to avoid log(0)

        return entropy_value
    # Remove the mean to center the data
    y_centered = y - np.mean(y)
    y = y+np.max(np.abs(y))*10**-4

    # Statistical features
    mean_value = np.mean(y)
    variance_value = np.var(y)
    skewness_value = skew(y)
    kurtosis_value = kurtosis(y)
    autocorrelation_value = np.correlate(y_centered, y_centered, mode='full')[len(y) - 1] / len(y)
    quantiles = np.percentile(y, [25, 50, 75])
    entropy_value = calculate_entropy(y)  # Add a small value to avoid log(0)

    # Create a dictionary of features
    statistical_dict = {
        'Mean': mean_value,
        'Variance': variance_value,
        'Skewness': skewness_value,
        'Kurtosis': kurtosis_value,
        'Autocorrelation': autocorrelation_value,
        'Quantile_25': quantiles[0],
        'Quantile_50': quantiles[1],
        'Quantile_75': quantiles[2],
        'Entropy': entropy_value
    }

    # Convert to DataFrame for easy visualization and manipulation
    statistical_data = pd.DataFrame([statistical_dict])

    return statistical_dict, statistical_data

y = np.sin(x) + 0.4*np.cos(2*x) + 2*np.sin(3.2*x)
wavelet_dict, wavelet_data = extract_statistical_features(y)
wavelet_data

Mean	Variance	Skewness	Kurtosis	Autocorrelation	Quantile_25	Quantile_50	Quantile_75	Entropy
0	0.00069	2.617477	0.118425	-1.129153	2.617477	-1.330042	-0.086535	1.389426	9.667876

4.基于时间的特征提取器

4.1 解释

在本节中，我们将重点介绍如何通过提取时间特征来提取时间序列的信息。特别是，我们将提取峰和谷的信息。

有多个特征最好了解，以便提取信号的峰值，例如预期宽度、预期阈值或平台大小。如果您有任何此类信息（例如，出于某种原因，您只想考虑振幅 > 2 的峰值），您可以调整参数，否则，您可以将所有参数保留为默认值。

我们还有权决定需要多少个峰值/特征。例如，我们可能想要 N = 10：仅最大的 10 个峰值+谷值。请记住，如果我们这样做，我们就会拥有 Nx2 = 20 个特征（10 个位置和 10 个振幅）。

4.2 代码

与往常一样，实现此目的的代码相当简单：

import numpy as np
from scipy.signal import find_peaks

def extract_peaks_and_valleys(y, N=10):
    # Find peaks and valleys
    peaks, _ = find_peaks(y)
    valleys, _ = find_peaks(-y)

    # Combine peaks and valleys
    all_extrema = np.concatenate((peaks, valleys))
    all_values = np.concatenate((y[peaks], -y[valleys]))

    # Sort by absolute amplitude (largest first)
    sorted_indices = np.argsort(-np.abs(all_values))
    sorted_extrema = all_extrema[sorted_indices]
    sorted_values = all_values[sorted_indices]

    # Select the top N extrema
    top_extrema = sorted_extrema[:N]
    top_values = sorted_values[:N]

    # Pad with zeros if fewer than N extrema are found
    if len(top_extrema) < N:
        padding = 10 - len(top_extrema)
        top_extrema = np.pad(top_extrema, (0, padding), 'constant', constant_values=0)
        top_values = np.pad(top_values, (0, padding), 'constant', constant_values=0)

    # Prepare the features
    features = []
    for i in range(N):
        features.append(top_values[i])
        features.append(top_extrema[i])

    # Create a dictionary of features
    feature_dict = {f'peak_{i+1}': features[2*i] for i in range(N)}
    feature_dict.update({f'loc_{i+1}': features[2*i+1] for i in range(N)})

    return feature_dict,pd.DataFrame([feature_dict])

# Example usage:
x = np.linspace(-2*np.pi,2*np.pi,1000)
y = np.sin(x) + 0.4*np.cos(2*x) + 2*np.sin(3.2*x)
features = extract_peaks_and_valleys(y, N=10)
features[1]

peak_1	peak_2	peak_3	peak_4	peak_5	peak_6	peak_7	peak_8	peak_9	peak_10	loc_1	loc_2	loc_3	loc_4	loc_5	loc_6	loc_7	loc_8	loc_9	loc_10
0	2.89733	2.712237	2.695335	2.694532	2.628401	2.614476	2.308689	2.008004	1.397136	1.37607	924	695	70	539	224	310	454	778	617	148

请记住，如果我们选择 N = 10 个峰值，但您的信号中实际上只有 M = 4 个峰值，则剩余的 6 个位置和峰值幅度将为 0。

5. 使用哪种方法？

好的，我们已经看到了 4 种不同类别的方法。

我们应该使用哪一个？

我不会用“这取决于问题本身”这种外交辞令来打击你，因为当然，这总是取决于问题本身。

事实是，如果您有基于领域的特征提取，这始终是您的最佳选择：如果实验的物理原理或问题的先验知识清晰，您应该依靠它并将这些特征视为最重要的特征，甚至可能将它们视为唯一的特征。有时（很多时候）您没有基于领域的特征，这没关系。

我认为，对于频率、统计和基于时间的特征，你应该将它们一起使用。你应该将这些特征添加到你的数据集中，然后看看其中一些是否有帮助、没有帮助，或者实际上混淆了你的机器学习模型。

6. 结论

非常感谢您抽出时间与我交流。我想借此机会总结一下我们所做的一切。

1. 我们介绍了特征提取的概念。我们解释了它的重要性以及了解时间序列的具体技术的重要性
2. 我们解释了基于模型和数据驱动的特征提取技术之间的区别。基于模型的技术是端到端训练的特征提取技术。在这篇博文中，我们重点介绍了独立于给定任务执行的数据驱动技术
3. 我们讨论了基于领域的特征提取技术，这些技术源于感兴趣的特定问题
4. 我们讨论了频谱技术，这些技术涉及信号的傅里叶/频谱
5. 我们讨论了统计技术，从信号中提取平均值、标准差、熵和自相关的值
6. 我们讨论了基于时间的技术，从信号中提取峰值信息
7. 我们简要介绍了针对您的具体情况应采用哪种 技术

感谢关注雲闪世界。（Aws解决方案架构师vs开发人员&GCP解决方案架构师vs开发人员）

 订阅频道(https://t.me/awsgoogvps_Host)
 TG交流群(t.me/awsgoogvpsHost)