并查集优化策略及其正确性证明:基于路径压缩与按秩合并
- 前言
- 优化策略
- 算法伪代码
- C语言实现
- 归纳法证明
-
- 基础情况
- 归纳步骤
- 结论
前言
引理:对于所有的结点x, 有 x.rank≤x.p.rank, 如 果x≠x.p, 则此式是严格不等 式。x.rank 的初始值为0,并且随时间而增加,直到x≠x.p; 从此以后,z.rank 的值就不再发 生变化。x.p.rank 的值随时间单调递增。这与这引理如何证明呢?

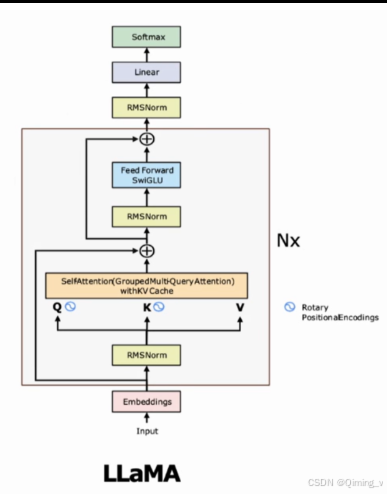
在计算机科学中,这个问题涉及到并查集(Union-Find)数据结构,特别是其路径压缩和按秩合并的优化策略。并查集是一种数据结构,用于处理一些不交集的合并及查询问题。它支持两种操作:
- FIND-SET(x):确定元素x所在的集合的代表,也可以用于确定两个元素是否属于同一集合。
- UNION(x, y):将元素x和元素y所在的集合合并为一个集合。
优化策略
- 路径压缩:在执行FIND-SET操作时,将查找路径上的每个节点都直接链接到根节点,减少树的深度,加快后续查找速度。
- 按秩合并:UNION操作时,将秩较小的树的根节点指向秩较大的树的根节点,这里的“秩”可以定义为树的高度或大小。
算法伪代码
以下是MAKE-SET、FIND-SET和UNION操作的伪代码,包括路径压缩和按秩合并策略: