示波器输出的CSV文件通常包含的是采样的时域信号数据,而不是直接的频率和幅度信息。这个文件一般包括时间(Time)和电压(Voltage)两列,记录了电压随时间变化的情况。
要从这些时域数据中得到频率和幅度的变化,你需要进行一些信号处理,通常步骤如下:
①导入CSV数据:读取CSV文件中的时间和电压数据。
②FFT变换:使用快速傅里叶变换(FFT)将时域信号转换为频域信号,从而得到频率分量和相应的幅度。
③分析频率和幅度:从FFT结果中提取感兴趣的频率分量的幅度,分析其随时间的变化情况。
④绘制频谱图或幅度随频率变化的图:可以绘制频谱图(频率 vs. 幅度)或幅度随时间变化的图来观察频率和幅度的变化。
如果你想直接在CSV文件中看到频率与幅度的变化,通常需要借助一些数据处理工具,比如matlab来进行上述分析并绘图。
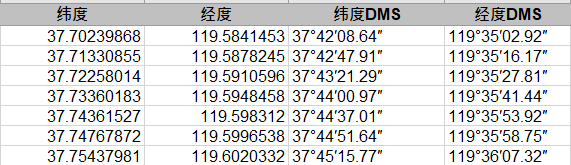
如下图所示,下图为csv文件中一部分数据,其数据表示的是时间(Time)和电压(Voltage)两列,我们需要得到有关频率与幅值的数据,需要进行matlab操作。

可以参考如下程序,自定义选择所需要的csv文件,进行FFT变换得到频谱图,同时生成频谱图所相关的关于频率与幅值的excel表格。
% 让用户交互式选择CSV文件
[file, path] = uigetfile('*.CSV', 'Select the CSV file');
if isequal(file, 0)
disp('User selected Cancel');
else
fullFilePath = fullfile(path, file);
% 读取CSV文件
data = readtable(fullFilePath);
% 假设CSV文件中的时间和电压数据分别在第1列和第2列
time = data{:, 1}; % 读取时间数据
voltage = data{:, 2}; % 读取电压数据
% 检查数据的长度是否为2的幂,如果不是,为了避免频谱泄漏进行截断或填充
N = length(voltage);
N_fft = 2^nextpow2(N); % 获取大于或等于N的最小2的幂
% 计算采样频率
dt = mean(diff(time)); % 计算时间间隔
Fs = 1 / dt; % 采样频率
% 对电压数据进行FFT变换
Y = fft(voltage, N_fft);
% 计算频率向量
f = (0:(N_fft/2-1)) * (Fs / N_fft);
% 计算FFT的幅度
amplitude = abs(Y / N_fft);
% 只取正频率部分
amplitude = amplitude(1:N_fft/2);
% 将频率和幅度数据保存到表格中
T = table(f', amplitude, 'VariableNames', {'Frequency', 'Amplitude'});
% 保存表格数据到Excel文件
[saveFile, savePath] = uiputfile('*.xlsx', 'Save Spectrum Data As');
if isequal(saveFile, 0)
disp('User selected Cancel');
else
writetable(T, fullfile(savePath, saveFile));
disp(['Frequency spectrum data saved to ', fullfile(savePath, saveFile)]);
end
% 绘制频谱图
figure;
plot(f, amplitude);
title('Frequency Spectrum');
xlabel('Frequency (Hz)');
ylabel('Amplitude');
grid on;
end
通过以上代码生成的excel表格及其频谱图如下图所示。