🔥博客主页： 我要成为C++领域大神
🎥系列专栏：【C++核心编程】 【计算机网络】 【Linux编程】 【操作系统】
❤️感谢大家点赞👍收藏⭐评论✍️

本博客致力于知识分享，与更多的人进行学习交流

​

恶魔们抓住了公主并将她关在了地下城 dungeon 的 右下角 。地下城是由 m x n 个房间组成的二维网格。我们英勇的骑士最初被安置在 左上角 的房间里，他必须穿过地下城并通过对抗恶魔来拯救公主。

骑士的初始健康点数为一个正整数。如果他的健康点数在某一时刻降至 0 或以下，他会立即死亡。

有些房间由恶魔守卫，因此骑士在进入这些房间时会失去健康点数（若房间里的值为负整数，则表示骑士将损失健康点数）；其他房间要么是空的（房间里的值为 0），要么包含增加骑士健康点数的魔法球（若房间里的值为正整数，则表示骑士将增加健康点数）。

为了尽快解救公主，骑士决定每次只 向右 或 向下 移动一步。

返回确保骑士能够拯救到公主所需的最低初始健康点数。

注意：任何房间都可能对骑士的健康点数造成威胁，也可能增加骑士的健康点数，包括骑士进入的左上角房间以及公主被监禁的右下角房间。

示例 1：

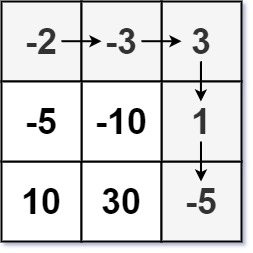
输入：dungeon = [[-2,-3,3],[-5,-10,1],[10,30,-5]]
输出：7
解释：如果骑士遵循最佳路径：右 -> 右 -> 下 -> 下 ，则骑士的初始健康点数至少为 7 。

示例 2：

输入：dungeon = [[0]]
输出：1

提示：

• m == dungeon.length
• n == dungeon[i].length
• 1 <= m, n <= 200
• -1000 <= dungeon[i][j] <= 1000

---

二维动态规划倒推

思路

根据题目的条件可以定义dp[i][j]，表示从左上角到达(i,j)个格子，需要的最低初始血量，但是这样难以确定状态转移方程，因为每次要保证剩余的血量最多以便后续的移动，同时要保证需要的初始血量最少，涉及两个状态转移方程

逆向推导，dp[i][j]表示从(i,j)到达右下角所需要的最低初始血量。

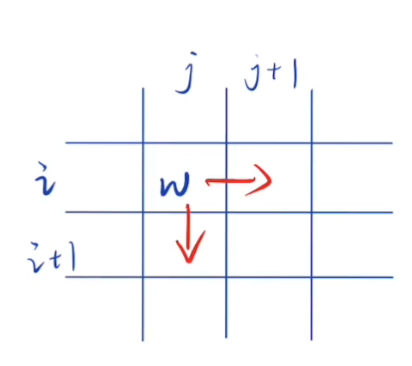
如果是向右移动的话：dp[i][j] + w >= dp[i][j + 1]

如果是向下移动的话：dp[i][j] + w >= dp[i + 1][j]

所以状态转移方程 dp[i][j] = min(dp[i + 1][j], dp[i][j + 1]) - w;

同时为了保证血量大于0，还需要在dp[i][j]和1中取最大值

代码实现

class Solution {
public:
    int calculateMinimumHP(vector<vector<int>>& dungeon) {
        int m = dungeon.size(), n = dungeon[0].size();
        vector<vector<int>> dp(m + 1, vector(n + 1, INT_MAX));
        dp[m][n - 1] = dp[m - 1][n] = 1;
        for (int i = m - 1; i >= 0; --i) {
            for (int j = n - 1; j >= 0; --j) {
                dp[i][j] = min(dp[i][j + 1], dp[i + 1][j]) - dungeon[i][j];
                dp[i][j] = max(dp[i][j], 1);
            }
        }
        return dp[0][0];
    }
};