前面介绍的插值方法，我们可以发现他的特点在于最终得到的曲线一定要经过已经给出的样本点的，而这次要介绍的拟合方法的区别在于，拟合不要求曲线一定要经过所有的样本点，只要这个曲线与样本点之间的误差足够小，距离足够近，这个曲线拟合的效果就足够好，可以使用。

两种方法的对比及引入

        下面是一组数据的分布图，大家可以先观察一下数据的特点。

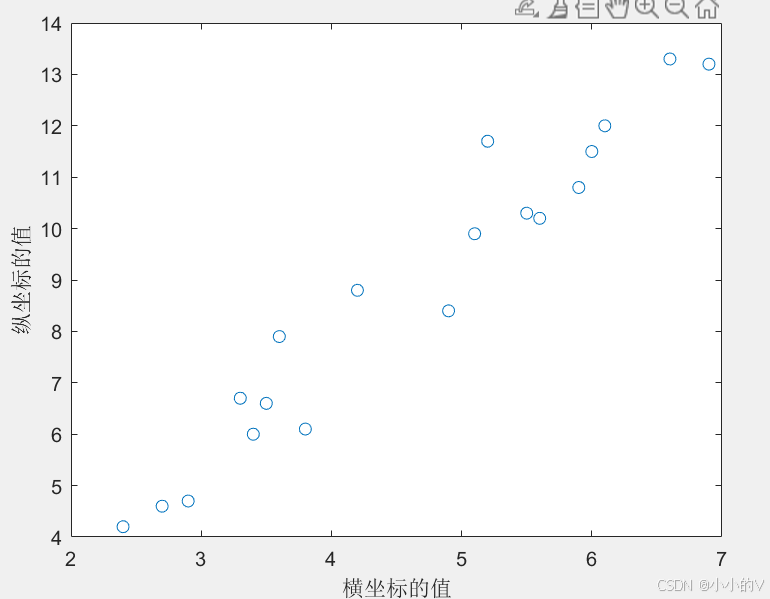
        假如我们想用上次所说的插值的方法来进行补全数据，我们可以使用pchip函数进行三次埃尔米特插值，结果如下。

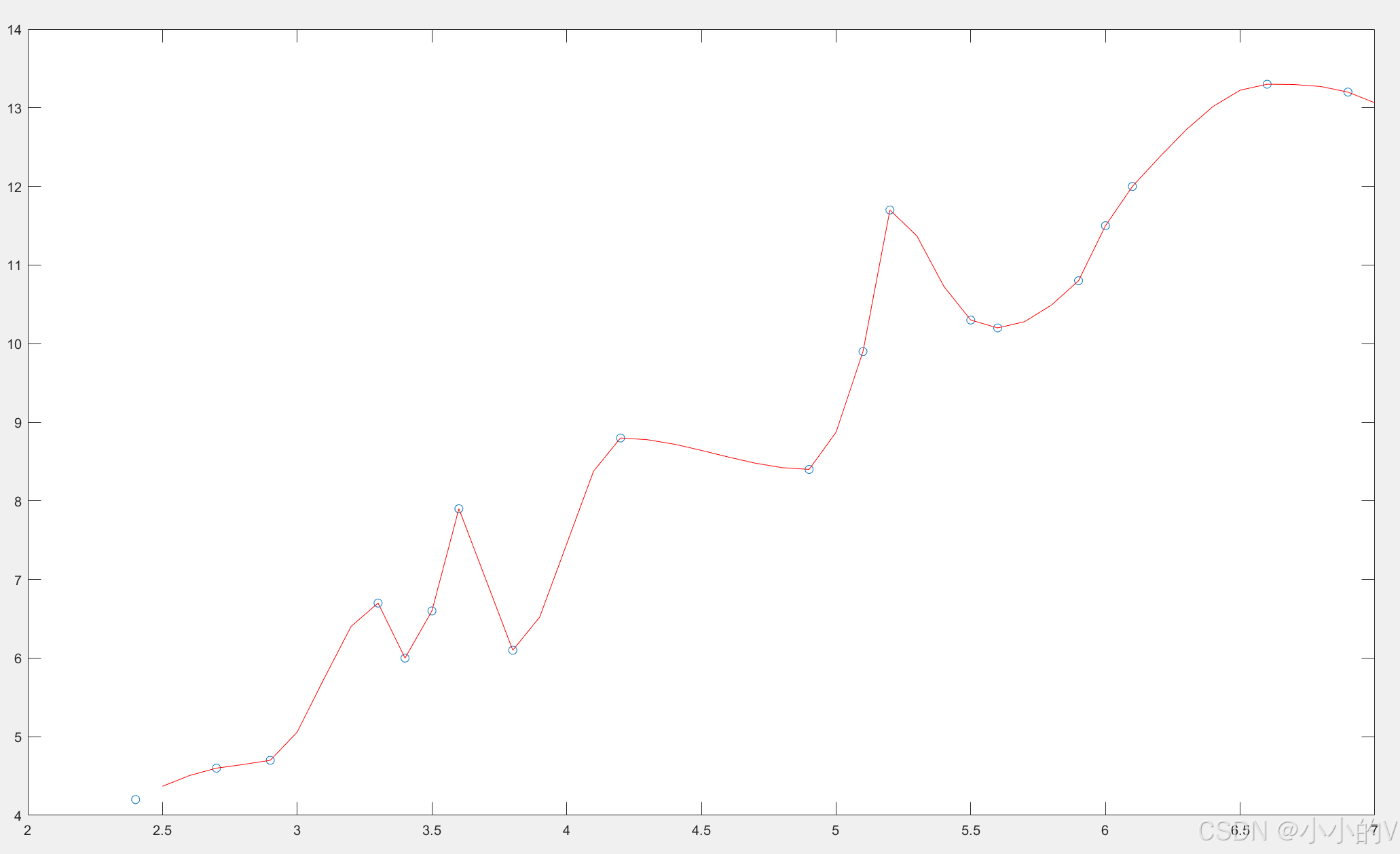
        会发现使用插值法的曲线其实还是比较复杂的，但是如果细心的朋友可能会发现，其实整体的数据的趋势是呈现一个线性上升的趋势的，我们其实可以不需要那么精确的将每一个数据点都覆盖到，使用一个线性的一次函数就可以比较好的对数据的趋势进行一个拟合。

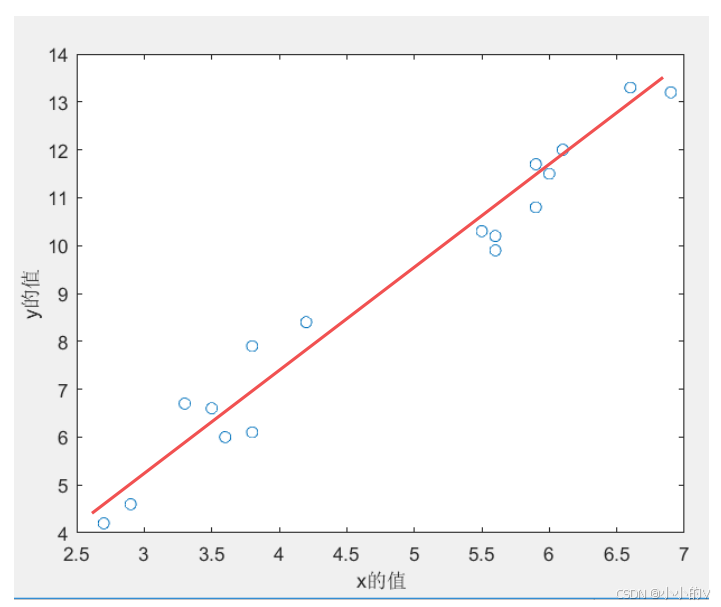
        那么现在接入我们想使用一个一次函数来对数据点进行拟合，我们希望得到最佳的和，使得样本点和曲线之间的整体距离最为接近 。

最小二乘法寻找最优参数

        因此我们采用最小二乘法来获得最优的k和b，最小二乘法的核心公式是这样。

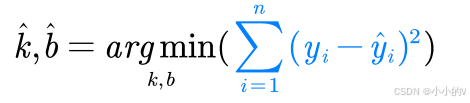
        稍微解释一下，arg代表的意思是寻找参数，没有什么大的影响，是原来的数据点的纵坐标，是拟合曲线上的点的纵坐标。 

        具体得到最优参数的推导过程如下：

        这里稍微对推导过程做一下解释。首先我们将用原来的公式代替，将这些项展开之后，对完整的公式进行求偏导。对k和b分别求偏导数，并将它们设为零。这是基于多元微积分中的极值原理，即在极值点处，所有偏导数都为零。最终通过一系列的化简操作之后就可以得到k和b的表达式。下面就是最终画出来的结果。

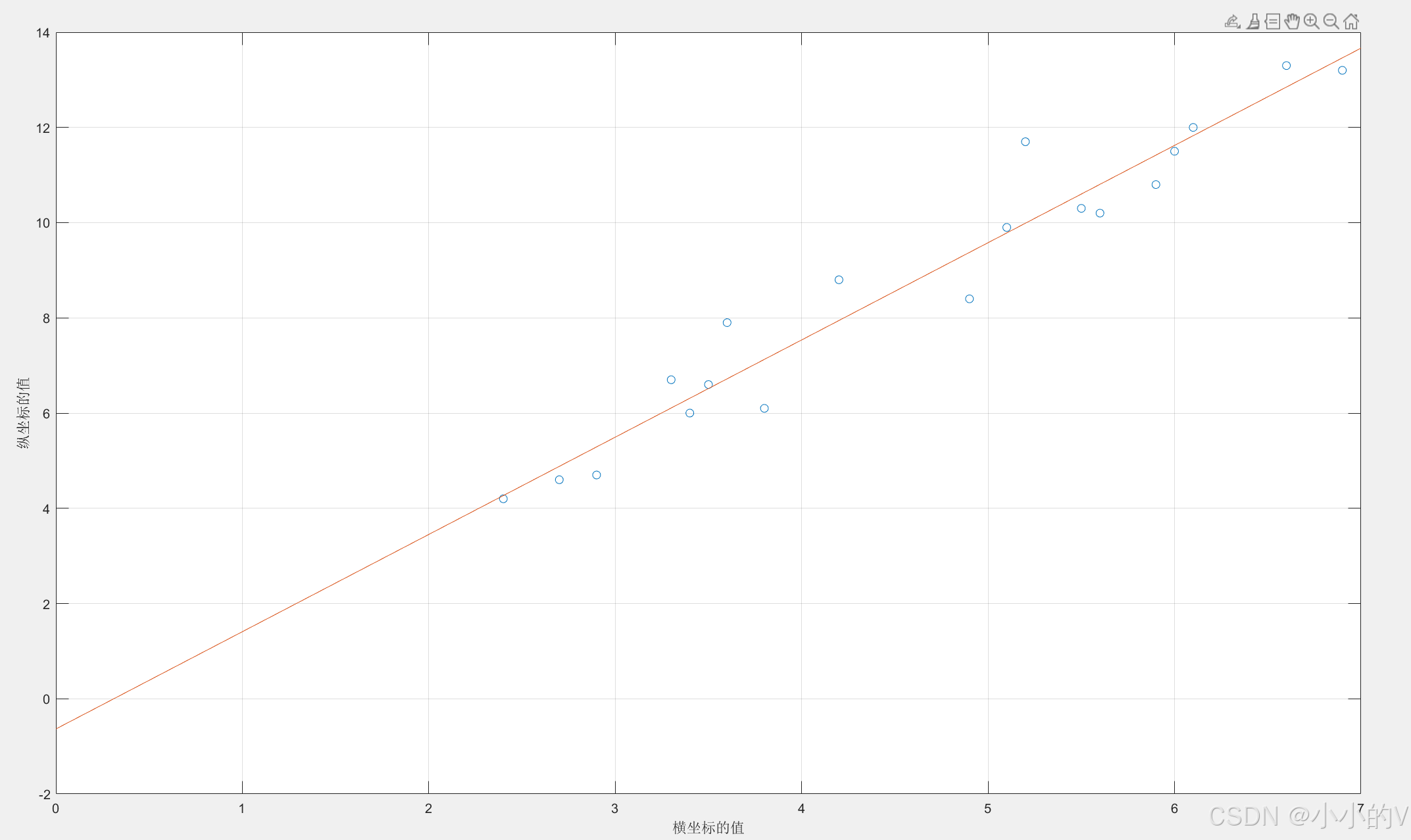
下面是最小二乘法的Matlab代码

x = [4.9, 5.2, 2.4, 3.8, 3.6, 5.6, 6.9, 3.5, 3.4, 2.9, 4.2, 6.1, 5.5, 6.6, 2.7, 3.3, 5.9, 6, 5.1];
y = [8.4, 11.7, 4.2, 6.1, 7.9, 10.2, 13.2, 6.6, 6, 4.7, 8.8, 12, 10.3, 13.3, 4.6, 6.7, 10.8, 11.5, 9.9];
n=size(x,2);%获取数据的长度
plot(x,y,"o");
xlabel("横坐标的值");
ylabel("纵坐标的值"); %这一部分是用来现将原来的数据点画出来的操作
k=(n*sum(x.*y)-sum(x)*sum(y))/(n*sum(x.^2)-sum(x).^2);
b=(sum(x.^2)*sum(y)-sum(x)*sum(x.*y))/(n*sum(x.^2)-sum(x).^2); %求解斜率和截距
hold on  %hold on用来表示下面的画图继续在原来的图上面进行
grid on  %grid on表示显示网格线
f=@(x) k*x+b;   %生成函数，@（x）代表这个函数是以x作为变量
fplot(f,[0,7]); %fplot是用来画函数图像的函数，后面是自变量的范围

误差估计

对拟合的效果进行评估的时候，我们使用来对拟合的效果进行估计。下面介绍一下三个平方和指标，分别是总体平方和（SST），误差平方和（SSE），回归平方和（SSR），是SSR与SST之比。三个的具体内容以及相互之间的关系如下：

下面是误差估计的代码

y_hat=k*x+b;
SSR=sum((y_hat-mean(y)).^2);
SSE=sum((y_hat-y).^2);
SST=sum((y-mean(y)).^2);  %mean函数用来求均值
SST-SSR-SSE
R2=SSR/SST;
disp(R2);

 使用MatLab进行拟合

       我们知道，仅仅使用线性函数的拟合是肯定不够的，对一些规律更加复杂的数据，我们可能需要采用该更加复杂的函数（比如指数函数，高次函数）拟合。Matlab中为我们提供了可以直接帮助我们采用合适的拟合方式的工具，下面来介绍一下。

首先在这里找到画红圈的位置。

开始的界面会呈现下面的这种样子

 找到画红圈的位置，将x和y设置成为你文件中相应的x和y的数据

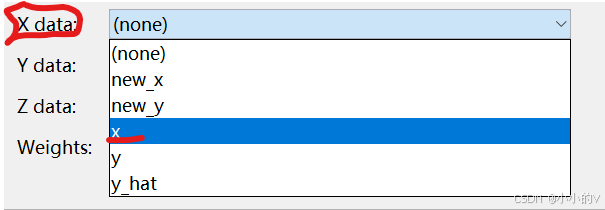
设置好了之后，matlab会自动识别数据的特点并且选择最合适的拟合方法进行拟合。这里采用的是多项式一次拟合（Polynomial，Degree是一次的意思）

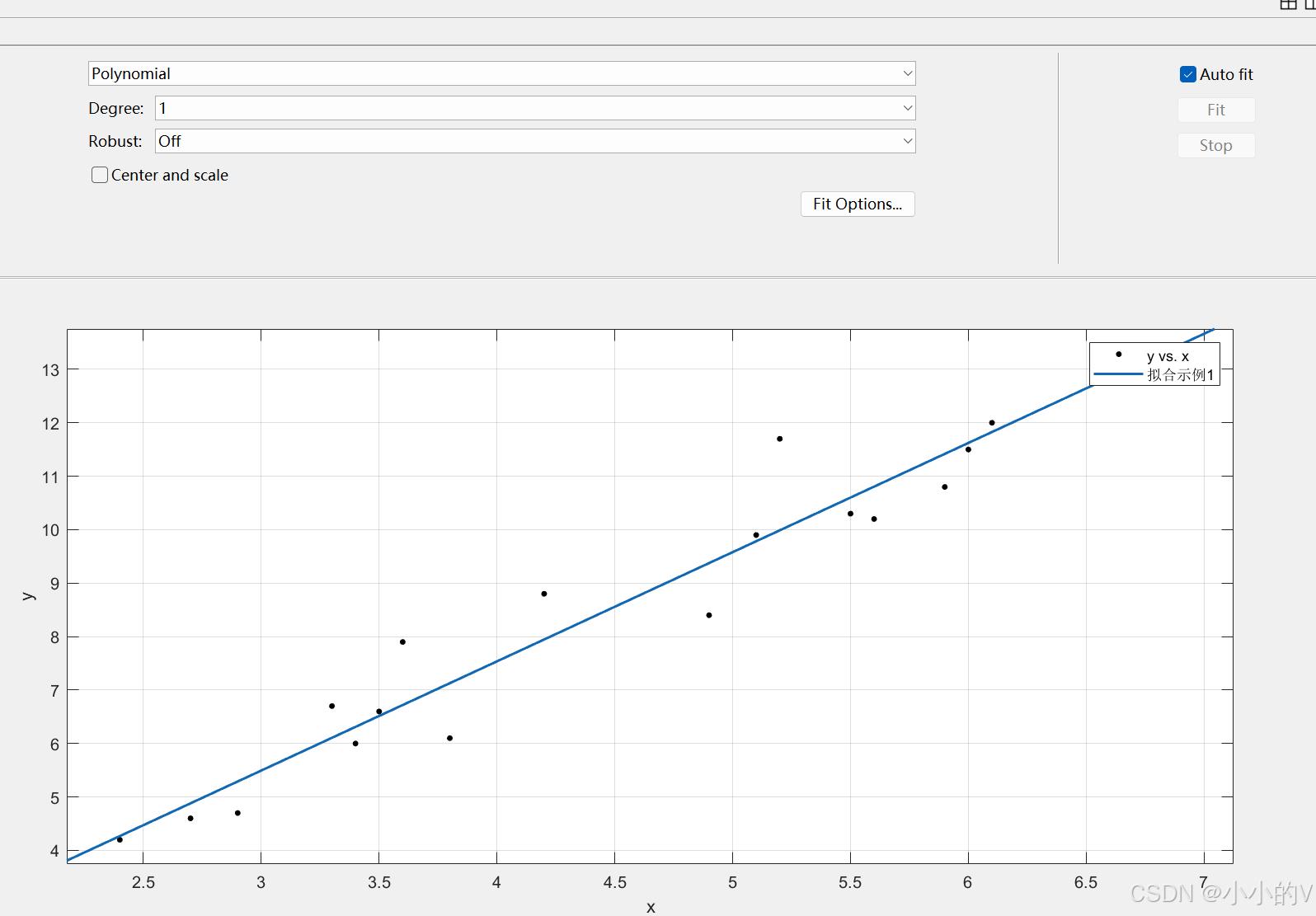
左边的这个部分代表的是各项评估误差的指标，其中就包括我们之前所提到的和SSE，可以看到这里的和1的距离很接近，拟合效果比较好，RMSE也是一个评估拟合精度的指标，大家可以自行了解。

也就是说，拟合工作可以完全由MatLab来帮我们进行实现，MatLab的功能还是太强大了！！

这就是关于拟合的一些介绍，希望对大家有帮助~~