公平组合游戏（Impartial Game）的定义如下：

• 游戏有两个人参与，二者轮流做出决策，双方均知道游戏的完整信息；

• 任意一个游戏者在某一确定状态可以作出的决策集合只与当前的状态有关，而与游戏者无关；

• 游戏中的同一个状态不可能多次抵达，游戏以玩家无法行动为结束，且游戏一定会在有限步后以非平局结束。

博弈图：

        如果将每个状态视为一个节点，再从每个状态向它的后继状态连边，我们就可以得到一个博弈状态图。

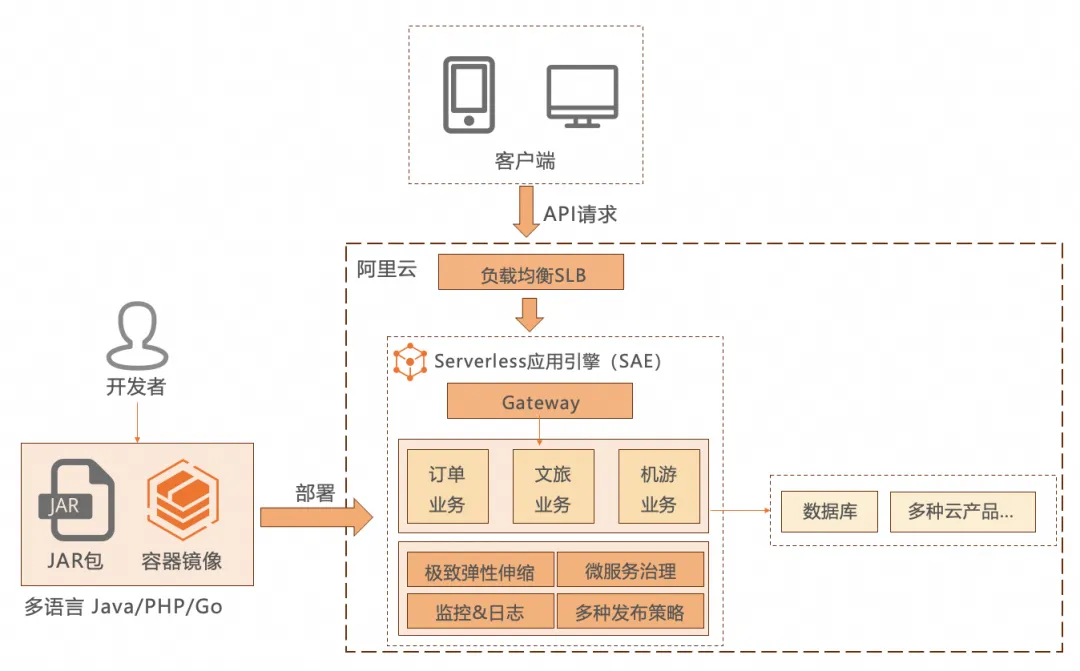
        比如巴什博奕游戏（后面会介绍），我们初始状态设为1堆，3个石头，那么初始状态的博弈图就是：

        3->2 3->1 3->0

        博弈状态关系：

        定义 必胜状态 为 先手必胜的状态，必败状态 为 先手必败的状态。

        从博弈图上可知，状态3一个后继状态为0，而0是必败状态（没有石头，拿不了当然输了），那么3就是一个必胜状态。换句话说，如果当前状态可以到达一个必败状态（不用所有方式，只要有一种），那么当前状态就是必胜状态。反之，如果当前状态只能到达必胜状态（一个必败状态都到不了），那么当前状态就是必败状态。

        上述的必胜状态和必败状态的关系十分重要！！！

 博弈状态关系例题：

题目链接

        假设我们当前处理的值为x0，位置为p，且在p后面还有至少一个x，我们取后面的一个x1。如果x1是必败状态，那么x0就是必胜状态，因为x0可以转移到x1。如果x1是必胜状态，就说明x1可以转移到一个必败状态，且x0也可以转移到该必败状态（因为x0=x1），所以x0是必胜状态。所以只要x0后面仍然有x，那么就是必胜状态。

        如果x后面没有x了。因为只有255个数，所以我们可以遍历找，且我们找的时候也是找每个数（可以转移的数）的最后一个位置（该位置至少要在x的后面），因为不是最后的位置一定是必胜状态。

        代码：

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
//#define int long long
typedef pair<int,int> pii;
const int inf=0x3f3f3f3f;
const int N=2e5+10;
const int mod=1e9+7;
#define fi first
#define se second

int a[N*2];
int pos[400],res[400],vis[400];

int dfs(int x){
	if(vis[x])
		return res[x];
	vis[x]=1;
	int ans=0;
	for(int i=0;i<8;i++){
		int t=x^(1<<i);
		if(vis[t]&&pos[t]>pos[x]) ans|=!res[t];
		else if(pos[t]>pos[x]) ans|=!(dfs(t));
	}
	res[x]=ans;
	return ans;
}

void solve(){
	int n,m,op,k;
	cin>>n>>m;
	for(int i=1;i<=n;i++) {
		cin>>a[i];
		pos[a[i]]=i;
	}
	while(m--){
		cin>>op>>k;
		if(op==1){
			a[++n]=k;
			pos[k]=n;
		}
		else {
			if(pos[a[k]]>k){
				cout<<"Grammy"<<endl;
			}
			else {
				memset(vis,0,sizeof res);
				memset(res,0,sizeof vis);
				if(dfs(a[k])==0) cout<<"Alice"<<endl;
				else cout<<"Grammy"<<endl;
			}
		}
	}
}
signed main(){
	ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
	int t=1;
	//cin>>t;
	while(t--){
		solve();
	}
	return 0;
}

 巴什博弈：

        只有一堆n个物品，两个人轮流从这堆物品中取物，规定每次至少取一个，最多取m个。最后取光者得胜。

        我们用上述的博弈图来解决这个问题。

        假设一开始我们有4个物品，每次最多取3个，有关系如下：

        4->3,4->2,4->1(第一次操作可转移状态)，3->2,3->1,3->0;2->1,2->0;1->0;(第二次操作可转移状态)。容易知道0个物品的时候是必败状态，而1,2,3都能一次转移到0这个必败状态，所以他们都是必胜状态。但是对于4来说，它只能转移到1,2,3状态，也就是说4只能转移到必胜状态，所以4是必败状态。

        n个物品，每次最多取m个的时候同样是这样推理的，然后可以发现m+1 l n（n是m+1的倍数）情况输其他情况都赢，n是石子数，m是每次可取石子数。

威佐夫博弈：

        每次每个人可以从其中一堆石子当中取走任意数量的石子，或者是从两堆当中同时取走相同数量的石子。无法取石子的人落败，请问，在告知两堆石子数量的情况下，这两个人当中哪一方会获胜？

        推理仍然可以用博弈图来推理，但是太繁琐了...

        我们令first的x小于second的y（必败状态是对称的，（x，y）是必败状态，那么（y，x）也是），找一些必败状态(0, 0), (1, 2), (3, 5), (4, 7)...

       

        容易发现他们y-x的差是递增且不相等的，公差为1，也就是y【i】-x【i】=i。

        证明不相等：

        假设有两个必败状态的差值一样，比如（1,2）和（2,3），他们的差值都是1，那么很明显我们可以让（2,3）的两坐标都-1就变成了（1,2），也就是说（2,3）可以到达必败状态，所以他应该是必胜的，所以不可能存在差值相等的两个必败状态。

       

        证明差递增，且公差为1：

        发现x【i】=，y【i】=(是黄金分割率，，后面会求）。有个性质，+1=，那么两边同乘i，再移项得。因为i是整数，这说明i*的小数部分是和i*的小数部分是完全一样的，所以也是成立的。

       

        并且每个必败态的x和y坐标会不重不漏的包括所有正整数（0会出现两次）。

        证明不重：

        令（a，b）为必败状态（b>a），令一个状态为（a，c）。

        c>b时。显然直接让c变成b，就可以到达必败状态，(a,b)。

        c<b时。此时c-a<b-a，也就是说在（a，b）状态之前一定有一个差为（c-a）的必败状态，且（a，c）可以同时减去一个数到达差为c-a的那个必败状态，（x，y）（y-x=c-a，x<a,y<c）。

        令一个状态为（c，b）。

        c>a时。此时b-c<b-a，同样可以在（a，b）前面找到一个必败状态的差为b-c,（x，y）（y-x=b-c，x<c,y<b）。

        c<a时。因为c<a，有两种情况：

        1.如果有以c为前项的必败状态，那么它的y-x值一定是小于b-a的，更小于b-c，所以这种情况只需要让c不动，b减到该值即可，（c，x）（x>c）。

        2.如果是以c作为后项的必败状态，也就是（x，c）（x<c，因为c不在前项就在后项），且（x，c）一定是在（a，b）的前面的，也就是说c-x一定是小于b-a的，同时每个必败状态都是对称的，所以一定存在必败状态（c，x）（x<c），直接让b减到x即可。

       

        证明不漏要用到Beatty定理。

         Beatty 定理:

        若两个正无理数的倒数之和是1，则任何正整数都可刚好(恰好出现一次)以一种形式表示为不大于其中一个无理数的正整数倍的最大整数(向下取整)。

        也就是，且(n,m是正整数)，也就是每个数被其中之一唯一表示。

       

        证明：

        假设不成立，那么存在且。将下取整去掉，等式转化不等式，k<nx<k+1,k<my<k+1(没有等于号因为x，y是无理数).将不等式改变一下，k/n<x<(k+1)/n，都取倒数，因为都是正数，所以不等号取反，即n/k>1/x>n/(k+1),同理可得,m/k>1/y>m/(k+1)，将两个不等式相加，得，(n+m)/k>1/x+1/y>(n+m)/(k+1)，又1/x+1/y=1，所以不等式又变成(n+m)/k>1>(n+m)/(k+1)，再取倒数，同乘（n+m）得，k<n+m<k+1。又因为n+m是整数，所以不等式不成立，即不存在且，所以。

        证明无重复：

        对于，因为x和y都是大于1的数，当n+1的时候，（n+1）x一定比x多1以上，下取整后也会比nx下取整多1以上，不会有重复，my同理，且nx和my下取整无交集。

        证明：

        假设不成立，那么存在且。转换成不等式，nx<k<(n+1)x-1,my<k<(m+1)y-1（因为nx下取整，原式子应该是，因为k是整数,n

x是无理数，举个例子，1<k<3，那么1.5<k<3.5-1=2.5）。和上面一样的变化，n<k/x<n+1-1/x,m<k/y<m+1-1/y，两不等式相加，得，n+m<k<n+m+1。因为k是整数所以不等式不成立，所以。

       

        介绍完Beatty定理回到本题。

        证明不漏（包括所有正整数），并求：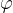

        由α、β两个无理数构成1/α + 1/β = 1，取n为任意正整数且an= ⌊α*n⌋，bn= ⌊β*n⌋（⌊x⌋代表向下取整），序列an和bn就称为Beatty序列。和Beatty序列对比，发现我们的an和bn完全符合Beatty序列，所以an和bn包括了所有正整数。

        计算：已知Beatty序列：an= ⌊α*n⌋，bn= ⌊β*n⌋，而bn = an + n = ⌊α*n⌋ + n = ⌊（α+1）*n⌋，于是β = （α+1），代入1/α + 1/β = 1，解得α =（1+√5）/ 2 ≈ 1.618，这个数字就是黄金比例数。

        

        判断结果：

        因为x=i*，y=i**，所以只要判断（y-x）*==x（i**-i*=i）。

        

        拓展威佐夫博弈：

        两堆拿的值需满足∣ x − y ∣ ≤ d ，可以发现x=n，y=x+（d+1）*n，通过Beatty定理推出

      

        Nim游戏：

        有若干堆石子，每堆石子的数量都是有限的，合法的移动是“选择一堆石子并拿走若干颗（不能不拿）”，如果轮到某个人时所有的石子堆都已经被拿空了，则判负（因为他此刻没有任何合法的移动）。

        结论：

        当且仅当所有堆的石子个数异或和为0时先手必败，其他时候先手必胜。

        

        证明：

        如果当前异或和值为x，比如1010101。我们设y是x的最高位1。因为y是1，就说明一定有某一堆的石子数2进制上y为1，我们设其为z。我们将z的y位以下的2进制数1都取走，我们设这个值是p。那么现在的异或和值为x^p，且x^p的最高位1一定是小于y的，也就是说p>x^p。然后现在我们考虑将p填补石子回z。因为p>x^p，所以我们只需要补回x^p，之后的异或值就为0了。也就是说我们只需要从z堆拿走p-x^p个石子就可以让当前的石子异或为0。

        所以我们总有办法让异或值不为0的状态变成异或值为0的状态，但是如果一开始异或值为0，我们不能让它仍然为0。所以说只要一开始的异或值不为0，先手总可以让异或值变成0，然后后手会让异或值不为0，先手再让异或值为0。一直这样最后先手就会拿光石子。如果一开始异或值为0，后手就可以一直让异或值变成0，最后后手胜。

        

        SG函数：

        含义：

        这个函数的参数是游戏的状态，并且返回值是一个非负整数，当函数值为 0 时，先手必败，否则先手必胜。

        

        mex运算：

        mex表示当前为出现的最小值，比如mex{1 2 3 4 }=0，mex{0 1 2 4 5}=3。

        sg函数计算：

        设当前状态为a，设集合A为a的后继状态集合。那么sg【a】=mex{sg【x1】，sg【x2】....}（x属于集合A），注意一定是由后继状态的sg函数值转移，而不是后继状态的编号。

        

       sg定理：

        一个游戏的sg值等于各个子游戏的sg值异或和

        用sg函数理解Nim和：

        上面证明了Nim和的结论（用结论来证明结论），其实就是利用了sg定理。Nim的n堆石子可以看成n个小游戏（互不影响，比如取了1堆2个石头，并不会影响到2堆和3堆），然后每个小游戏的sg值就是每堆的石子数（举个例子，如果这堆有3个石头，0个石头的sg值为0,1为mex{sg【0】}=1,2为mex{sg【0】，sg【1】}=2,3=mex{sg【0】，sg【1】，sg【2】}），然后把每个小游戏的sg值都异或起来就是Nim游戏的sg值了。

        sg函数例题：

        题目链接

        首先可以发现每个质数是互不影响的，所以每个质数都是一个小游戏，这是一层。对于一个质数x，我们令x的倍数的数为1，其余为0，那么我们就可以得到一个01序列。然后我们每次只能对1的连续序列进行操作，这又是一个小游戏，第二层。对于一个连续序列1，我们发现我们可以从中间取，然后又划分层两侧的连续区间，所以这又是一层小游戏，这是第三层。我们从第三层一直递推到第一层，每次利用sg定理即可。

        注意x^y是可能大于x也大于y的，数组内层要开的大一点，然后要用快速质因数分解。

        代码：

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=1e5+10;
typedef pair<int,int> pii;
const int inf=0x3f3f3f3f;
const int mod=1e9+7;
#define fi first
#define se second
inline int read(){
    int res = 0, ch, flag = 0;
    ch = getchar();
    if(ch==EOF)
    	exit(0);
	if(ch == '-')             //判断正负
        flag = 1;
    else if(ch >= '0' && ch <= '9')           //得到完整的数
        res = ch - '0';
    while((ch = getchar()) >= '0' && ch <= '9' )
        res = res * 10 + ch - '0';
    return flag ? -res : res;
}
inline void print(__int128 x){
	if(x<0){
		putchar('-');
		x=-x;
	}
	if(x>9) print(x/10);
	putchar(x%10+'0');
}

ll gcd(ll a,ll b){
	return b==0?a:gcd(b,a%b);
}

ll q_pow(__int128 a,ll b,ll mo){
	ll res=1;
	while(b){
		if(b&1) res=((__int128)res*a)%mo;
		b>>=1;
		a=((__int128)a*a)%mo;
	}
	return res%mo;
}

bool MillerRabin(ll n){
	if(n==2) return 1;
	if(n<=1||n%2==0) return 0;
	ll base[]={2,325,9375,28178,450775,9780504,1795265022};//或前12个素数 
	ll u=n-1,k=0;
	while(u%2==0) u/=2,k++;
	for(auto &x:base){
		if(x%n==0) continue;//n的倍数不可以用 
		ll v=q_pow(x,u,n);//x^u
		if(v==1||v==n-1) continue;//-1 1 1 1 1，1前面只能是-1 
		for(int j=1;j<=k;j++){
			ll last=v;
			v=((__int128)v*v)%n;//x^2u->(x^u)^2,x^4u->((x^u)^2)^2,x^8u->(((x^u)^2)^2)^2
			if(v==1){
				if(last!=n-1) return 0;
				break;
			}
		}
		if(v!=1) return 0;//x^(n-1)%n=1 
	}
	return 1;
}

ll Pollard_Rho(ll n){//找一个n的约数 
	static mt19937_64 sj(chrono::steady_clock::now().time_since_epoch().count());
	uniform_int_distribution<ll> u0(1,n-1);
	ll c=u0(sj);
	auto f=[&](ll x){
		return ((__int128)x*x+c)%n; 
	};
	ll x=0,y=0,s=1;
	for(int k=1;;k<<=1,y=x,s=1){
		for(int i=1;i<=k;i++){
			x=f(x);
			s=(__int128)s*abs(x-y)%n;
			if(i%127==0){
				ll d=gcd(s,n);
				if(d>1) return d;
			}
		}
		ll d=gcd(s,n);
		if(d>1) return d;
	}
	return n;
}

vector<ll> factor;//每次用factor要清空 
void get_factor(ll n){//25会放入5*5，因子有重复 
	if(n==1) return;//1不是质数 
	if(MillerRabin(n)){
		factor.push_back(n);//放入质数因子 
		return;
	}
	ll x=n;
	while(x==n) x=Pollard_Rho(n);//n不是质数，一直找到一个约数 
	get_factor(x),get_factor(n/x);//把n分解成约数x和n/x 
}

map<ll,vector<ll> > pos;
set<ll> s;
ll n,a[N];
ll sg[N];

void init_sg(int n){
	sg[0]=0,sg[1]=1;
	for(int i=2;i<=n;i++){
		vector<bool> vis(n*5);
		for(int j=0;j<=i;j++){
			for(int k=0;k+j<=i;k++)
				vis[sg[j]^sg[k]]=1;
		}
		for(int j=0;;j++){
			if(!vis[j]){
				sg[i]=j;
				break;
			}
		}
	}
}

void work(int i){
	factor.clear();
	get_factor(a[i]);
	sort(factor.begin(),factor.end());
	factor.erase(unique(factor.begin(),factor.end()),factor.end());
	for(auto &x:factor){
		s.insert(x);
		pos[x].push_back(i);
	}
}

void solve(){
	cin>>n;
	init_sg(n);
	for(int i=1;i<=n;i++){
		cin>>a[i];
		work(i);
	}
	ll ans=0;
	for(auto &x:s){
		int sum=0,last=-1,tempsg=0;
		for(auto &y:pos[x]){
			if(last==-1||y==last+1){
				sum++;
			}
			else{
				tempsg^=sg[sum];
				sum=1;
			}
			last=y;
		}
		tempsg^=sum;
		ans^=tempsg;
	}
	cout<<(ans?"First":"Second")<<endl;
}
int main(){
	ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
	int t=1;
	//cin>>t;
	while(t--){
		solve();
	}
	return 0;
}

        

        对称操作博弈：

        硬币问题：

        5个硬币围成一圈，每次只能取连续的1-2个（如果一开始是123，那么12连续，23连续，13不连续，把2取掉变成1 3，13还是不连续的），取完获胜，谁赢？

        只要后手一直模仿先手的操作，每次都留下对称的部分，那么后手一定胜，就算一开始5并不对称，但可以通过拿1个（先手第一次拿2个，后手拿那两个的对面的一个），或者拿2个（先手第一次拿1个，后手拿那一个的对面的两个），来保证剩下两个硬币不连续（也就是对称的），不让先手一次拿完就赢了。

        扩大范围n个硬币，每次只能取连续1-k个，如果k>=n先手胜，如果k==1看n的奇偶，其余只要后手都执行对称操作，后手一定胜。

        台阶问题：

        现在有3个台阶，从低到高每个台阶都有一些石子，个数分别为{1,2,3}，可以从某一台阶挑选任意个石子扔到下一层台阶，扔到地上的台阶不能再操作，不能操作的人输，两个人轮流操作，谁赢？

        可以发现，对于先手操作偶数层的情况，后手一定可以对称操作，比如先手从x层扔y个石子到x-1层，那么后手一定可以从x-1层扔y个石子到x-2层，最后后手会将石子扔到地面上。也就是说无论偶数层有多少石子，哪些偶数层有石子，哪些偶数层没有石子，实际上并不会影响结果，因为后手一定可以采取对称操作。

        所以只需要考虑奇数层石子数。假如x层有y个石子（x是奇数），那么先手可以取任意个扔到x-1层（x-1是偶数），设扔的个数是z（z<=y）。那么会发现这z个石子到偶数层以后双方又可以采用对称操作，也就是说这z个石子一定会被扔到地上，且扔到地上以后是由后手开始下一轮操作。也就是说实际上问题就转化成每个奇数层阶梯有一些石子，然后两个人轮流从奇数阶梯挑一些石子扔到地上（扔到下一偶数层等价扔到地上），这就变成奇数层上的Nim游戏，所以只需要对奇数层取异或和即可。

       图的博弈：

        树上删边博弈：

        给出一个有根树，游戏者轮流从树上删去一条边，删去一条边后，不与根连通的部分被删去，谁不能操作谁输。

        

        与Nim游戏的关系：

        当一颗树退化成一条链的时候，容易发现这就是一个只有一堆石子的Nim游戏。如果有多条链，那么就是一个普通的Nim游戏。但是当两条链连接后又有所不同（不一定两端相连），这里要用到克朗原理。

        

        克朗原理：

        对于树上的某一个点，它的子树可以转化成以这个点为根的一条链，这个链的长度就是它各个链里边（一定是先变成链之后的边）的数量的异或和。

        

        sg函数和链边个数的关系：

        也就是说对于一个根节点，它和它的子树可以看成一条链，链长就是以根的每个直接儿子及其子树所构成的链里边的数量的异或和（就是一直递归下去，让每个子树最后合成一整条链），但是实际上一个点以及它子树所构成链的边个数就是这个点的sg值。

        叶子节点sg值是0，两个节点的链sg值是1，3个节点的链的sg值是2....就是Nim游戏的sg值。设根节点为x，它有3个儿子，s1，s2，s3，那么sg【x】=（sg【s1】+1）^（sg【s2】+1）^（sg【s3】+1）。sg【s】的时候已经是把儿子节点及其子树变成链了，且链里边的个数就是sg【s】，因为根节点x与儿子也有一条边，所以是sg【x】+1才是以x为根的链里边的个数。

        一般图的删边博弈：

        就是可能有环的树上删边博弈。

        

        对于环的处理：

        对于偶数边的环我们可以对称操作，和上面说的硬币一样，只是每次只能删一个边，最后会发现偶数边的环对结果没有影响，所以我们把偶数环缩成一个点。

        对于奇数边的环我们仍然对称操作，最后对结果等价多一条边的影响，所以将奇数环缩成一条边加一个点。

        处理完环就变成树上博弈了。