全文链接:https://tecdat.cn/?p=37423
分析师:Greata Xie
“你的命运早在出生那一刻起便被决定了。”这样无力的话语,无数次在年轻人的脑海中回响,尤其是在那些因地域差异而面临教育资源匮乏的年轻人中更为普遍。在中国,这种现象尤为明显:没有生在大城市的他们,从小便需面对教育资源的不平等,有人甚至在初中阶段便被迫放弃学业,转而在流水线旁成为普工;而即便有幸成为家乡的佼佼者,他们长大后也可能因户口问题而选择低薪工作,或是将收入的一半付给房东(点击文末“阅读原文”获取完整代码数据)。
然而,当我们跨越国界,来到高度发达的英国,却发现类似的问题依旧存在。一项发表在《城市经济学》上的研究,通过对英国7500名居民长达近二十年的追踪调查,揭示了原生城市规模对个人成年后收入的深远影响。研究发现,与曼彻斯特和利物浦相比,伦敦出生的居民平均收入更高,这一发现无疑加剧了小城市居民的心理压力。
但幸运的是,研究并未止步于此。为了进一步量化各变量对收入的影响,研究者们应用了复杂的计量方法。他们发现,“学习”(即工作后获得的知识和经验积累)在原生城市规模对收入的影响中占据了高达65.2%的比重,而教育和当前工作城市规模则分别占据了10.9%和8.6%的比重。
在数据时代,我们更应该重视数据的作用,通过构建精确高效的模型来预测和解释个人收入的差异。
为此,我们通过分析多种影响收入的数据,构建影响个人收入的模型,采用了多种建模方式,包括线性回归、决策树、梯度提升、岭回归等,并通过测试数据回测选出了表现最好的模型。
任务/目标
通过分析多种影响收入的数据(查看文末了解数据免费获取方式),构建影响个人收入的模型,实现对个人收入预测,并根据模型结果为教育部等相关部门提出建议。
数据源准备
有相关数据的详细披露,需要将目标数据爬取或直接下载。
数据清洗
但经过python相关函数的检测,我们发现很多空数据,由于模型和数据涉及的影响变量较多,所以出现空数据的个体无法参与到所有因素的建模中。
但若去掉携带空数据的个体后数据分布发生变化,则使用去掉空数据后建立的模型就无法准确预测整体样本,面对这个问题,我们对比了完整样本和去掉空数据后样本的柱状图,证明了去掉空数据并不会影响样本的整体分布。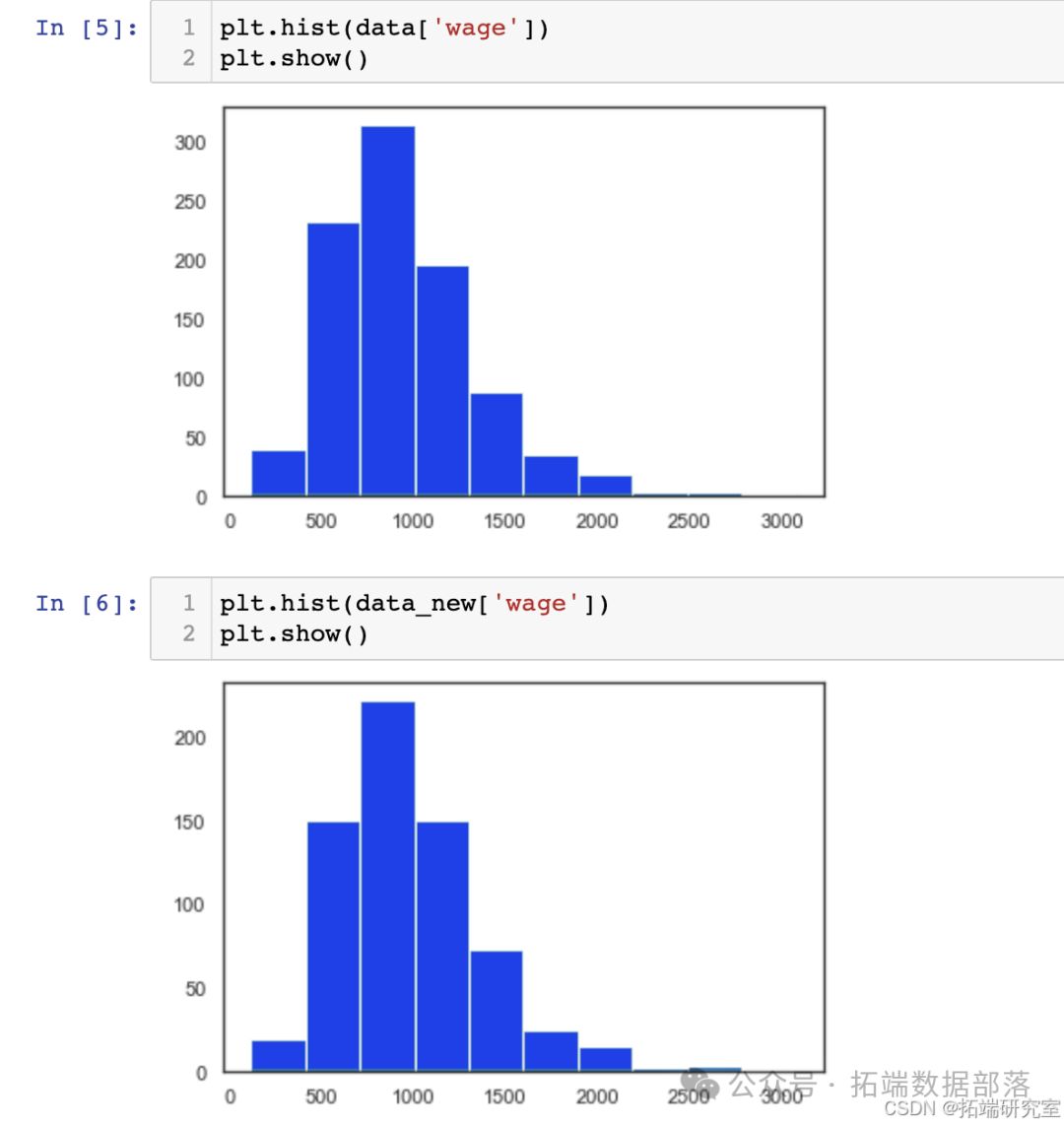
构造
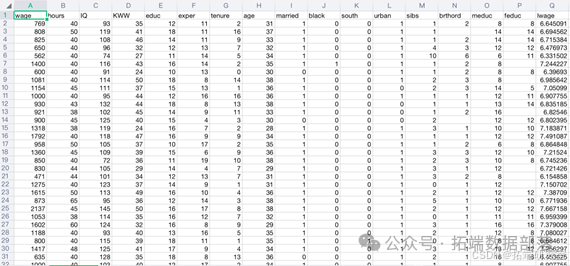
样本中一共收集了935个人的16项不同的相关数据。
去掉空数据后新样本一共收集了663个人的16项不同的相关数据。
划分训练集和测试集
由于相关部门的数据披露并没有时间顺序,所以为了建立真实和无偏差的测试模型,我们以8:2的分数形式对数据样本切分训练集和测试集。具体做法如下:
我们一共有663份相关数据,随机抓取530份数据作为training data(即训练数据),剩下的133份数据作为testing data(即测试数据)。
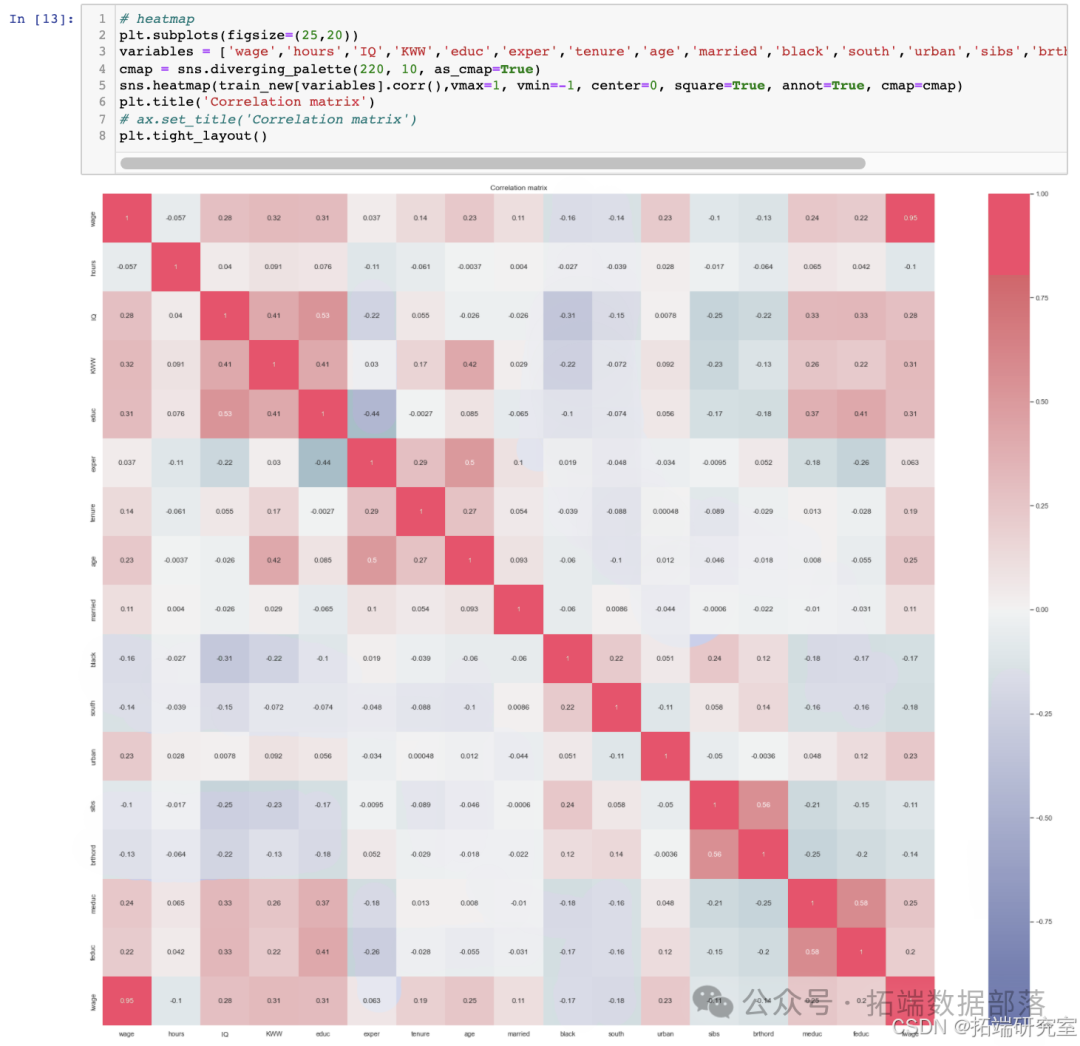
探索性分析
利用成对分析和热力图,对大量的变量和数据之间的关系进行观察和预测。
点击标题查阅往期内容

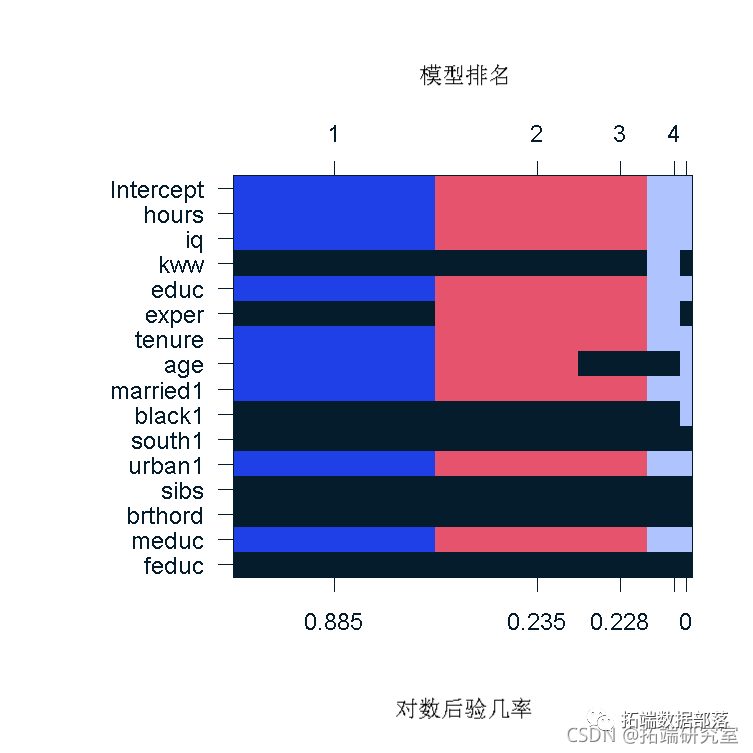
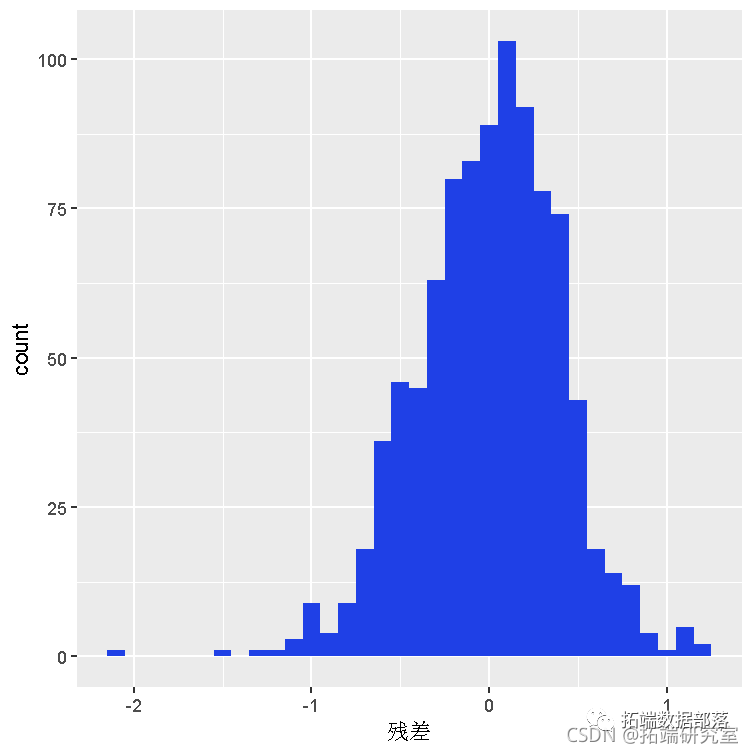
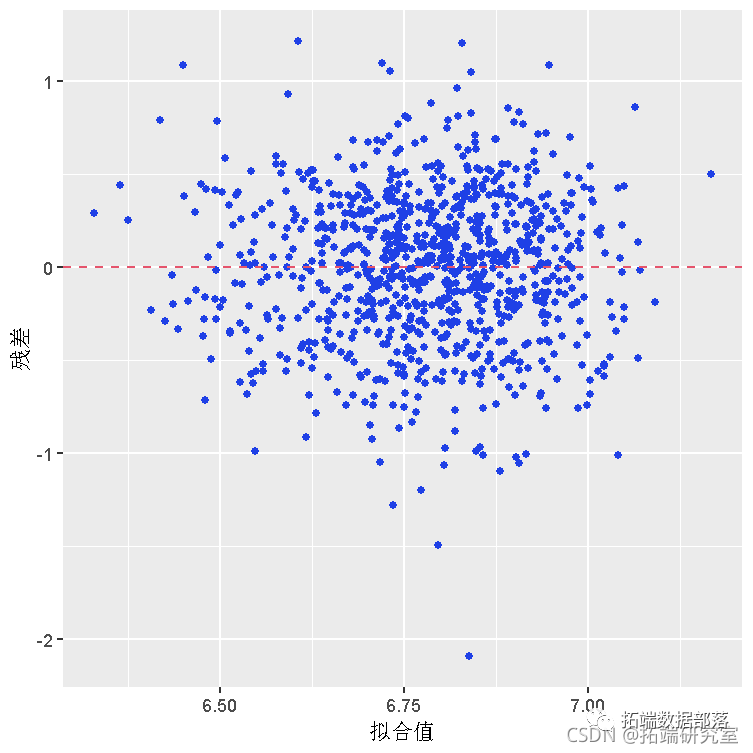
R语言用贝叶斯线性回归、贝叶斯模型平均 (BMA)来预测工人工资

左右滑动查看更多

01
02
03
04
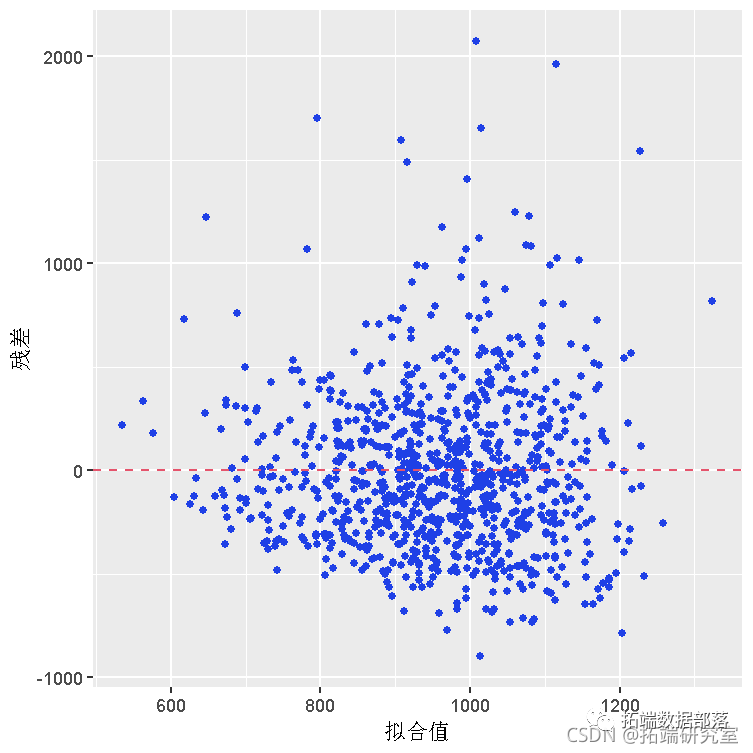
建模
由于变量数过大,我们对训练数据采用了简单线性回归、多重线性回归、线性样条、带多个节点的线性样条、多项式回归、变量间相互作用、对数转换、指数转换等多个建模方式,并定义前向选择和逆向选择的函数,协助进行高效建模,最终从20多个模型中选取表现最好的前八个模型。
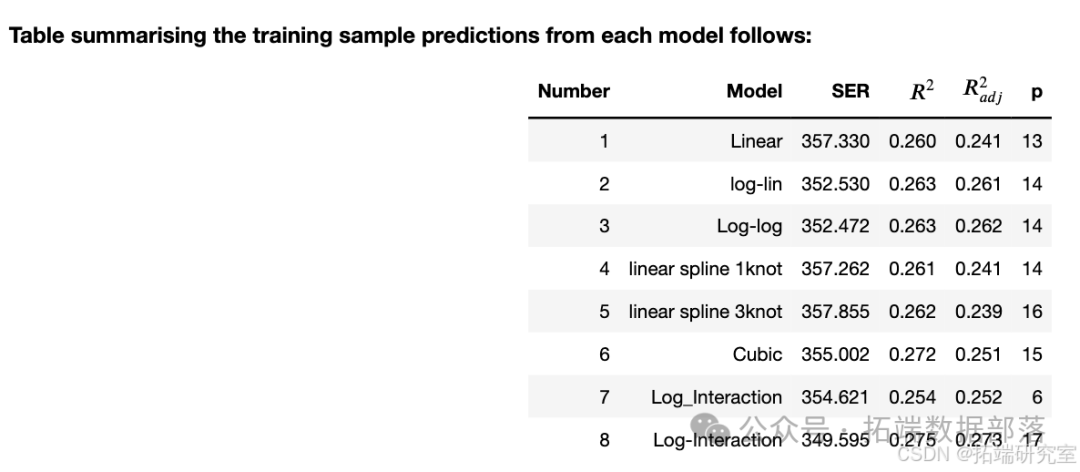
模型选取
通过使用测试数据进行回测,选择在测试数据中表现最好的模型
在此项目中,经过测试数据的回测,选出的8个模型中,标记为log-interaction11的模型表现最好,表现最好的前三个模型拟合情况对比图如下:
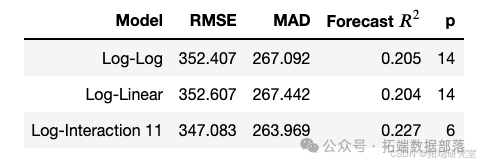
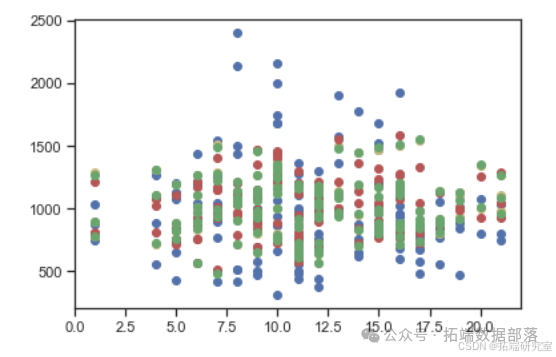
log-interaction11采用正常最小二乘方回归的方程结果如下:

教育、工作经验、是否结婚和是否在城市生活的交互作用、年纪和知识面的交互作用、智商和母亲教育程度的交互作用、教育和是否为黑种人的交互作用组成了最终预测工作水平准确度最高的模型。
Python对工资影响的回归分析及偏差探讨|附代码数据
接下来,我们将尝试估算多接受一年教育对小时工资的影响。进行教育实验是非常困难的。你不能简单地将人们随机分配到 4 年、8 年或 12 年的教育。
model_1.summary().tables\[1\]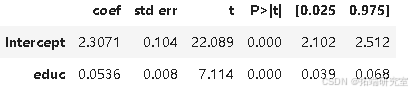
对工资与教育年限进行简单回归,估计出回归系数 β1 为 0.0536,95% 置信区间为 (0.039, 0.068)。这意味着该模型预测每增加一年教育,工资将增长约 5.3%。
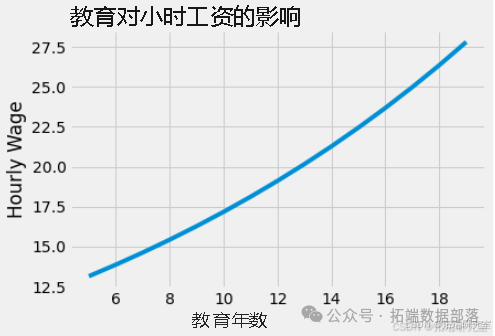
仅考虑教育变量的简单模型可能存在偏差。首先,数据并非来自随机实验,接受更多教育的人与接受较少教育的人可能不可比。其次,从对世界的理解来看,受教育年限更多的人可能有更富裕的父母,工资随教育增加可能只是家庭财富与教育年限相关的反映。此外,教育也可能因让人远离劳动力市场而降低工资。
引入其他变量的多元回归分析
(一)变量选择
在数据中,我们可以获得其他变量,如父母教育程度(meduc、feduc)、个人智商(IQ)、工作经验(exper)、任期(tenure)以及婚姻和种族的虚拟变量等。
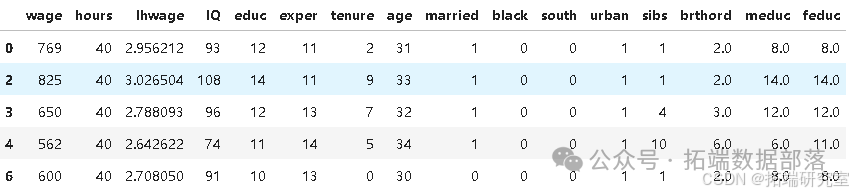
kappa = t\_tilde.cov(y) / t\_tilde.var()kappa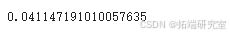
通过引入这些变量进行多元回归分析,估计出在控制其他因素后,每增加一年教育与小时工资增长 4.11% 相关。这证实了简单模型存在偏差且高估了教育的影响。
model_2.summary().tables\[1\]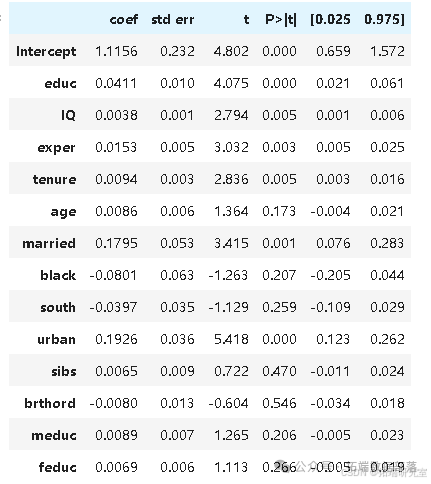
遗漏变量或混杂偏差
偏差来源
以教育对工资的影响为例,未控制智商等变量时,教育对工资的影响也包含了其他未纳入模型变量的影响,这是遗漏变量偏差的来源,即混杂变量影响了处理变量和结果变量。
g.edge("Police", "Violence", color="blue")g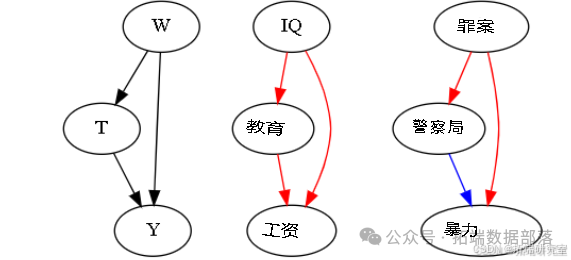
因果图分析
以教育对工资的影响为例,因果图显示教育导致工资,同时智商也导致工资和教育。如果不考虑智商变量,其对工资的影响会通过与教育的相关性使教育对工资的影响看起来比实际更高,这是正偏差的例子。
以警察对城市暴力的影响为例,城市警力增加与暴力增加相关,但可能存在混杂变量犯罪,犯罪导致更多暴力和更多警力。如果不考虑犯罪变量,犯罪对暴力的影响会通过警力使警力看起来增加了暴力,这是负偏差的例子。

Python机器学习:回归、决策树、梯度提升、岭回归薪资预测分析|附代码数据
接下来本文对 数据集进行了全面分析,旨在基于年龄、工作年限、性别和职位等多个特征来预测薪资。通过广泛的数据处理、可视化以及机器学习方法,我们获得了有价值的见解并构建了具有高准确性的预测模型。
数据处理流程定义
(一)使用 ColumnTransformer 进行数据预处理
确定分类特征和数值特征,分类特征包括 “Gender”(性别)、“Education Level”(教育水平)、“Job Title”(职位),数值特征包括 “Age”(年龄)、“Years of Experience”(工作年限)。
import numpy as npcat\_features = \['Gender', 'Education Level', 'Job Title'\]num\_features = \['Age', 'Years of Experience'\]定义超参数分布字典
为不同的回归模型定义超参数分布字典,例如 “LinearRegression”(线性回归)和 “DecisionTreeRegressor”(决策树回归器),设置不同的超参数取值范围,如线性回归的截距设置以及决策树回归器的最大深度、最小分割样本数和最小叶子样本数等。
param\_distributions = {'LinearRegression': {'regressor\_\_fit\_intercept': \[True, False\],},'DecisionTreeRegressor': {'regressor\_\_max\_depth': \[None\] + list(np.arange(1, 21)),'regressor\_\_min\_samples\_split': np.arange(2, 21),'regressor\_\_min\_samples_leaf': np.arange(1, 21)},使用 RandomizeSearchCV 进行超参数优化
将数据集划分为训练集和测试集,对于不同的模型进行超参数优化,记录每个模型的最佳模型、最佳参数和最佳得分。
best\_models = dict()best\_params = dict()best\_score = dict()X\_train, X\_test, y\_train, y\_test = train\_test\_split(X.values, y.values, train\_size=.8)for model in param_distributions.keys():模型性能评估与可视化
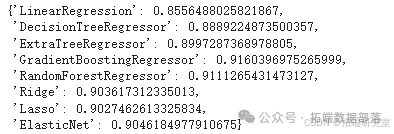
(一)绘制模型性能图
通过比较不同模型的性能,可以看出 “GradientBoostingRegressor”(梯度提升回归器)具有最佳性能。
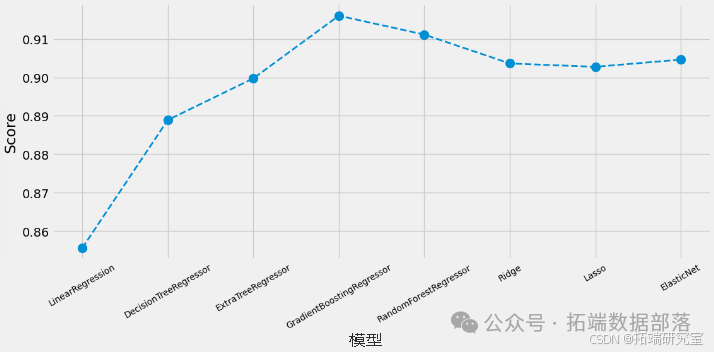
(二)绘制预测结果与真实目标变量的散点图
以 “GradientBoostingRegressor” 模型为例,使用最佳模型对测试集进行预测,然后绘制预测结果与真实目标变量的散点图,以直观地展示模型的预测效果。
model = 'GradientBoostingRegressor'y\_pred = best\_models\[model\].predict(X\_test)# y\_pred = pipeline.predict(X_test)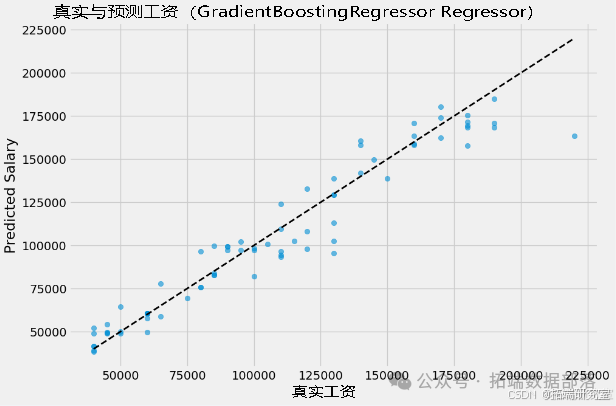
总结
尽管命运或许在某种程度上被决定了,但我们仍然可以通过自己的努力和持续学习来改变自己的命运。在大数据的助力下,我们有望更加精准地预测和解释个人收入的差异,为每个人创造更加公平和美好的未来。
关于分析师

在此对 Greata Xie 对本文所作的贡献表示诚挚感谢,她在悉尼大学完成了金融、商业分析专业的硕士学位,专注数据采集、清洗、可视化和分析等领域。擅长 Python、SQL。
数据获取
在公众号后台回复“收入数据”,可免费获取完整数据。

本文中分析的数据、代码分享到会员群,扫描下面二维码即可加群!
资料获取
在公众号后台回复“领资料”,可免费获取数据分析、机器学习、深度学习等学习资料。

点击文末“阅读原文”
获取全文完整代码数据资料。
本文选自《Python个人收入影响因素模型构建:回归、决策树、梯度提升、岭回归》。
点击标题查阅往期内容
R语言逻辑回归、Naive Bayes贝叶斯、决策树、随机森林算法预测心脏病
PYTHON银行机器学习:回归、随机森林、KNN近邻、决策树、高斯朴素贝叶斯、支持向量机SVM分析营销活动数据|数据分享
PYTHON用户流失数据挖掘:建立逻辑回归、XGBOOST、随机森林、决策树、支持向量机、朴素贝叶斯和KMEANS聚类用户画像
MATLAB随机森林优化贝叶斯预测分析汽车燃油经济性
R语言中贝叶斯网络(BN)、动态贝叶斯网络、线性模型分析错颌畸形数据
使用贝叶斯层次模型进行空间数据分析
MCMC的rstan贝叶斯回归模型和标准线性回归模型比较
python贝叶斯随机过程:马尔可夫链Markov-Chain,MC和Metropolis-Hastings,MH采样算法可视化
Python贝叶斯推断Metropolis-Hastings(M-H)MCMC采样算法的实现
matlab贝叶斯隐马尔可夫hmm模型实现
贝叶斯线性回归和多元线性回归构建工资预测模型
Metropolis Hastings采样和贝叶斯泊松回归Poisson模型
贝叶斯分位数回归、lasso和自适应lasso贝叶斯分位数回归分析免疫球蛋白、前列腺癌数据
R语言RSTAN MCMC:NUTS采样算法用LASSO 构建贝叶斯线性回归模型分析职业声望数据
R语言STAN贝叶斯线性回归模型分析气候变化影响北半球海冰范围和可视化检查模型收敛性
PYTHON用户流失数据挖掘:建立逻辑回归、XGBOOST、随机森林、决策树、支持向量机、朴素贝叶斯和KMEANS聚类用户画像
贝叶斯分位数回归、lasso和自适应lasso贝叶斯分位数回归分析免疫球蛋白、前列腺癌数据
R语言JAGS贝叶斯回归模型分析博士生延期毕业完成论文时间
R语言Metropolis Hastings采样和贝叶斯泊松回归Poisson模型
Python决策树、随机森林、朴素贝叶斯、KNN(K-最近邻居)分类分析银行拉新活动挖掘潜在贷款客户
R语言贝叶斯MCMC:用rstan建立线性回归模型分析汽车数据和可视化诊断
R语言贝叶斯MCMC:GLM逻辑回归、Rstan线性回归、Metropolis Hastings与Gibbs采样算法实例
R语言贝叶斯Poisson泊松-正态分布模型分析职业足球比赛进球数
随机森林优化贝叶斯预测分析汽车燃油经济性
R语言逻辑回归、Naive Bayes贝叶斯、决策树、随机森林算法预测心脏病
R语言用Rcpp加速Metropolis-Hastings抽样估计贝叶斯逻辑回归模型的参数
R语言中的block Gibbs吉布斯采样贝叶斯多元线性回归
Python贝叶斯回归分析住房负担能力数据集
R语言实现贝叶斯分位数回归、lasso和自适应lasso贝叶斯分位数回归分析
Python用PyMC3实现贝叶斯线性回归模型
R语言用WinBUGS 软件对学术能力测验建立层次(分层)贝叶斯模型
R语言Gibbs抽样的贝叶斯简单线性回归仿真分析
R语言和STAN,JAGS:用RSTAN,RJAG建立贝叶斯多元线性回归预测选举数据
R语言基于copula的贝叶斯分层混合模型的诊断准确性研究
R语言贝叶斯线性回归和多元线性回归构建工资预测模型
R语言贝叶斯推断与MCMC:实现Metropolis-Hastings 采样算法示例
R语言stan进行基于贝叶斯推断的回归模型
R语言中RStan贝叶斯层次模型分析示例
R语言使用Metropolis-Hastings采样算法自适应贝叶斯估计与可视化
R语言随机搜索变量选择SSVS估计贝叶斯向量自回归(BVAR)模型
WinBUGS对多元随机波动率模型:贝叶斯估计与模型比较
R语言实现MCMC中的Metropolis–Hastings算法与吉布斯采样
R语言贝叶斯推断与MCMC:实现Metropolis-Hastings 采样算法示例
R语言使用Metropolis-Hastings采样算法自适应贝叶斯估计与可视化
视频:R语言中的Stan概率编程MCMC采样的贝叶斯模型
R语言MCMC:Metropolis-Hastings采样用于回归的贝叶斯估计



![]()