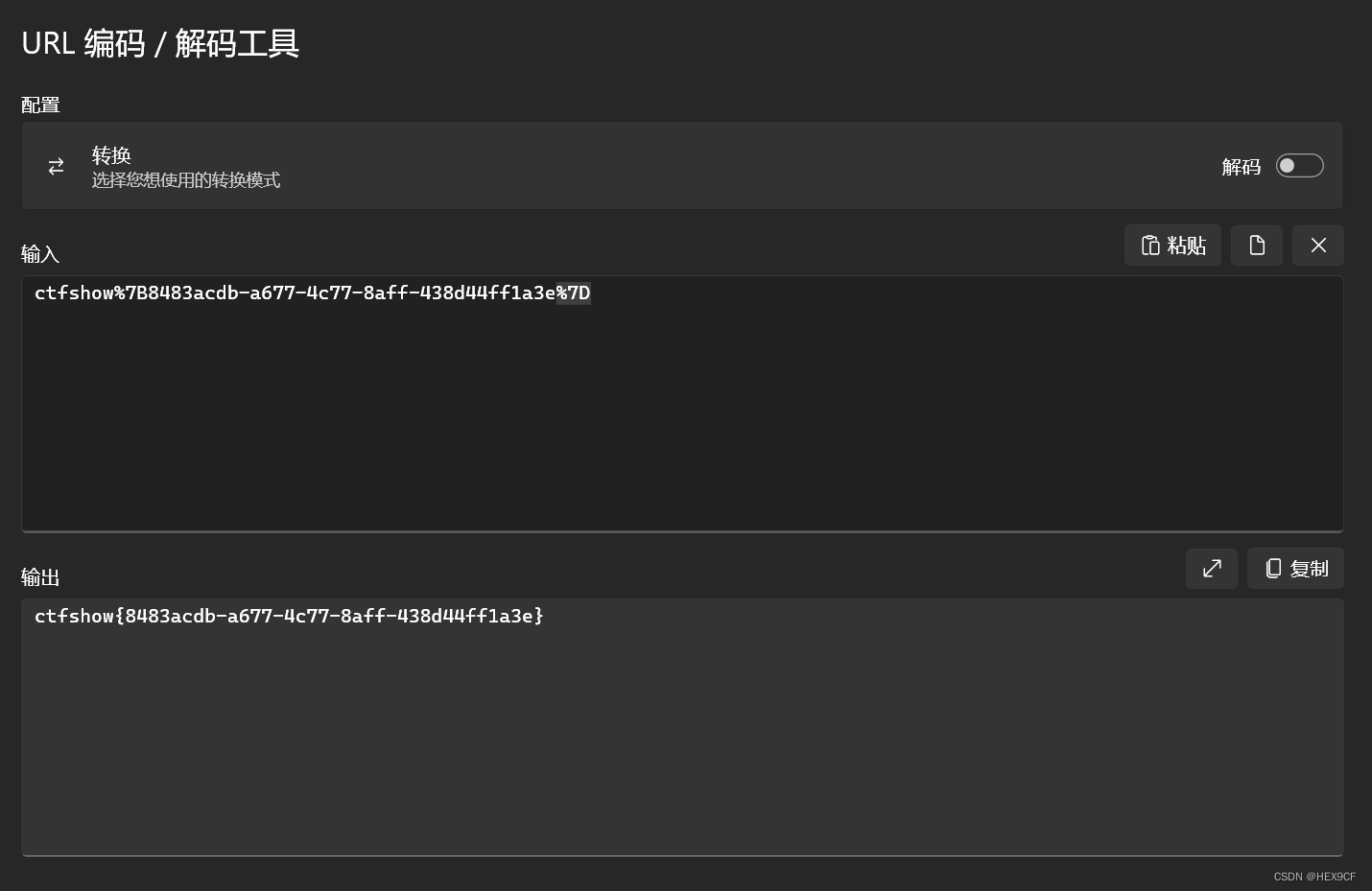
### 思路
1. **建图**：将订单视为图的节点，已知关系视为图的边，构建无向图。
2. **连通分量**：使用深度优先搜索（DFS）或广度优先搜索（BFS）找到图中的所有连通分量。
3. **排序**：对每个连通分量中的订单编号进行排序。
4. **输出**：按最小订单编号的顺序输出每个连通分量。

### 伪代码
1. 读取输入的订单数量n和关系数量m。
2. 构建图的邻接表表示。
3. 使用DFS/BFS找到所有连通分量。
4. 对每个连通分量中的订单编号进行排序。
5. 按最小订单编号的顺序输出每个连通分量。

### C++代码

#include <iostream>
#include <vector>
#include <algorithm>
#include <set>

using namespace std;

void dfs(int node, vector<vector<int>>& graph, vector<bool>& visited, vector<int>& component) {
    visited[node] = true;
    component.push_back(node);
    for (int neighbor : graph[node]) {
        if (!visited[neighbor]) {
            dfs(neighbor, graph, visited, component);
        }
    }
}

int main() {
    int n, m;
    cin >> n >> m;
    vector<vector<int>> graph(n + 1);
    for (int i = 0; i < m; ++i) {
        int a, b;
        cin >> a >> b;
        graph[a].push_back(b);
        graph[b].push_back(a);
    }

    vector<bool> visited(n + 1, false);
    vector<vector<int>> components;

    for (int i = 1; i <= n; ++i) {
        if (!visited[i]) {
            vector<int> component;
            dfs(i, graph, visited, component);
            sort(component.begin(), component.end());
            components.push_back(component);
        }
    }

    sort(components.begin(), components.end(), [](const vector<int>& a, const vector<int>& b) {
        return a[0] < b[0];
    });

    cout << components.size() << endl;
    for (const auto& component : components) {
        for (int order : component) {
            cout << order << " ";
        }
        cout << endl;
    }

    return 0;
}