CTEA论文翻译

Embedding-Based Entity Alignment of Cross-Lingual Temporal Knowledge Graphs

基于嵌入的跨语言时序知识图谱实体对齐

ABSTRACT

实体对齐旨在通过匹配多源知识图谱中的相同实体来构建完整的知识图谱(KG)。现有的实体对齐研究主要集中在知识边缘图中的静态多关系数据。然而，实体之间的关系或属性通常也具有时间特征。忽视这些时间特征经常会导致对齐错误。与研究时序知识图谱中的实体对齐相比，跨语言时序知识图谱中的实体对齐方面的工作相对较少。因此，在本文中，我们提出了一种跨语言时序知识图的实体对齐方法，即CTEA。CTEA在GCN和TransE的基础上，将实体嵌入、关系嵌入和属性嵌入相结合，设计了联合嵌入模型，更有利于生成可迁移的实体嵌入。同时，将元素之间的距离计算和实体对的相似度计算相结合，增强跨语言实体对齐的可靠性。实验表明，与最新方法相比，所提出的CTEA模型将Hits@m和MRR提高了约0.8~2.4个百分点。

1. Introduction

随着智能应用的不断发展，有大量的应用场景需要知识随着时间的推移而更新。然而，现有的知识图谱研究主要集中在传统的静态知识图谱，无法满足知识动态变化的要求。因此，衍生出包含时间信息的知识图，称为时序知识图谱。时序知识图谱是随着时间的推移更新实体以及实体之间的关系的知识图谱，具有较高的时效性。它使得下游任务能够更方便地感知当前时刻的准确知识，因此具有重要的研究意义。时序知识图谱已成为人工智能和自然语言处理领域许多应用的重要基础。如果要构建跨语言应用，实现 DBpedia和 YAGO等跨语言时序知识图处理具有重要意义。由于许多广泛使用的时序知识图之间存在数据交集，不同资源的同时使用可能会导致数据冗余，这给时序知识图的应用带来挑战。因此，实现跨语言时序知识图的实体对齐具有重要意义。受(Ji等人)的启发，时序知识图谱主要分为四个研究领域，包括时序嵌入、实体动态性、时间关系依赖性和时间逻辑推理。本文工作主要集中在时序嵌入领域，通过联合时序嵌入实现跨语言时序知识图谱的实体对齐。

由于时序知识图谱中的实体随着时间不断变化，实体的属性值及其与其他实体的关系也会随着时间而变化。在一些时间敏感的应用场景中，例如金融领域的智能投研、智慧医疗的辅助预测、购物网站的搜索推荐等，需要综合分析实体的属性信息和关系之间的实体以确定不同时序知识图谱中的实体是否对齐。此外，现有的方法经常忽略时间特征，只处理关系，导致像(John Adams, president of, 1797-1801, American)和(John Quincy Adams, president of, 1825-1829, American)这样的实体对齐。然而，解决关系的时间特征可以轻松避免此类问题。跨语言时序知识图谱往往由于不同语言间含义不同、语义环境不同、不同语言使用者的知识背景不同等问题，导致时序知识图谱中知识的描述存在很大差异，使得实现起来极其困难，在跨语言时序知识边缘图上进行知识融合、知识推理和知识查询操作，面临着巨大的挑战。跨语言时序知识图谱的实体对齐任务是找出两个跨语言知识图谱中代表同一现实世界对象的实体。它面临的关键挑战是充分考虑不同语言知识图谱之间的语义相关性和时间顺序特征。此外，目前跨语言知识图谱实体对齐中时间信息形成的研究还处于空白阶段，其时间表示尚未得到研究。现有的工作主要集中在静态知识图谱上，其中事实不随时间变化，而对知识图谱随时间变化的动态特征探索较少。一项调查(Ji等人)可以大致分为传统方法和基于嵌入的方法。传统方法需要通过机器翻译在不同语言之间架起桥梁，这使得跨语言场景中的对齐质量很大程度上依赖于多种语言之间的翻译质量，其准确性并不理想。因此，研究人员设计了基于嵌入学习的跨语言实体对齐方法。这些工作将跨语言知识图谱映射到相同的低维向量空间中，其中等效实体彼此靠近。例如，AKE提出了一种新颖的对抗性知识嵌入框架，该框架利用对抗性学习原理对嵌入分布对齐进行建模。 在该模型中，提出了嵌入分布对齐的新思路，通过正则化未映射实体来保证嵌入空间的近似同构。JAPE 提出了一种用于跨语言实体对齐的联合属性保存嵌入模型，可以将来自不同语言的知识合并到模型中。SEA 是一种半监督实体对齐方法，解决了实体度差异对知识图嵌入的影响问题。MRAEA 可以通过关注节点的传入和传出邻居的元语义及其连接关系来直接对跨语言实体嵌入进行建模。这些基于翻译的方法假设两个跨语言知识图具有相似的结构，因此对齐的实体对的嵌入在向量空间中应该具有相对相似的位置。然而，在实践中，跨语言知识图谱在结构上可能并不相似。同时，上述方法只能处理1对1的关系，无法处理1对n、n对1等复杂关系。

为了解决上述问题，研究人员提出了基于邻域的跨语言知识图谱实体对齐方法，该方法可以通过聚合相邻节点的信息来生成节点级嵌入。Rea是一种基于 GNN 的噪声感知实体对齐方法，它设计了基于对抗训练原理的噪声检测，以解决由于噪声标签而导致的实体对齐问题。KDCoE 提出了一种基于 GNN 的 MuGNN 模型，通过从不同角度对图进行编码来学习面向对齐的嵌入。它还联合执行知识图推理和对齐，从而通过规则推理和转移的完成以及通过跨KG注意力的剪枝来明确地协调知识图的异质性。 还有一些基于GCN的方法，例如Wang等人在跨语言实体对齐中将实体关系和实体属性结合起来，有效提高了实体对齐的结果。 徐等人提出了两种称为 Cross-TextGCN 和 Cross-TextMatch 的文本嵌入模型，以学习实体描述嵌入并促进跨语言实体对齐。杨等人基于 GCN 设计 MAN 和 HMAN，将多方面特征融入到跨语言实体嵌入中，然后结合基于 GCN 的模块和基于 BERT 模型的模块进行跨语言知识图对齐 。虽然基于GCN的跨语言实体对齐模型产生了很好的对齐效果，但不幸的是，上述方法仅从实体邻域的角度执行跨语言实体。这种单一嵌入学习会导致产生有限数量的实体嵌入，并限制实体对齐的性能。

因此，研究人员针对该问题提出了基于GCN的改进的跨语言实体对齐模型。AliNet在模型中引入远邻域来扩大邻域结构之间的覆盖范围，同时采用注意力机制来减少噪声，从而导致实体对齐的大幅增加。KE-GCN提供了现有高级 GCN 模型的统一视图。它基于GCN更新实体和关系嵌入，并基于这两个嵌入实现递归聚合过程。JEANS结合了 GCN 和 TransE 来学习实体嵌入，利用基础过程来学习文本嵌入，并设计了一个附带监督模型。该模型可以通过对齐学习过程以自学习的方式捕获实体和词位的跨语言对应关系。通过建立文本语料库，与知识图谱中的文本信息关联起来，可以监督实体对齐过程。它可以解决现有的基于种子对齐的问题。尽管上述方法各有优点，但不幸的是，存在三个不足：1)单独使用 GCN 或 TransE 的嵌入学习限制了可以生成的实体嵌入的数量。 原因是GCN将不同语言的实体嵌入到同一个向量空间中，需要配合预定义的距离函数作为度量。传统的跨语言实体对齐方法依赖于机器翻译，其准确性还远未达到完美。TransE适合处理不同类型实体之间的一对一关系。2)仅通过邻域的距离计算或实体向量的相似度计算来判断对齐实体，实体对齐结果不够可靠。3)没有考虑时间数据的处理，因此此类方法不适用于时序知识图谱。

跨语言时序知识图谱实体对齐的目的是结合时间特征，将不同语言的知识图谱中语义相似的实体关联起来，解决知识图谱融合等更深层次的问题。针对现有实体对齐的不足，跨语言时序知识图谱的实体对齐方法有待进一步研究。GCN 可以将两个时序知识图谱的实体嵌入到统一的向量空间中。与 GCN 相比，TransE 在处理稀疏结构的时序知识图方面更加鲁棒。因此，CTEA选择结合GCN和TransE来学习跨语言时序知识图的实体嵌入，为跨语言时序知识图实体对齐任务的实现奠定基础，本文的主要贡献如下：

• 基于GCN和TransE，我们提出了一种跨语言时序知识图谱的实体对齐方法，即CTEA。CTEA结合了实体嵌入、关系嵌入和属性嵌入，考虑了时间信息对关系和属性的影响，设计了联合嵌入学习模型，更有利于生成可迁移的实体嵌入。
• 将元素之间的距离计算和实体对的相似度计算相结合，增强跨语言实体对齐的可靠性。
• 在 DBpedia (English&French) 和 DBpedia (English&German) 数据集上进行了实验。与基线相比，所提出的 CTEA 模型在 Hits@m 和 MRR 上的表现优于最先进的模型。

2. Related Works

2.1. Translation-based cross-lingual entity alignment

有一些基于翻译的跨语言实体对齐模型，将分离的知识图编码到不同的低维嵌入空间中。翻译模型包括 TransE、TransR、PTransE、DistMult、RotatE、RotatE、QuatE等。其中，通常利用TransE或其扩展来获取每个知识图谱中的实体嵌入和关系嵌入，然后通过联合学习将这些嵌入映射到统一的向量空间。例如，AKE提出了一种嵌入分布对齐的新思想，通过正则化未映射的实体来确保嵌入空间的近似同构。为了实现上述目标，研究人员提出了一种新颖的对抗性知识嵌入框架。 该框架包含三个模块。主要思想是利用对抗性学习的原理对嵌入分布对齐进行建模。 例如，JAPE设计了一种用于跨语言实体对齐的联合属性保存嵌入模型，它可以将不同语言的知识合并到模型中。图结构被映射到相同的嵌入空间，然后使用相关属性进行细化。BootEA引入了知识图嵌入模型来学习跨不同知识图的面向对齐的嵌入，并在引导过程中进行实体对齐。除了使用关系三元组之外，一些方法还引入了实体的其他特征。例如，MTransE将实体和关系分别嵌入到每个知识图中，然后共同学习不同语言特定嵌入空间之间的跨语言转换。JAPE和 AttrE 使用属性信息来改进实体嵌入。SEA 是一种半监督实体对齐方法，解决了实体度差异对知识图嵌入的影响问题。MRAEA可以通过关注节点的传入和传出邻居的元语义及其连接关系来直接对跨语言实体嵌入进行建模。还有一些研究人员通过基于翻译的方法对异构知识图中的实体进行编码，并通过底层拓扑结构做出不同的对齐假设。此外，大多数实体对齐方法都是针对单语知识图谱研究，如IPTransE、MultiKE、OTEA、COTSAE、IMUSE等。他们可以为这项研究提供一些想法。然而，基于翻译模型的跨语言时序知识图实体对齐的研究相对较少，并且存在一些基于翻译的单语时序知识图实体对齐模型。例如，ARIM-TE通过内部规律性和外部影响力对元素级信息进行建模。引入合并门，通过将包括局部和全局效应在内的内部规律与外部随机扰动相结合来对事实级信息进行建模。 最后，根据获得的丰富特征的多粒度信息，在结构和语义上进行对齐。

2.2. GCN-based cross-lingual entity alignment

最近，研究人员利用图卷积网络设计了跨语言实体对齐方法，该方法更加关注实体的邻域信息。在(Wang et al.，2018)中，知识图谱中的每个实体关系都被用来构建图卷积神经网络结构，并且在模型训练中仅考虑实体之间的等价关系。该方法只需要知识图谱之间少量预对齐的跨语言实体作为训练数据，不需要任何预对齐的关系或属性，模型复杂度较小。同时，实体关系和实体属性可以有效结合，有效提高实体对齐的结果。STGCN重点研究如何在跨语言实体对齐任务中利用每个实体的描述。在不同语言的知识图谱之间构建跨语言的文本图谱，然后通过单词和实体在知识图谱之间传递语义特征，并基于GCN对实体进行编码。接下来，使用预训练的跨语言对齐词嵌入对实体描述进行编码，从而训练跨语言实体对齐模型。在(Yang et al., 2019)中，利用知识图谱的各个方面设计了一种跨语言实体嵌入学习的新方法。它提出了两种基于GCN的模型变体，即MAN和HMAN，它们将多方面的特征融入到跨语言实体嵌入中，主要包括拓扑特征、关系类型和属性。为了捕获文本描述之间的语义相关性，它对预训练的多语言 BERT 模型进行了微调，以弥合不同语言之间的差距。最后，该模型结合了基于 GCN 的模块和基于 BERT 模型的模块，用于跨语言知识图谱对齐。NAEA将知识图谱中的邻居级和关系级特征信息结合起来执行多语言实体对齐任务，可以更好地捕获实体和关系特征以定位对齐实体。SDEA 使用预训练的基于 Transformer 的语言模型从属性值中捕获语义信息，关系嵌入使用具有注意力机制的 GRU 模型。通过选择性地聚合来自邻居的语义信息，提出了一种用于有效实体对齐的语义驱动实体嵌入方法。还有一些基于 GCN 的实体对齐方法专注于单语言知识图，例如 RDGCN 和 HGCN。另外，上述与知识图谱相关的实体对齐方法都有各自的优点。不幸的是，它们都不适用于时序知识图谱。跨语言时序知识图实体对齐的研究很少涉及，而基于GCN的单语言时序知识图实体对齐已有学者研究。因为传统的知识图谱实体对齐方法无法处理包含时间信息的复杂对象。 为了解决这个问题，TEA-GNN首次提出了时序知识图谱之间实体对齐的 GNN，将实体、关系和时间戳嵌入到向量空间中，并使用 GNN 来学习实体 表示。利用时间感知注意力机制将关系和时间信息结合到GNN结构中，为不同节点分配不同的权重，并利用正交变换矩阵计算邻域中相关性和时间戳的嵌入。Tem-EA使用循环神经网络来学习时间序列表示，并使用图卷积网络和基于平移的嵌入模型来学习结构信息和属性信息。TREA将实体、关系和时间戳映射到嵌入空间中，使用图神经网络(GNN)捕获图中的信息，并使用时间关系注意力集成节点之间的关系和链接的时间特征 机制。STEA提出了一种简单的图神经网络模型，结合时间信息匹配机制，以更少的时间和更少的参数获得更好的性能。此外，还提出了一种通过选择最近邻来生成对齐种子的简单策略，该策略通过时间信息生成无监督对齐种子。

3. Entity alignment between cross-lingual temporal knowledge graphs

3.1. Problem formulation

为了完成跨语言时序知识图之间的实体对齐任务，本节定义了跨语言时序知识图实体对齐的问题表述。下面介绍时序知识图的建模方法。

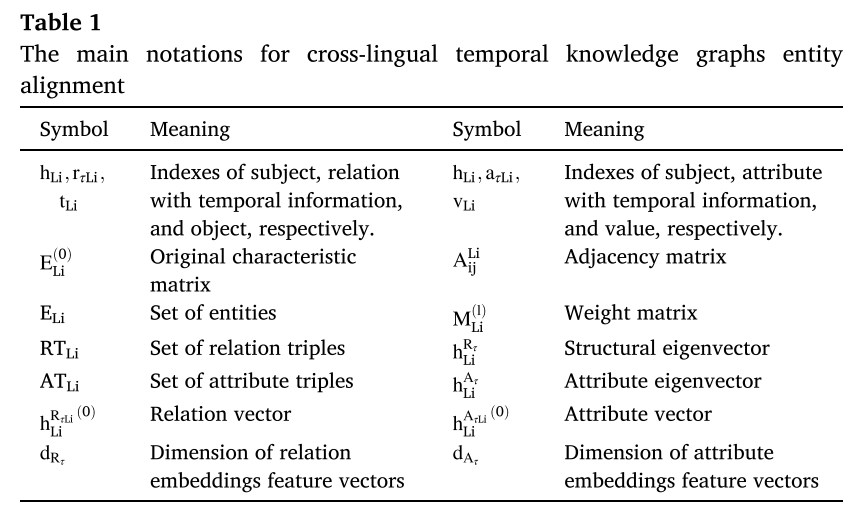
给定语言集合 L = { L 1 , L 2 , L 3 , . . . , L i , . . . , L m − 1 , L m } , ( m = ∥ L ∥ ) L=\{L_{1}, L_{2}, L_{3}, ..., L_{i}, ..., L_{m-1}, L_{m}\}, \mathrm{(m}=\parallel L\parallel) L={L1​,L2​,L3​,...,Li​,...,Lm−1​,Lm​},(m=∥L∥)，其中 $L_i$ 描述 $L$ 中的某种语言，$m$ 的值是语言的数量。跨语言时序知识图谱的符号形式可以表示为 ${\mathrm{G}}_{\mathrm{Li}}=({\mathrm{E}}_{\mathrm{Li}},\mathrm{R}{\mathrm{T}}_{\mathrm{Li}},\mathrm{A}{\mathrm{T}}_{\mathrm{Li}}),\mathrm{i}\le \mathrm{m}\cap \mathrm{Li}\in \mathrm{L}$，其中 $G_{Li}$ 表示语言 $L_i$ 的时序知识图谱，$L$ 表示所有语言的时序知识图谱的集合。$E_{Li},R{T}_{Li},A{T}_{Li}$分别表示语言$L_i$时序知识图谱的实体集、包含时态信息的关系三元组和包含时态信息的属性三元组。跨语言时序知识图实体对齐的定义如定义1所示。在定义之前，我们首先声明本文使用的相关符号，如表1所示。

定义1. (跨语言时序知识图谱实体对齐) 给定使用语言 $L_1$ 的时序知识图谱 $G_{L1}=(E_{L1},R{T}_{L1},A{T}_{L1})$ 和使用语言$L_2$$G_{L2}=(E_{L2},R{T}_{L2},A{T}_{L2})$，当 i ∈ { 1 , 2 } i \in \{1,2\} i∈{1,2} 时， E L 1 = { e 1 L 1 , e 2 L 1 , . . . , e ∣ E L 1 ∣ L 1 } , E L 2 = { e 1 L 2 , e 2 L 2 , . . . , e ∣ E L 2 ∣ L 2 } , R T L 1 ∣ R T L 2 E_{L1} = \{e_{1}^{\mathrm{L1}}, e_{2}^{\mathrm{L1}}, ..., e_{|E_{L1}|}^{\mathrm{L1}}\}, E_{L2} = \{e_{1}^{\mathrm{L2}}, e_{2}^{\mathrm{L2}}, ..., e_{|E_{L2}|}^{\mathrm{L2}}\},RT_{L1}|RT_{L2} EL1​={e1L1​,e2L1​,...,e∣EL1​∣L1​},EL2​={e1L2​,e2L2​,...,e∣EL2​∣L2​},RTL1​∣RTL2​ 和 $A{T}_{L1}|A{T}_{L2}$ 由 $(h_{L1},r_{\tau L1},t_{L1})$ 和 $(h_{L2},r_{\tau L2},t_{L2})$ 分别包含作为 TA-TransE 的时间信息。跨语言时序知识图谱之间的实体对齐任务旨在找到每个实体对 { e m L 1 , e n L 2 ) ∣ m ∈ [ 1 , ∣ E L 1 ∣ ] , n ∈ [ 1 , ∣ E L 2 ∣ ] , e m L 1 ∈ ∣ E L 1 ∣ , e n L 2 ∈ ∣ E L 2 ∣ } \{e_m^{\mathrm{L}1},e_n^{\mathrm{L}2})\mid m\in[1, |E_{L1}|], n\in[1, |E_{L2}|], e_m^{\mathrm{L}1} \in |E_{L1}|, e_n^{\mathrm{L}2} \in |E_{L2}|\} {emL1​,enL2​)∣m∈[1,∣EL1​∣],n∈[1,∣EL2​∣],emL1​∈∣EL1​∣,enL2​∈∣EL2​∣}，其中 $e_m^{\mathrm{L}1}$ 和 $e_n^{\mathrm{L}2}$ 表示使用相同的现实世界实体不同的语言。

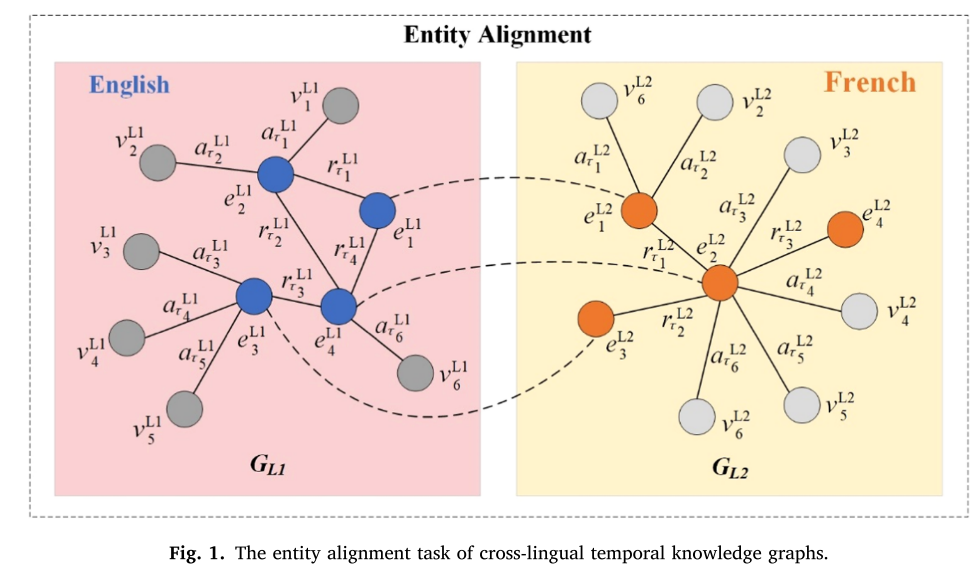
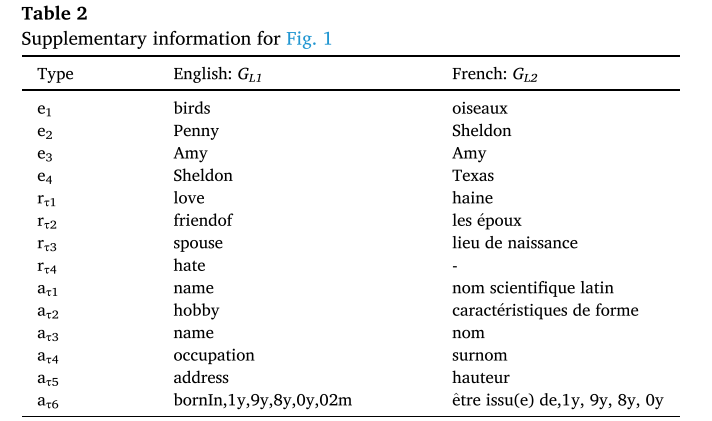
如图1所示，通过一个示例详细说明跨语言时序知识图谱实体对齐。在图1中，时序知识图谱$G_{L1}$的语言是英语，并且时序知识图谱$G_{L2}$的语言是法语。根据实体对齐规则，在$G_{L1}$和$G_{L2}$中找到表示真实的世界中的相同实体的实体对。为了区分实体和文本(实体关系和实体属性的描述)，$G_{L1}$和$G_{L2}$中分别使用不同的颜色来表示实体和文本。图1中的数据均为真实的世界中的真实的数据，表2对图1中的时序知识图谱中的内容进行了补充，表2示出了时序知识图$G_{L1}$和时序知识图$G_{L2}$中的实体、关系和属性的对应信息。$G_{L1}$和$G_{L2}$中的属性$a\tau 6$具有时间信息，其分别为“bornIn, 1y, 9y, 8y, 0y, 02m”和“ˆe tre issu (e) de, 1y, 9y, 8y, 0y”。时序知识图谱的实体对齐反映在实体属性值和关系的变化上。例如，一个人可能会搬到另一个城市居住或换到新的学校，然后新的属性也可以添加到实体。因此，如果关系和属性的一致性存在差异，则会影响实体对齐的结果。

3.2. Overview

3.1节形式化了跨语言时序知识图谱的实体对齐任务。下面将详细介绍跨语言时序知识图的实体对齐方法。为了解决跨语言时序知识图谱的实体对齐问题，本节提出了一种知识图实体对齐方法：CTEA。该模型主要分为三个部分，如图2所示，其中使用的符号如表1所示。给定两个跨语言时序知识图$G_{L1}=(E_{L1},R{T}_{L1},A{T}_{L1})$和$G_{L2}=(E_{L2},R{T}_{L2},A{T}_{L2})$，CTEA模型的框架如图2所示。该模型主要分为两部分：嵌入学习模块和实体对齐模块。

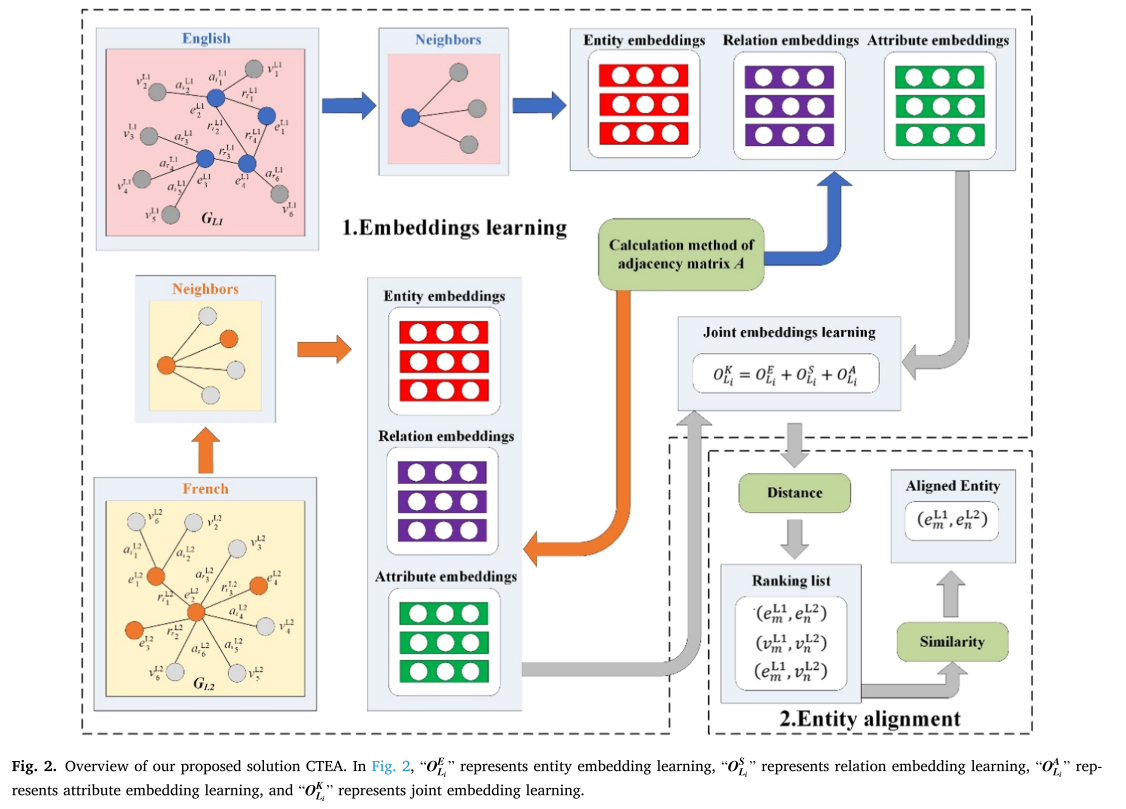
在嵌入学习模块中，分别提出了实体嵌入学习、关系和属性嵌入学习以及联合嵌入学习。输入是两个时序知识图谱，其中时序知识图谱$G_{L1}$的语言是英语，时序知识图谱$G_{L2}$的语言是法语。时间信息以时间标记的形式添加到谓词中。我们将谓词 $p$ 和时间标记 $\tau$(如果存在时间信息)之间的连接称为谓词序列 $p_{\tau }$。 当$p_{\tau }$表示头实体 $h$ 和尾实体 $t$ 之间的关系时，这里 $p_{\tau }$ 被称为关系$r_{\tau }$。当$p_{\tau }$表示头实体 $h$ 和尾实体 $t$ 之间的属性时，这里 $p_{\tau }$ 被称为属性$a_{\tau }$。谓词序列可以包含时间信息，或者可以不包含时间信息。在实体嵌入学习中，首先使用GCN从图结构的角度获取信息，将两个知识边缘图的实体嵌入到统一的向量空间中。然后使用 TransE 生成可转移实体嵌入。在关系和属性嵌入学习中，GCN 用于分别从关系三元组和属性三元组中学习和嵌入信息。由于传统GCN中不区分不同关系的重要性，因此确定通过不同关系连接到对齐实体的两个实体具有相同的等效概率。这里提出一种邻接矩阵的计算方法来解决这个问题。在联合嵌入学习中，实体嵌入、关系嵌入和属性嵌入相结合，经过优化后产生最终的嵌入结果。在实体对齐模块中，时序知识图谱中的元素在向量空间中的距离越小，相似度就越高，从而使得对齐的可能性越高。因此，通过计算实体的邻域距离，得到一个从小到大排序的列表$RL$。该列表包括$G_{L1}$中的任意实体$e_m^{\mathrm{L}1}$与其邻居以及$G_{L2}$中的所有实体及其邻居之间的距离，因此该列表可以用作实体对齐的候选集。然后，通过相似度计算，当$Sim(e_m^{L1},e_n^{L2})>{\theta }_E$时，可以认为两个实体是相似实体对。$G_{L2}$ 到 $G_{L1}$ 的对齐也是如此。因此，将邻域距离计算与向量相似度计算相结合，使得实体对齐的结果更加可靠。

3.3. Embeddings Learning

Embeddings学习模块负责将跨语言时序知识图的关系和实体嵌入到低维向量空间中，并从知识图结构和实体属性两个方面收集证据，即实体嵌入、关系嵌入和属性嵌入。为了完成跨语言时序知识图的嵌入学习，假设：1)等价实体具有相似的属性； 2)等效实体通常与其他等效实体相邻。

3.3.1. Entity Embeddings Learning

GCN模型已被证明可以有效地获得实体嵌入。然而，在稀疏知识图谱中，TransE方法表现出更强的鲁棒性。因此，我们设计了一种新颖的嵌入方法，成功地结合了两种方法的优点。

前人在跨语言时序知识图实体对齐中使用的嵌入方法可以分为两种形式：关系嵌入和邻域嵌入。关系嵌入主要基于翻译模型TransE等，利用关系生成实体嵌入，例如JAPE。邻域嵌入利用由大量实体之间的关系组成的子图结构，主要基于图神经网络(GNN)或图卷积网络(GCN)。它可以从图结构(例如依赖图)捕获信息，例如 HMAN。由于实体的关系和邻近度都有利于可转移实体嵌入的生成，因此我们在这项工作中结合了这两种嵌入技术。

GCN可以将两个知识图的实体嵌入到统一的向量空间中，非常适合建模跨语言的时序知识图结构。最近，GCN 已被用于基于嵌入的实体对齐。为了达到结合两种嵌入技术的目标，模型中首先训练n层GCN。将跨语言时序知识图$G_{L1}$和$G_{L2}$构造成邻接矩阵$A_{ij}^{L1}$和$A_{ij}^{L2}$，$|E_{L1}|\times |E_{L1}|$和$|E_{L2}|\times |E_{L2}|$，其中 $A_{ij}$ 是根据 $e_i\in E_{Li}$ 和 $e_j\in E_{Lj}$ 的相关信息计算得到的对称邻接矩阵(即 $A_{ij}=\frac{A_{ij}}{\sqrt{d_i}\sqrt{d_j}}$ )，简单地用式(1)中的 A 表示。$E_{Li}^{(0)}$用于表示原始特征矩阵，其中每一行对应一个实体，原始特征矩阵可以是实体属性，也可以是随机初始化的。GCN由多个图卷积层组成，用$E_{Li}^{(l)}\in R^{n\times d(l)}$表示第$l$层的实体嵌入，则第$l+1$层的实体嵌入，$E_{Li}^{(l+1)}$可由式(1)计算。

$$E_{Li}^{(l+1)}=\sigma \left({\hat{D}}^{-\frac{1}{2}}\hat{A}{\hat{D}}^{-\frac{1}{2}}{E}_{Li}^{(l)}{M}_{Li}^{(l)}\right)(1)$$

其中，$\hat{A}=A+L$，$A$是$|E_{Li}|\times |E_{Li}|$邻接矩阵表示图的结构信息，$L$是单位矩阵，$\hat{D}$是$\hat{A}$的度矩阵，${\hat{D}}^{-\frac{1}{2}}\hat{A}{\hat{D}}^{-\frac{1}{2}}$对$A$进行对称归一化变换。$M_{Li}^{(l)}\in R^{d(l)\times d(l+1)}$描述了一个可学习的权重矩阵，它可以用于${\hat{D}}^{-\frac{1}{2}}\hat{A}{\hat{D}}^{-\frac{1}{2}}{E}_{Li}^{(l)}$的线性变换。激活函数$\sigma (\ast )$可以由$ReLU(\ast )=max(0,\ast )$得到，它可以对${\hat{D}}^{-\frac{1}{2}}\hat{A}{\hat{D}}^{-\frac{1}{2}}{E}_{Li}^{(l)}{M}^{(l)}$进行非线性变换，得到 $l+1$层的输出$E_{Li}^{(l+1)}$。

最后一层GCN输出的嵌入表示$E^{(l+1)}$作为关系嵌入学习的输入。由于时序知识图通常是稀疏的，因此当结构稀疏时，翻译模型更健壮。因此，本节选择了翻译模型TransE来建模这些关系，为实现跨语言时序知识图实体对齐任务奠定了基础。能量函数如式(2)所示。在这一部分中，关系三元组$R{T}_{Li}=(h_{Li},r_{\tau Li},t_{Li})$被用于在$L_i$语言的嵌入空间中的关系建模，并且$E_{Li}$被用作$L_i$语言的实体表示。公式(2)用于所涉及的每种语言，并且优化的log-softmax损失函数如公式(3)所示。

$$f_{Li}(h,r_{\tau },t)=\parallel {\mathbf{h}}_{Li}+{\mathbf{r}}_{\tau Li}-{\mathbf{t}}_{Li}\parallel (2)$$

$$O_{L_i}^E=-\sum _{T_{Li}\in G_{Li}}log\frac{exp(\beta -f_{Li}(T_{Li}))}{{\sum }_{T_{Li}\notin G_{Li}}exp\left(\beta -f\left(T_{Li}^{{}^{\prime }}\right)\right)}(3)$$

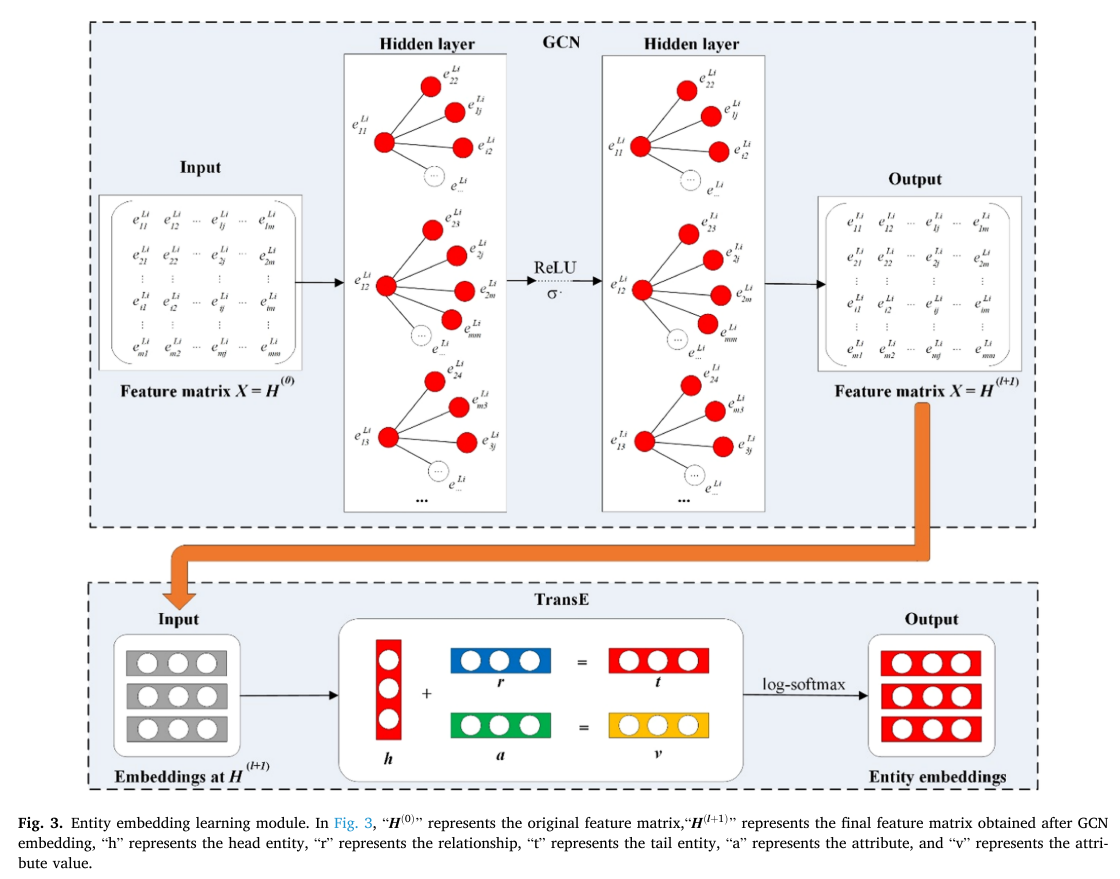
其中$f_{Li}(T_{Li})$是关系三元组$R{T}_{Li}$的可能性度量，它使用粗体首字母表示向量。$O_{L_i}^E$表示实体嵌入学习的log-softmax损失函数，其中所有实体都来自$E_{Li}$。$\beta$表示正偏差，用来调整可能性测度的尺度。在公式(4)中，$T_{Li}^{{}^{\prime }}$表示负采样关系三元组。实体嵌入学习模块的具体内容如图3所示。

$$T_{Li}=\{(h_{Li},r_{\tau Li},t_{Li})\in G_{Li}\};T_{Li}^{{}^{\prime }}=\left\{\left(h_{Li}^{{}^{\prime }},r_{\tau Li},t_{Li}\right)|h_{Li}^{{}^{\prime }}\in E_{Li}\right\}\cup \left\{\left(h_{Li},r_{\tau Li},t_{Li}^{{}^{\prime }}\right)|t_{Li}^{{}^{\prime }}\in E_{Li}\right\}(4)$$

3.3.2. Relation and Attribute Embeddings Learning

在跨语言时序知识图$G_{L1}$和$G_{L2}(i=1,2)$中，关系由$R_{\tau Li}$表示，属性由$A_{\tau Li}$表示。该模块使用GCN模型学习关系嵌入和属性嵌入，并为GCN层中的每个实体分配两个特征向量：关系特征向量$h_{Li}^{R_{\tau }}$和属性特征向量$h_{Li}^{A_{\tau }}$。在输入层，用$E_{Li}^{R_{\tau Li}}$和$E_{Li}^{A_{\tau Li}}$表示$Li$语言时序知识图中所有实体的原始关系特征矩阵和原始属性特征矩阵。$h_{Li}^{R_{iL{i}^{(0)}}}$用于表示随机初始化并随训练过程不断更新的关系向量。$h_{Li}^{A_{iLi}(0)}$表示实体的属性向量，其在模型训练期间是固定的。如果$E_{Li}^{R_{\tau }Li(l)}$表示在水平$l$处的关系嵌入，则在水平$l+1$处的关系嵌入的$M_{Li}^{R_{\tau Li}(l+1)}$可以由公式(5)计算。

$$E_{Li}^{R_{\tau Li}(l+1)}=\sigma \left({\hat{D}}^{-\frac{1}{2}}\hat{A}{\hat{D}}^{-\frac{1}{2}}{E}_{Li}^{R_{\tau Li}(l)}{M}_{Li}^{R_{\tau Li}(l)}\right)(5)$$

其中$A$是$|E_{Li}|\times |E_{Li}|$表示图的结构信息的邻接矩阵。$\hat{A}=A+L$，$L$表示单位矩阵。$\hat{D}$表示$\hat{A}$的度矩阵。$M_{Li}^{R_{\tau Li}(l)}$表示关系在$l$层的权矩阵。$\sigma (\ast )$是非线性激活函数$ReLU(\ast )=max(0,\ast )$。

类似地，$l+1$层的属性嵌入$E_{Li}^{A_{\tau Li}(l+1)}$可以由公式(6)计算，其中$M_{Li}^{A_{\tau Li}(l)}$表示在$l+1$层的属性的权重矩阵。

$$E_{Li}^{A_{\tau Li}(l+1)}=\sigma \left({\hat{D}}^{-\frac{1}{2}}\hat{A}{\hat{D}}^{-\frac{1}{2}}{E}_{Li}^{A_{\tau Li}(l)}{M}_{Li}^{A_{\tau Li}(l)}\right)(6)$$

邻域信息对于知识图的结构表示非常重要，因为相似的实体通常具有相似的邻域子图。然而，两个实体同时通过不同的关系(如朋友、配偶)连接到对齐的实体，它们的等价概率并不相同，这在传统的GCN模型中是无法区分的。因此，公式(7)给出了用于计算关系和属性的相邻矩阵( A i j L i ∈ A , L i = { L 1 , L 2 } A_{ij}^{Li}\in A, Li = \{L1, L2\} AijLi​∈A,Li={L1,L2})的方法。然后，公式(5)中的邻接矩阵A可以通过公式(7)中的$A_{ij}^{Li}(R{T}_{Li})$来计算。

$$A_{ij}^{Li}(R{T}_{Li})=\sum _{R{T}_{Li}\in G_{Li}}\frac{num(tail)\cdot num(r_{\tau })}{num{\left(r_{ij}^{Li}\right)}^2}+\sum _{R{T}_{Li}\in G_{Li}}\frac{num(head)\cdot num(r_{\tau })}{num{\left(r_{ji}^{Li}\right)}^2}(7)$$

其中$r_{ij}^{Li}$表示从实体$i$到实体$j$的关系，并且$r_{ji}^{Li}$表示从实体$j$到实体$i$的关系。$num(head)$是关系的头实体的数量，$num(tail)$是关系的尾实体的数量，并且$num(r_{ij}^{Li})$是关系$r_{ij}^{Li}$的数量。

式(6)中的邻接矩阵$A$可以通过式(8)中的$A_{ij}^{Li}(A{T}_{Li})$计算，其中$a_{ij}^{Li}$表示实体$i$和属性值$j$之间的属性，$num(head)$为属性布特的头部实体的数目，$num(tail)$表示属性的尾部实体的数目其中，$num(a_{\tau })$表示包含时间信息的属性的数量(即属性值)，$num(a_{ij}^{Li})$是属性$a_{ij}^{Li}$的数量。

$$A_{ij}^{Li}(A{T}_{Li})=\sum _{A{T}_{Li}\in G_{Li}}\frac{[num(tail)+num(head)]\cdot num(a_{\tau })}{num{\left(a_{ij}^{Li}\right)}^2}(8)$$

为了使GCN能够在向量空间中尽可能紧密地嵌入等价实体，本节使用一组已知的对齐种子AP作为训练数据来训练GCN模型。基于边际排序的优化的关系嵌入损失函数如公式(9)所示。

$$O_{L_i}^S=\sum _{R{T}_{Li}\in AP}\sum _{R{T}_{Li}^{{}^{\prime }}\in A{P}^{{}^{\prime }}}max(0,f_{R_{\tau Li}}(R{T}_{Li})+{\mu }_S-f_{R_{\tau Li}}(R{T}_{Li}^{{}^{\prime }}\left)\right)(9)$$

R T L i = { ( h L i , r τ L i , t L i ) ∈ G L i } ; R T L i ′ = { ( h L i ′ , r τ L i , t L i ) ∣ h L i ′ ∈ E L i } ∪ { ( h L i , r τ L i , t L i ′ ) ∣ t L i ′ ∈ E L i } ( 10 ) \begin{array}{rcl}RT_{Li}&=&\{(h_{Li},r_{\tau Li},t_{Li})\in G_{Li}\};\\RT_{Li}^{'}&=&\{\big(h_{Li}^{'}, r_{\tau Li}, t_{Li}\big)\big|h_{Li}^{'}\in E_{Li}\big\}\cup\big\{\big(h_{Li}, r_{\tau Li}, t_{Li}^{'}\big)\big|t_{Li}^{'}\in E_{Li}\big\}\end{array}\quad(10) RTLi​RTLi′​​==​{(hLi​,rτLi​,tLi​)∈GLi​};{(hLi′​,rτLi​,tLi​) ​hLi′​∈ELi​}∪{(hLi​,rτLi​,tLi′​) ​tLi′​∈ELi​}​(10)

$$f_{R_{\tau Li}}(T_{Li})=\parallel {\mathbf{h}}_{Li}-{\mathbf{t}}_{Li}{\parallel }_1;f_{R_{\tau Li}}(R{T}_{Li}^{{}^{\prime }})=\parallel {\mathbf{h}}_{Li}^{{}^{\prime }}-{\mathbf{h}}_{Li}^{{}^{\prime }}{\parallel }_1(11)$$

其中$f_{R_{\tau Li}}(T_{Li})$表示关系三元组$R_{\tau Li}$中$h_{Li}$和$t_{Li}$之间的$l_1$距离，$R{T}_{Li}^{{}^{\prime }}$表示关系三元组$R{T}_{Li}$的负采样关系三元组，用$G_{Li}$中随机选择的实体替换$h_{Li}$或$t_{Li}$。${\mu }_S>0$是区分正实体对齐和负实体对齐的边缘超参数。

类似地，属性嵌入损失函数如式(12)所示，其中$f_{A_{\tau Li}}(T_{Li})$表示属性三元组$A_{\tau Li}$中$h_{Li}$与$v_{Li}$之间的$l_1$距离，$A{T}_{Li}^{{}^{\prime }}$表示属性三元组$A_{\tau Li}$的负采样属性三元组。${\mu }_A>0$是区分正实体对齐和负实体对齐的边缘超参数。

$$O_{L_i}^A=\sum _{A{T}_{Li}\in AP}\sum _{A{T}_{Li}^{{}^{\prime }}\in A{P}^{{}^{\prime }}}max(0,f_{A_{rLi}}(A{T}_{Li})+{\mu }_A-f_{A_{rLi}}(A{T}_{Li}^{{}^{\prime }}\left)\right)(12)$$

A T L i = { ( h L i , a τ L i , ν L i ) ∈ G L i } ; A T L i ′ = { ( h L i ′ , a τ L i , ν L i ) ∣ h L i ′ ∈ E L i } ∪ { ( h L i , a τ L i , ν L i ′ ) ∣ v L i ′ ∈ A T L i } ( 13 ) \begin{array}{rcl}AT_{Li}&=&\{(h_{Li},a_{\tau Li},\nu_{Li})\in G_{Li}\};\\AT_{Li}^{'}&=&\{\big(h_{Li}^{'},a_{\tau Li},\nu_{Li}\big)|h_{Li}^{'}\in E_{Li}\big\}\cup\big\{\big(h_{Li},a_{\tau Li},\nu_{Li}^{'}\big)|v_{Li}^{'}\in AT_{Li}\big\}\end{array}\quad(13) ATLi​ATLi′​​==​{(hLi​,aτLi​,νLi​)∈GLi​};{(hLi′​,aτLi​,νLi​)∣hLi′​∈ELi​}∪{(hLi​,aτLi​,νLi′​)∣vLi′​∈ATLi​}​(13)

$$f_{A_{\tau Li}}(T_{Li})=\parallel {\mathbf{h}}_{Li}-{\mathbf{v}}_{Li}{\parallel }_1;f_{A_{\tau Li}}(A{T}_{Li}^{{}^{\prime }})=\parallel {\mathbf{h}}_{Li}^{{}^{\prime }}-{\mathbf{v}}_{Li}^{{}^{\prime }}{\parallel }_1(14)$$

为了更清楚地展示关系和属性嵌入学习模块的具体内容，本部分使用示意图进行具体说明，如图4所示。

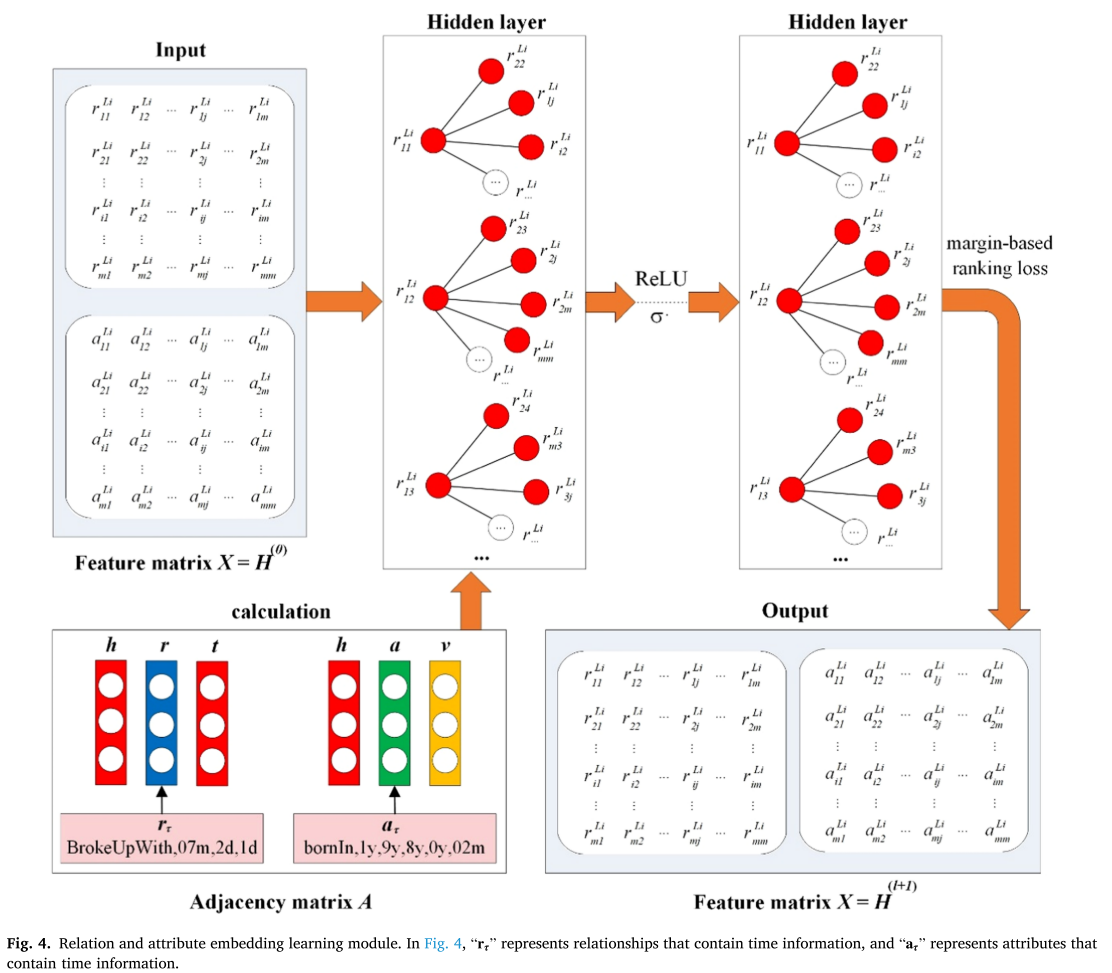
3.3.3. Joint learning of cross-lingual temporal knowledge graphs

3.3.1和3.3.2节中提到的实体、关系和属性嵌入学习模块通常在不同语言的KG中分别学习。为了实现最佳对齐性能，必须对获得的实体嵌入、关系嵌入和属性嵌入进行联合嵌入学习。CTEA的基本思想是通过实体嵌入将不同语言的实体嵌入到一个统一的向量空间中，其中等价实体尽可能接近，然后根据嵌入空间中实体之间的距离找到对齐的实体。我们通过基于对齐的种子执行联合嵌入来实现这一点。

在该模型中，实体嵌入、关系嵌入和属性嵌入的损失函数$O_{L_i}^E$、$O_{L_i}^S$和$O_{L_i}^A$相互独立，分别进行优化。在实验中，随机梯度下降法(SGD)被用来最小化上述损失函数。

在嵌入学习模块中学习了实体嵌入、关系嵌入和属性嵌入。该跨语言时序知识图谱中的实体对齐的目标是优化公式(15)中的联合损失函数$O_{L_i}^K$。

$$O_{L_i}^K=O_{L_i}^E+O_{L_i}^S+O_{L_i}^A(15)$$

其中$O_{L_i}^E$、$O_{L_i}^S$和$O_{L_i}^A$分别表示实体嵌入、关系嵌入和属性嵌入的损失函数。

跨语言时序知识图嵌入模块的整体嵌入过程如下：首先，进入跨语言时序知识图$G_{L1}$和$G_{L2}$，根据实体的属性个数初始化$E_{Li}^{(0)}$，并使用均值为0、标准差为0.01的正态分布初始化权重$M_{Li}^{(0)}$。然后，进行实体嵌入学习。在构造邻接矩阵$A$之后，计算$E_{Li}^{(0)}$的第$l+1$层的输出结果$E_{Li}^{(l+1)}$，并且$E_{Li}^{(l+1)}$的嵌入学习受到 log-max损失函数的限制。其次进行关系和属性嵌入学习，分别构造关系和属性的邻接矩阵$A$，分别计算第$l+1$层关系和属性的输出$E_{Li}^{R_{\tau }Li(l+1)}$和$E_{Li}^{A_{\tau }Li(l+1)}$，然后用损失函数约束$E_{Li}^{R_{\tau }Li(l+1)}$和$E_{Li}^{A_{\tau }Li(l+1)}$的嵌入学习。同时，利用并损函数对实体、关系和属性嵌入的学习进行约束。最后输出嵌入结果$E_{Li}^{(l+1)}$、$E_{Li}^{R_{\tau }Li(l+1)}$和$E_{Li}^{A_{\tau }Li(l+1)}$。

3.4. Alignment of temporal knowledge graphs

实体对齐模块设计了距离计算公式和相似度计算公式，将邻域相似度计算和向量相似度计算相结合，使实体对齐结果更加可信；CTEA从实体的结构信息和属性信息中学习嵌入信息，将实体嵌入、结构嵌入和属性布特嵌入的结果进行融合，得到准确的对齐结果。比如亲戚的出生地比亲戚的生活更重要，因为一个人只能出生在一个地方，却可以生活在多个地方。基于此，如果我们知道两个实体代表同一个人，就可以推断出它们的邻居也代表了关系发源地的同一个地方。根据GCN向量空间中两个不同语言时序知识图的实体/关系/属性值之间的距离来判断最终的对齐结果。首先，通过距离计算公式(16-19)，生成根据从小到大的距离排列的实体对的排序列表。然后将列表中的实体对用作候选对齐实体对以用于相似性计算，以生成最终的实体对齐结果。

实体-实体、关系-关系、属性-属性对之间的距离计算如公式(16)所示。其中$k_m^{L1}$是使用$L_1$语言的实体/关系/属性，$k_n^{L2}$是使用$L_2$语言的实体/关系/属性(其中k是两个KG中的相同类型)。$\parallel k_m^{L1}-k_n^{L2}{\parallel }_1$表示曼哈顿距离，即$l_1$距离。

$$D(k_m^{L1},k_n^{L2})=\parallel k_m^{L1}-k_n^{L2}{\parallel }_1(16)$$

关系-属性和属性-关系对之间的距离计算如公式(17)所示。其中$u_m^{L1}$表示使用$L_1$语言的关系/属性，$w_n^{L2}$表示使用$L_1$语言的属性/关系。$D(u_m^{L1},w_n^{L2})$等价于$\parallel u_m^{L1}-w_n^{L2}{\parallel }_2$，这是欧几里得距离，即$l_2$距离。

$$\mathrm{D}({\mathrm{u}}_{\mathrm{m}}^{\mathrm{L}1},{\mathrm{w}}_{\mathrm{n}}^{\mathrm{L}2})=\left(\sum _{\mathrm{i}=1}^{\mathrm{n}}\right({\mathbf{u}}_{\mathrm{m}}^{\mathrm{L}1}-{\mathbf{w}}_{\mathrm{n}}^{\mathrm{L}2}{)}^2{)}^{\frac{1}{2}}(17)$$

实体-关系对和实体-属性对之间的距离分别如公式(18)和公式(19)所示来计算。其中$e_m^{\mathrm{L}1}$是使用$L_1$语言的任何实体，$u_n^{\mathrm{L}2}$是使用$L_2$语言的任何关系/属性。$h_{Li}(e_m^{L1})$表示$e_m^{L1}$的实体嵌入，$h_{Li}^{R_{\tau }}(u_n^{\mathrm{L}2})$表示$u_n^{\mathrm{L}2}$的关系嵌入，$h_{Li}^{A_{\tau }}(u_n^{\mathrm{L}2})$表示$u_n^{\mathrm{L}2}$的属性嵌入$f(a,b)=\parallel a-b{\parallel }_1$是曼哈顿距离。因为$G_{L1}$和$G_{L2}$的关系和属性的数量不一定相等，即可以存在$|R_{\tau L1}|\ne |R_{\tau L2}|\cup |A_{\tau L1}|\ne |A_{\tau L2}|$，则该模块中$G_{L1}$和$G_{L2}$输出的关系向量和属性向量的维数分别用$d_{R_{\tau }}$和$d_{A_{\tau }}$表示。然后，在公式(17)中，$d_{R_{\tau }}=d_{RL1}+d_{RL2}$表示$G_{L1}$和$G_{L2}$之间的关系嵌入的特征向量的维数。$d_{A_{\tau }}=d_{AL1}+d_{AL2}$表示属性嵌入的特征向量的维数。同样，关系实体与属性实体之间的距离计算也可以用$D(e_m^{L2},u_n^{L1})$和$D(e_m^{L2},w_n^{L1})$来计算。

$$D(e_m^{L1},u_n^{L2})=\delta \frac{f\left(h_{Li}\right(e_m^{L1}),h_{Li}^{R_r}(u_n^{L2}\left)\right)}{d_{R_r}}+(1-{\delta }_1)\frac{f\left(h_{Li}^{R_r}\right(e_m^{L1}),h_{Li}^{R_r}(u_n^{L2}\left)\right)}{d_{A_r}}(18)$$

$$D(e_m^{L1},w_n^{L2})=\delta \frac{f\left(h_{Li}\right(e_m^{L1}),h_{Li}^{A_r}(u_n^{L2}\left)\right)}{d_{R_r}}+(1-{\delta }_2)\frac{f\left(h_{Li}^{A_r}\right(e_m^{L1}),h_{Li}^{A_r}(u_n^{L2}\left)\right)}{d_{A_r}}(19)$$

该模块计算的距离对于等价实体非常小，而对于非等价实体非常大。对于$G_{L1}$中的实体$e_m^{\mathrm{L}1}$，该模块计算$e_m^{\mathrm{L}1}$与$G_{L2}$中的所有实体、关系和属性之间的距离，然后返回排名(从小到大)实体列表 R L = { a p 1 , a p 2 , . . . , a p n } RL=\{ap_{1}, ap_{2},..., ap_{n}\} RL={ap1​,ap2​,...,apn​}，其中$a{p}_i$表示对齐对 $(e_m^{L1},e_n^{L2}),(u_m^{L1},u_n^{L2}),(w_m^{L1},w_n^{L2}),(e_m^{L1},u_n^{L2}),(e_m^{L1},w_n^{L2}),(u_m^{L1},w_n^{L2}),(w_m^{L1},u_n^{L2})$ 作为实体对齐候选集。

通过计算嵌入向量之间的距离，我们可以得到一个按距离从小到大排列的列表$RL$。然后，$RL$被用作候选集来验证实体的相似性，并且其相似性可以通过嵌入结果来计算。对于任意一对单位数$(e_m^{L1},e_n^{L2})$，计算方法如公式(20)所示。

$$Sim(e_m^{L1},e_n^{L2})=cos(e_m^{L1},e_n^{L2})(20)$$

其中$e_m^{L1}\in G_{L1}$且$e_n^{\mathrm{L}2}\in G_{L2}$。给定阈值${\theta }_E=0.6$，如果$Sim(e_m^{L1},e_n^{L2})>{\theta }_E$，则$(e_m^{L1},e_n^{L2})$是对齐实体对。这个阈值${\theta }_E$是通过我们对预对齐实体对的实验获得的结果。当${\theta }_E\ge 0.6$时，可以满足预对齐实体对的预期结果。

为了更清楚地示出在实体对齐模块中提出的方法，使用图5详细示出了所提出的模块的详细过程。

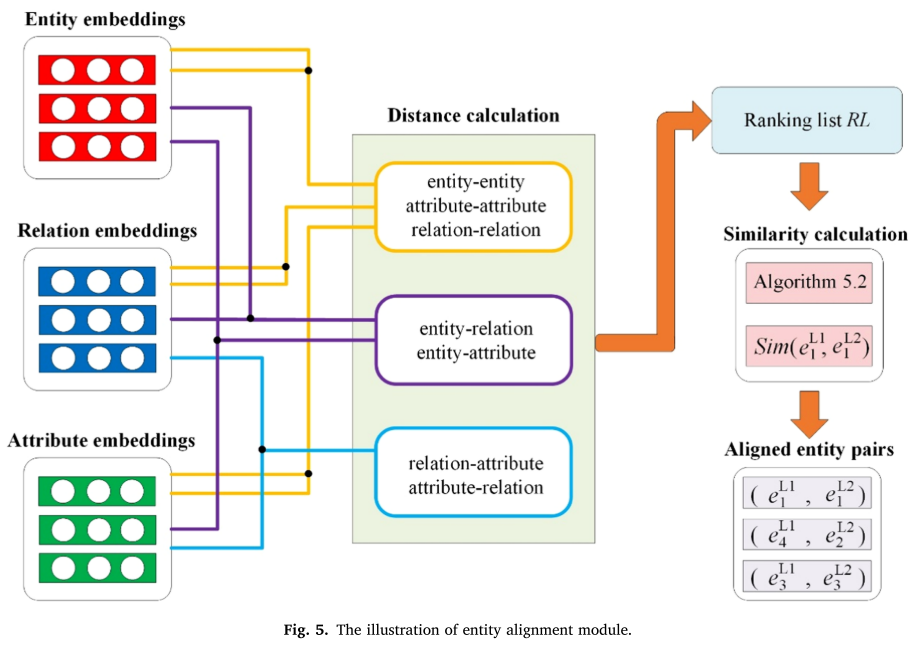
因为列表$RL$不仅包含实体-实体对，而且包含关系-关系对、属性-属性对、实体-关系对、实体-属性对、关系-属性对和属性-关系对。本节提出了一个算法来解决这个问题，如算法1所示。

在算法1中，输入是列表$RL$、关系三元组$R_{\tau Li}$、属性三元组$A_{\tau Li}$和阈值${\theta }_E$。首先计算元素之间的距离(第1行)。在第一种情况下，对于实体-关系对和实体-属性对，右边的关系/属性被分配给其头实体在第二种情况下，对于关系-实体对和属性-实体对，将它们的左侧关系标识符/属性分配给它们的头部实体在第三种情况下，对于关系-属性对和属性-关系对，分别将左和右关系/属性分配给它们的头实体(第8-13行)；对于其他情况：实体-实体对、关系-关系对和属性-属性对，相似性计算与上述结果一起沿着(第14-15行)。当$im>{\theta }_E$时，实体对被添加到对齐的实体对集合$AE$。最后，该算法成功地输出了对齐的实体对$AE$。

4. Experiments

4.1. Datasets and settings

环境。 我们在工作站上进行了实验，工作站采用Intel®Core™i9-9900 2.80GHz CPU、32 GB内存和GeForce GTX 2080 Ti。

数据集。 CTEA分别在稀疏数据集和密集数据集的15 K数据集上进行了测试，以确保结果的无偏倚评价。稀疏关系数据集和密集关系数据集是由IDS算法生成的报告。本节选择了三个众所周知的包含时态信息的知识图作为数据源：DBpedia(英语)、DBpedia(法语)和DBpedia(德语)。在此基础上，生成了15 K规模实体的DBpedia(英法)数据集和DBpedia(英德)数据集。然后我们使用了两个稀疏数据集：DBpedia(英语和法语)(15 K)和DBpedia(英语和德语)(15 K)；以及两个密集数据集：DBpedia(英语和法语)(15 K)和DBpedia(英语和德语)(15 K)。在知识库(KB)中，每条信息都以三重格式(实体、属性、值)表示，其中值可以是文字或其他实体。$RT$代表具有时间特性的关系，而$AT$代表具有时间特性的属性。(对于时间，我们在数据集中统一处理成如下格式，例如：1987-12-31：1 y，9 y，8 y，7 y，12 m，31 d)。对于每个数据集，事实被分成三个子集：训练集(20%)、验证集(10%)和测试集(70%)。数据集的统计数据如表3所示，其中$T\tau$是包含时间信息的三元组。

评估指标。 在我们的实验中，默认的对齐方向是从左到右。以DBpedia(英语&德语)为例。我们将 DBpedia(英语)作为源，并将其与目标知识图谱 DBpedia(德语)对齐。遵循约定，我们使用 Hits@m (1, 5, 10)(即在前 m 个预测中排名正确对齐的实体的比例)、平均排名 (MR)(即匹配实体的平均值)和平均倒数排名(MRR)作为评价指标。当然，较高的 Hits@m 和 MRR 分数以及较低的 MR 分数表明性能较好。

参数设置。 实验中，采用贪婪搜索来寻找模型的最佳超参数，并采用随机梯度下降(SGD)作为优化器。 GCN的层数设置为2。$O_{L_i}^E$的正偏差$\beta$设置为2。损失函数中${\mu }_S,{\mu }_A$设置为3，${\delta }_1$和${\delta }_2$的值设置为0.9。嵌入维度 $d_{R_{\tau }}$ 和 $d_{A_{\tau }}$ 的值分别设置为 1000 和 100。 实验中，$O_{L_i}^E$、$O_{L_i}^S$和$O_{L_i}^A$模型在DBpedia(English&French)(15K)和DBpedia(English&Derman)(15K)数据集上的训练数据批次为5000个，最大训练次数为2000个epoch。

4.2. Baselines

对于跨语言时序知识图谱实体对齐的任务，选择CTEA、JAPE、SEA、AliNet和KEGCN、Tem-EA作为基线进行比较。

JAPE 提出了一种基于嵌入的跨语言实体对齐方法，该方法不依赖于跨语言知识图谱之间的机器翻译。通过结合两个知识图谱的关系三元组和结构嵌入，首先提出在保留跨语言知识图谱属性信息的同时学习跨语言实体嵌入，并利用知识图的属性三元组和属性嵌入进一步细化嵌入。

SEA 提出了一种半监督的方法来解决实体对齐问题，该方法不仅使用给定的对齐实体，而且还考虑未对齐的实体以提高性能。指出了实体度差对知识图嵌入的影响，并在对抗训练框架下提高了知识图嵌入中度差的意识，从而解决了这一问题。

AliNet 提出了一种新的知识图对齐算法网络，其目的是以端到端的方式缓解邻域结构的非同构性。由于模式的异质性以及对应实体的直接邻居通常不同，AliNet引入远邻居来扩大邻居结构之间的重叠。它使用一个注意力机制，以突出有用的远邻居和减少噪音，然后使用门控机制来控制直接和远邻居信息的聚合。此外，它还提出了一个关系损失细化实体表示。

KE-GCN 提出了一种新的框架–基于知识嵌入的图卷积网络(KE-GCN)，它结合了GCN在基于图的信念传播中的能力和先进的知识库嵌入方法的优点，并摒弃了它们的局限性。理论分析表明，KE-GCN是几种著名的GCN方法的统一，具有图卷积的新视角。

Tem-EA 提出了一种创新的实体对齐方法，Tem-EA，专为时序知识图谱(TKG)。Tem-EA使用LSTM(长短期记忆)来获取时间序列表示，然后将它们与结构信息表示集成，以创建全面的实体嵌入结果。此外，Tem-EA引入了最近邻匹配的概念，以提高实体对齐的精度。

4.3. Experiment Results

4.3.1. Results of CTEA on different datasets

在DBpedia(英语和法语)数据集和DBpedia(英语和德语)数据集上执行CTEA的结果如表4所示。从表中可以看出，与同类数据集相比，CTEA在密集数据集上的性能优于稀疏数据集。这是因为密集数据集中的事实包含更多的关系三元组。CTEA采用GCN和翻译模型TransE，从实体的邻域和关系角度获取嵌入信息，使CTEA能够捕捉到更多的语义信息。CTEA在DBpedia(英语和德语)数据集上的表现更好，在不同的数据集上具有相同的稀疏度。从表3中可以看出，DBpedia(英语和德语)数据集中的属性三元组的数量高于DBpedia(英语和法语)数据集，这导致了两个数据集上CTEA结果的差异。可以得出结论，所提出的跨语言时序知识图实体对齐模型CTEA，当处理相同类型的数据集时，在密集数据集比稀疏数据集取得更好的结果。

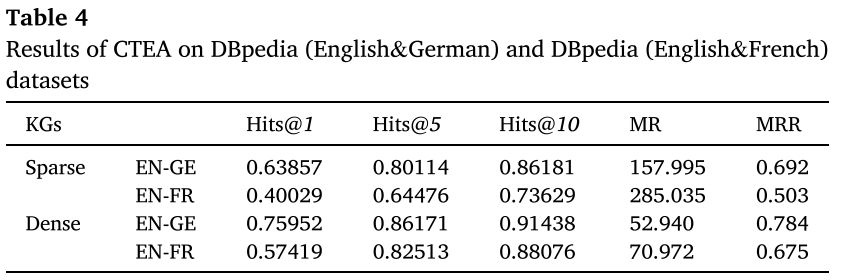
4.3.2. Results of different methods on DBpedia(English&German) datasets

本节比较了六种方法，包括：JAPE，SEA，AliNet，KE-GCN和Tem-EA。在表5中，比较了6种方法在DBpedia(英语和德语)数据集上进行的Hits@1、Hits@5、Hits@10、MR和MRR的结果。

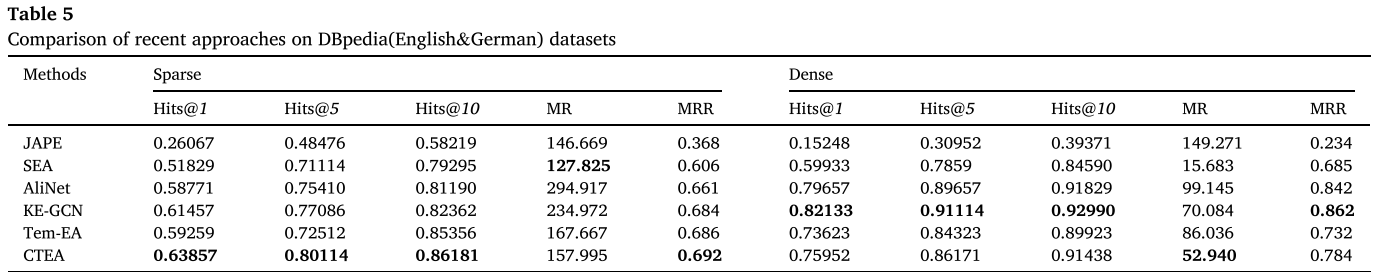
通过对稀疏数据集的观察可以发现，在稀疏DBpedia(English&German)数据集的执行结果中，CTEA的Hits@m值和MRR值均优于其他模型，SEA模型的MR值最好。但在密集数据集上，可以发现在密集DBpedia(English &German)数据集上的执行结果并不理想。KE-GCN模型的性能最好，其Hits@k值和MRR值均高于其他模型，而CTEA模型的MR值性能最好。通过对KE-GCN模型的分析，发现它还将先进的知识嵌入模型与GCN相结合，这是其性能优异的重要原因。与KE-GCN算法相比，CTEA算法更适合处理稀疏数据集。

4.3.3. Results of different methods on DBpedia(English&French) datasets

在表6中，比较了在DBpedia(英语和法语)数据集上通过六种方法执行的Hits@1、Hits@5、Hits@10、MR和MRR的结果。通过表6的观察可以看出，CTEA的Hits@m值和MRR值均优于其他模型，JAPE和SEA的MR值分别最好。根据表4，DBpedia(英语和法语)中的三元组数量少于DBpedia(英语和德语)，这表明CTEA在处理稀疏关系时更有利，因为在所提出的CTEA模型中应用了transE。

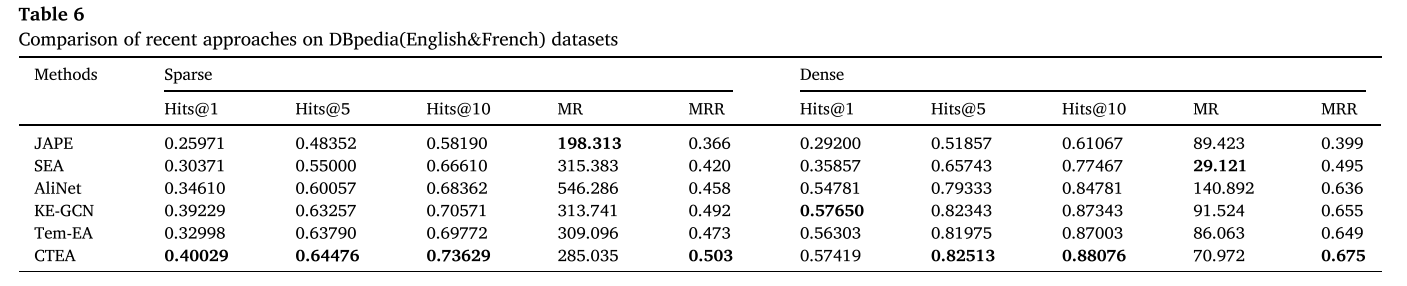
结合所有模型之间的比较，尽管所有模型在密集数据集上具有更高的Hits@m值和MRR值，但CTEA模型在稀疏数据集上的表现优于使用GCN方法的模型。实验结果表明，CTEA模型由于引入了翻译模型TransE，在处理稀疏关系方面具有更大的优势，在稀疏数据集上的性能优于其他模型。

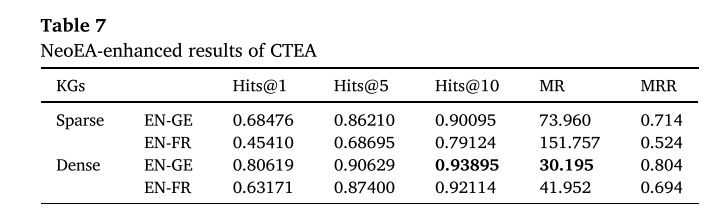
4.3.4. Entity alignment performance enhancing by NeoEA

NeoEA 是2022年提出的一种用于实体对齐的原则表示学习方法。该模型不仅基于几何距离增加了对齐实体的接近度，而且通过消除嵌入分布与底层本体知识之间的差异，实现了两个知识图谱的神经本体对齐。

现将其应用于所提出的模型CTEA，具体结果见表7。与表4相比，可以看出，通过应用NeoEA(一种主表征学习方法)，CTEA(一种跨语言时序知识图实体对齐方法)在所有指标上都有所改善。其中，Hits@m结果增加了5个百分点。除在密集DBpedia(English&德国)数据集上的结果外，其他指标均高于KE-GCN。

4.3.5. Ablation Study

为了进一步评估模型的有效性，我们构建了两个基于CTEA的消融实验，即CTEA(w/o Attribute)和CTEA(w/o Timing)。CTEA(w/o Attribute)是指删除CTEA中嵌入的属性模块。CTEA(w/o Timing)是指在删除时间信息的数据集上进行的实验。结果见表8和表9。与CTEA相比，CTEA(w/o Attribute)和CTEA(w/o Timing)在相应数据集上的性能都有所下降。具体来说，我们观察到CTEA(w/o Attribute)有最大的性能下降，其次是CTEA(w/oTiming)，这证实了属性信息和时间信息是非常重要的跨语言实体对齐的效果。

4.4. Defects analysis

在Hits@m、MR和MRR方面与其他方法相比，CTEA在跨语言时序知识图的实体对齐方面有很大的改进。与次优模型相比，在DBpedia(英语和德语)数据集上执行的Hits@m值增加了两个百分点，在DBpedia(英语和法语)数据集上执行的Hits@m值增加了一个百分点。在NeoEA对实体对齐效果进行改进后，CTEA的结果在Hits@m值方面比原来的结果提高了5个百分点以上，但仍然存在一定的局限性：

1. 表4显示CTEA在具有大量关系三元组和属性三元组的数据集中表现更好，也就是说，它在15K密集数据集中表现得更好。因此，CTEA缺乏对稀疏数据集的处理，而现实中的时序知识图通常是稀疏的。对于稀疏关系，我们可以使用更先进的翻译模型或图神经网络来改进它们。
2. CTEA解决了跨语言时序知识图的实体对齐问题，但实体对齐只是知识图融合的核心内容。为了解决时序知识图之间的知识共享问题，时序知识图的融合还需要进一步研究。

5. Conclusion and future work

近年来，随着大数据时代的到来，时序知识图谱发展迅速，其数据规模不断增大。如何提高非同源时序知识图的利用率，并将其中重复出现的事实进行物理对齐是本文的研究重点。鉴于GCN擅长从实体角度学习嵌入，而翻译模型擅长从关系角度学习嵌入，提出了一种基于GCN和TransE的跨语言时序知识图实体对齐方法。CTEA从实体、关系和属性的角度设计了一种基于GCN和TransE的联合嵌入方法，增强了时序知识图的嵌入学习效果。此外，CTEA将邻域的距离计算和实体嵌入的相似度计算结合在实体对齐模块中，使实体对齐结果更加可靠。最后，在真实的数据集上进行的大量实验结果表明，CTEA在跨语言时序知识图谱的实体对齐度量上优于现有模型。

对于时序知识图谱的实体对齐，本文取得了一定的进展，具体原因将在以后分析并考虑改进，以提高跨语言时序知识图的实体对齐效果。最后，未来会考虑结合真实的场景中的超大规模时序知识图谱对模型进行优化。

论文原文：https://www.sciencedirect.com/science/article/abs/pii/S0893608024000595

GitHub：https://github.com/DMKE-Lab/CTEA