剑指offer 30. 包含min函数的栈

news2025/1/16 5:35:58

原题链接

题目描述

解决方案

思路分析

核心思路

流程图解

操作细节

代码实现

Python 语言实现

C 语言实现

Java 语言实现

复杂度分析

总结

其他相似题目

原题链接

剑指offer_在线编程_牛客网 (nowcoder.com)

题目描述

定义一个栈的数据结构，并实现一个能够在常数时间内（O(1)）获取栈的最小元素的min函数。要求在该栈中，调用min、push以及pop的时间复杂度都是O(1)。

题目要求各函数的调用总次数不超过20000次。

解决方案

思路分析

要在O(1)时间复杂度内实现获取栈的最小值，我们需要借助辅助栈来存储当前栈中每个元素入栈时的最小值。辅助栈中的栈顶元素始终是当前主栈中的最小元素。

核心思路

主栈（stack）：用于存储所有入栈的元素。
辅助栈（minStack）：用于存储主栈中对应位置的最小值。

流程图解

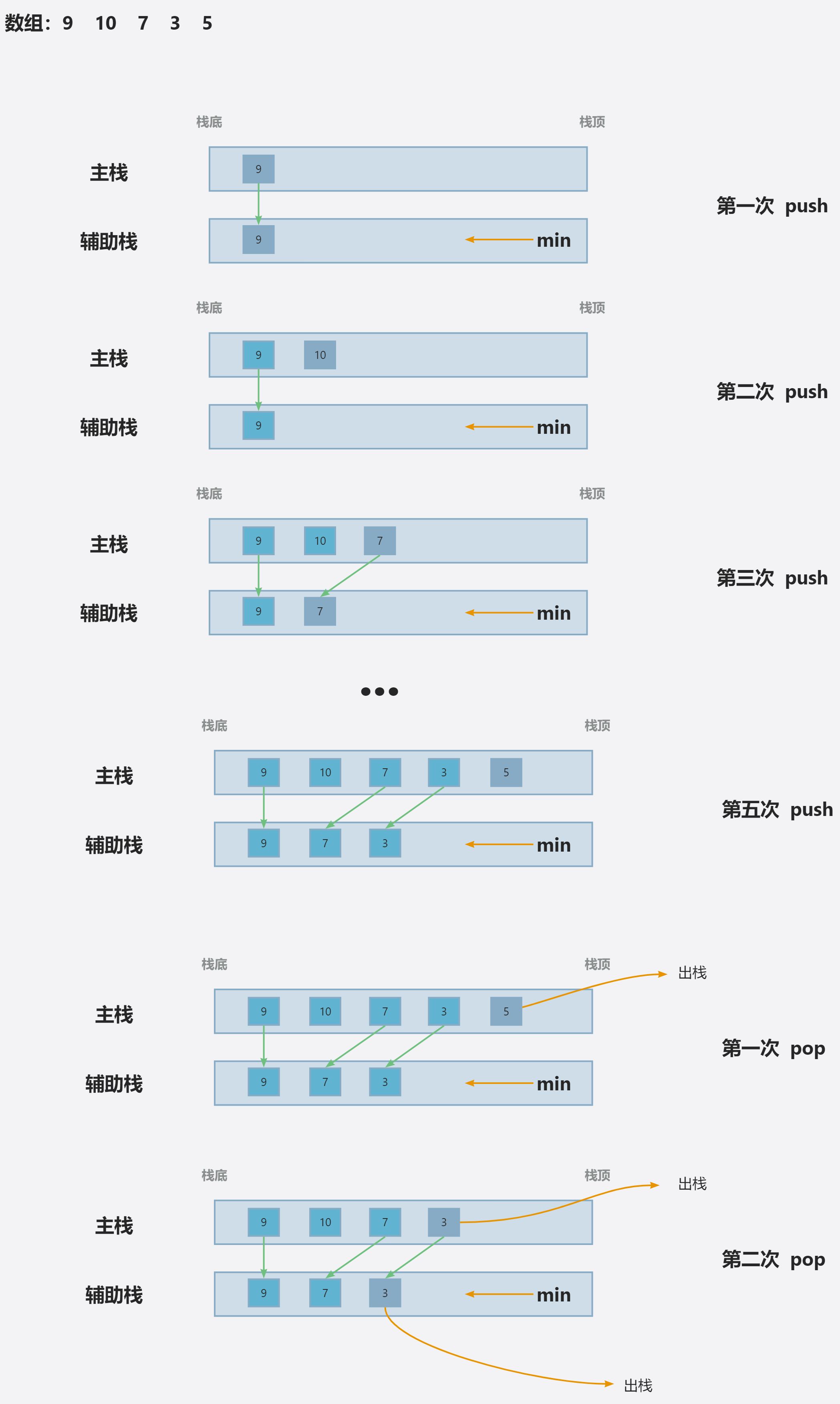
操作细节

push操作：将元素压入主栈，同时将该元素与当前辅助栈的栈顶元素（即当前最小值）进行比较。如果该元素小于或等于当前最小值，则也将该元素压入辅助栈。
pop操作：弹出主栈栈顶元素。如果该元素等于辅助栈的栈顶元素，则同时弹出辅助栈的栈顶元素。
min操作：直接返回辅助栈的栈顶元素，即当前栈中的最小值。

代码实现

下面是不同语言的代码实现：

Python 语言实现

class MinStack:
    def __init__(self):
        self.stack = []  # 主栈
        self.minStack = []  # 辅助栈，存储最小值

    def push(self, val: int) -> None:
        self.stack.append(val)
        if not self.minStack or val <= self.minStack[-1]:
            self.minStack.append(val)

    def pop(self) -> None:
        if self.stack:
            if self.stack[-1] == self.minStack[-1]:
                self.minStack.pop()
            self.stack.pop()

    def top(self) -> int:
        if self.stack:
            return self.stack[-1]
        return -1  # 栈为空时返回-1

    def min(self) -> int:
        if self.minStack:
            return self.minStack[-1]
        return -1  # 栈为空时返回-1

C 语言实现

#include <stdio.h>
#include <stdlib.h>
#include <limits.h>

typedef struct StackNode {
    int data;
    struct StackNode* next;
} StackNode;

typedef struct {
    StackNode* top;
    StackNode* minTop;
} MinStack;

MinStack* minStackCreate() {
    MinStack* stack = (MinStack*)malloc(sizeof(MinStack));
    stack->top = NULL;
    stack->minTop = NULL;
    return stack;
}

void push(MinStack* stack, int val) {
    StackNode* node = (StackNode*)malloc(sizeof(StackNode));
    node->data = val;
    node->next = stack->top;
    stack->top = node;

    if (stack->minTop == NULL || val <= stack->minTop->data) {
        StackNode* minNode = (StackNode*)malloc(sizeof(StackNode));
        minNode->data = val;
        minNode->next = stack->minTop;
        stack->minTop = minNode;
    }
}

void pop(MinStack* stack) {
    if (stack->top == NULL) return;
    if (stack->top->data == stack->minTop->data) {
        StackNode* minNode = stack->minTop;
        stack->minTop = stack->minTop->next;
        free(minNode);
    }
    StackNode* temp = stack->top;
    stack->top = stack->top->next;
    free(temp);
}

int top(MinStack* stack) {
    return stack->top ? stack->top->data : -1;
}

int min(MinStack* stack) {
    return stack->minTop ? stack->minTop->data : -1;
}

void minStackFree(MinStack* stack) {
    while (stack->top != NULL) {
        StackNode* temp = stack->top;
        stack->top = stack->top->next;
        free(temp);
    }
    while (stack->minTop != NULL) {
        StackNode* temp = stack->minTop;
        stack->minTop = stack->minTop->next;
        free(temp);
    }
    free(stack);
}

Java 语言实现

import java.util.Stack;

class MinStack {
    private Stack<Integer> stack;
    private Stack<Integer> minStack;

    public MinStack() {
        stack = new Stack<>();
        minStack = new Stack<>();
    }

    public void push(int val) {
        stack.push(val);
        if (minStack.isEmpty() || val <= minStack.peek()) {
            minStack.push(val);
        }
    }

    public void pop() {
        if (!stack.isEmpty()) {
            if (stack.peek().equals(minStack.peek())) {
                minStack.pop();
            }
            stack.pop();
        }
    }

    public int top() {
        return stack.isEmpty() ? -1 : stack.peek();
    }

    public int min() {
        return minStack.isEmpty() ? -1 : minStack.peek();
    }
}