「数组」数组双指针算法合集：二路合并|逆向合并|快慢去重|对撞指针 / LeetCode 88|26|11（C++）

news2025/1/13 15:31:46

概述

1.二路合并

思路

复杂度

Code

2.逆向合并

思路

复杂度

Code

3.快慢去重

思路

复杂度

Code

4.对撞指针

思路

复杂度

Code

总结

概述

数组的线性枚举是我们学习编程时遇到的第一种枚举手段。但是它看起来有点愚蠢：只有一个索引i承担全部的工作，如果有第二个索引j，它总是被嵌套在一次for循环的内部。

像这样：

for (int i = 0;i < n;i++){
   for(int j = i;j < n;j++)
      ...
}

这种行为看起来很直观，但是使得这段代码的复杂度达到了O(n²) 。

但如果我们这样做呢?

for (int i = 0,j = 0;i < n;i++){
   ...
}

在一次循环内维护两个下标索引的行为叫做双指针，如你所见，这一层for循环的时间复杂度是线性的。

来看看它具体是怎么用的。

1.二路合并

思路

二路合并就是将两个有序数组合成一个有序数组。

我们希望将两个指针指向了两个有序数组，只遍历一次就能够完成合并操作。尽管很简单，但这是归并排序的核心操作之一。

事实上，我们需要三个指针：i，j，k。各自指向两个待合并数组nums1、nums2和承载结果的数组ans。

如果nums1[i]<nums2[j]令承载结果的数组ans[k]获得nums1[i]元素，然后i和k后移一位。

否则ans[k]获得nums2[j]元素，然后j和k后移一位。

你会注意到：每轮循环后i和j分别指向两个数组中的待比较的元素，k指向ans数组的待写入位置。

当i或j到达末尾时，将另一方的剩余元素写入ans中。

复杂度

时间复杂度：O(m+n)

空间复杂度：O(m+n)

m、n：两个数组各自长度

Code

vector<int> merge(vector<int>&a,vector<int>&b){
	const int n=a.size(),m=b.size();
	vector<int>ans(n+m);
	int i=0,j=0,k=0;
	while(i<n&&j<m){
		if(a[i]<b[j])ans[k++]=a[i++];
		else ans[k++]=b[j++];
	}
	while(i<n)ans[k++]=a[i++];
	while(j<m)ans[k++]=b[j++];
	return ans;
}

2.逆向合并

在二路合并中，如果没有承接数组ans怎么办？

给定两个排序后的数组 A 和 B，其中 A 的末端有足够的缓冲空间容纳 B。编写一个方法，将 B 合并入 A 并排序。

初始化 A 和 B 的元素数量分别为 m 和 n。

示例：

输入：nums1 = [1,2,3,0,0,0], m = 3, nums2 = [2,5,6], n = 3
输出：[1,2,2,3,5,6]
解释：需要合并 [1,2,3] 和 [2,5,6] 。
合并结果是 [1,2,2,3,5,6] ，其中斜体加粗标注的为 nums1 中的元素。

思路

但是我们有一个容量很大的A。

考虑这样一个问题：A的后面总是能容纳B，所以我们可以对整个合并操作进行逆向调整，也就是从A末尾的空白区域开始写入元素。

如果你写入了A的元素，那么这意味着前面有一个A元素已经失效了，它被转移到了A末尾，在A的前面删掉一个元素，再在末尾加回来，那么A的空余区不变，仍能容纳B。

如果你写入了B的元素，那么占用一格A的空余区。但是A的空余区只在B完全写入时才被填满。

复杂度

时间复杂度：O(m+n)

空间复杂度：O(1)

Code

void merge(vector<int>& nums1, int m, vector<int>& nums2, int n) {
    int i=m-1,j=n-1,k=n+m-1;
    while(i>=0&&j>=0){
        if(nums1[i]<nums2[j])nums1[k--]=nums2[j--];
        else nums1[k--]=nums1[i--];
    }
    while(i>=0)nums1[k--]=nums1[i--];
    while(j>=0)nums1[k--]=nums2[j--];
}

3.快慢去重

给你一个 非严格递增排列 的数组 nums ，请你原地删除重复出现的元素，使每个元素 只出现一次 ，返回删除后数组的新长度。元素的 相对顺序 应该保持一致。然后返回 nums 中唯一元素的个数。

考虑 nums 的唯一元素的数量为 k ，你需要做以下事情：

更改数组 nums ，使 nums 的前 k 个元素包含唯一元素，并按照它们最初在 nums 中出现的顺序排列。nums 的其余元素与 nums 的大小不重要。
返回 k 。

思路

C++标准库在algorithm库下定义了unique函数，实现了这个功能。我们来想一想该怎么实现它。

这种算法必须基于已排序数组实现。

定义快指针fast向后探索，慢指针slow维护去重区。

事实上，我们只依靠fast指针来遍历数组，slow做的工作并不是遍历而是维护fast指针探索的结果。

slow总是指向去重区后的第一个待写入位置，slow-1则为去重区的最后一个位置。

每次都依靠fast指针与slow-1进行比对，然后将可行元素写入slow位置处，随后slow++。

注意要从下标1开始。

复杂度

时间复杂度：O(n)

空间复杂度：O(1)

Code

int removeDuplicates(vector<int>& nums) {
    const int n=nums.size();
    int slow=1,fast=1;
    for(;fast<n;fast++)
       if(nums[fast]!=nums[slow-1])
         nums[slow++]=nums[fast];
    return slow;
}

4.对撞指针

给定一个长度为 n 的整数数组 height 。有 n 条垂线，第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。

找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。

返回容器可以储存的最大水量。

说明：你不能倾斜容器。

示例：

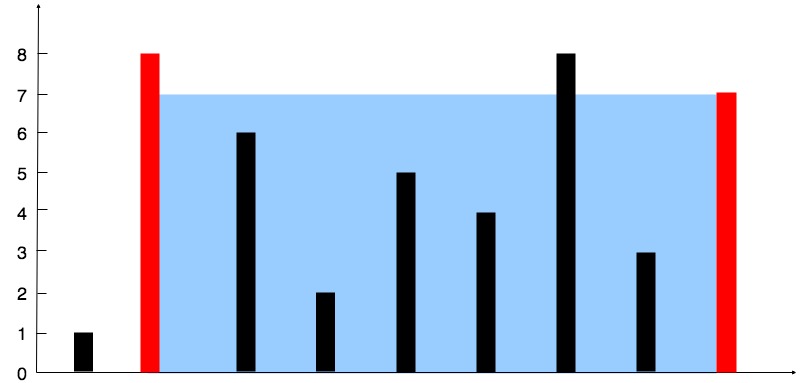
输入：[1,8,6,2,5,4,8,3,7]
输出：49 
解释：图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49。

思路

对撞指针从两个方向同时遍历数组。

定义i=0，j=n-1；分别从两侧向内收缩。

双向遍历往往只收缩i和j的其中一个指针，这意味着我们需要知道i右移和j左移的条件。

我们认识到这样一个问题：遍历时容器底的长度总是减小的。因此，如果希望收缩双指针时容量还能增大，那么必须是指针元素小的一方收缩：容器容量总是由他的短边决定。

复杂度

时间复杂度：O(n)

空间复杂度：O(1)

Code

int maxArea(vector<int>& height) {
    int len=height.size();
    int ans=(len-1)*min(height[0],height[len-1]);
    for(int i=0,j=len-1;i<j;){
       int V=(j-i)*min(height[j],height[i]);
       if(V>ans)ans=V;
       if(height[j]>height[i])i++;
       else j--;
    }
    return ans;
}