欢迎来到博主的专栏:数据结构
博主ID:代码小豪
文章目录
- 二叉搜索树
- 二叉搜索树的声明与定义
- 二叉搜索树的查找
- 二叉搜索树的插入
- 二叉搜索树的中序遍历
- 二叉搜索树的删除
- key_value型搜索二叉树
二叉搜索树
二叉搜索树也称二叉排序树,是具备以下特征的二叉树
(1)每个节点最多拥有两个子节点
(2)对于每个节点,其左子树值均小于根节点,其右子树均大于根节点。
如图:

该二叉树为二叉搜索树,原因如下:
以节点8为根节点,其左子树均小于8,右子树均大于8.

以节点3为根节点,其左子树均小于3,其右子树均大于3.

以此类推。

该二叉树则不为二叉搜索树,因为以节点7为根节点,节点4小于7,却存在于根节点的右子树,因而不符合右子树均小于根节点这一特征。所以不构成搜索二叉树。
搜索二叉树有个重要的规则就是,在二叉树内不能存在两个相同值的节点,因为这会对二叉搜索树的删除结点造成影响。
二叉搜索树的声明与定义
二叉搜索树可以分为两部分,一部分是节点,另一部分则是树
对于节点,其需要记录一个值,以及分别指向左子节点与右子节点的两个指针。
再设计一个构造函数,通过传递key的值来生成该节点,并将左右指针置为空(方法不唯一,只是博主采用这种构造方式)
template<class k>
struct TreeNode
{
TreeNode(const k& key)
:_key(key)
,_left(nullptr)
,_right(nullptr)
{}
k _key;
TreeNode* _left;
TreeNode* _right;
};
接着是设计一个类来控制整个二叉搜索树,只需要定义一个指向二叉树的根节点的指针成员即可。此外,在设计一些搜索二叉树的成员函数,比如查找节点,排序节点,插入节点和删除结点。
template<class k>
class BSTree
{
public:
typedef TreeNode<k> Node;//将节点类型重命名
void find(const k& key);//查找
void insert(const k& key);//插入节点
void erase(const k& key);//删除结点
void inorder();//中序遍历
private:
Node* _root=nullptr;//根节点
};
二叉搜索树的查找
如何在二叉搜索树当中找到值为key的节点呢?当然,直接使用遍历的形式是可行的,但是利用二叉搜索树的特性可以更加高效。
用key值与根节点进行比较,会出现以下三种情况
(1)key比根节点大
(2)key比根节点小
(3)key等于根节点
如果是情况3,那就说明找到key值了,返回查找的结果
若是情况(1),根据二叉搜索树的特征,比根节点大的值都在右子树,因此进入右子树查找
若是情况(2),比根节点小的值都在左子树,因此进入左子树查找。
如果key来到了空节点处,就说明该二叉搜索树没有匹配的节点,因此查找的结果是无。
bool find(const k& key)//查找
{
Node* cur = _root;
while (cur != nullptr)
{
if (key > cur->_key)//比key小,进入右树
cur = cur->_right;
if (key < cur->_key)//比key大,进入左树
cur = cur->_left;
else//与可以相等,返回结果
return true;
}
return false;
}
动画演示1:假设key为7

演示动画2:假设key为9

其实二叉搜索树的查找方式和二分查找的原理非常类似,都是将查找数据的区间一步步缩短,最后确定元素。
二叉搜索树的插入
在二叉搜索树种插入新节点需要解决一个问题
(1)在插入新节点后,如何保持二叉搜索树的性质?
其实也就是搞清楚新节点插入的位置在哪,其实这个问题的解决思路可以参考前面查找节点的方法。
前面提到,通过缩短数据区间,可以在搜索二叉树中定位到元素的位置,我们可以假设待插入的节点已经存在于二叉树当中。通过查找该节点的方式,定位到元素的位置,然后将该节点插入到对应的位置即可。
思路如下:
(1)通过查找的方式缩短区间(即用key对比根节点)
(2)如果走到了空节点,就说明定位到了元素的位置,直接插入即可
(3)如果存在与插入节点相同值的节点,根据二叉搜索树不能存在两个相同节点的特性,停止不合法的插入操作
还存在一种特殊情况,即当二叉搜索树为空树时,此时无法通过查找的方式进行搜索(因为要让key和根节点的值进行比较,但是空树没有根节点),解决方法是直接生成根节点即可。
bool insert(const k& key)//插入节点
{
if (_root == nullptr)
{
_root = new Node(key);
return true;
}
Node* cur = _root;
Node* parent = nullptr;
while (cur != nullptr)
{
if (key > cur->_key)//比key小,进入右树
{
parent = cur;
cur = cur->_right;
}
else if (key < cur->_key)//比key大,进入左树
{
parent = cur;
cur = cur->_left;
}
else//与key相等,不合法的插入操作
return false;
}
//来到空节点处,将新节点插入至该处
cur = new Node(key);
if (key > parent->_key)
parent->_right = cur;
else
parent->_left = cur;
return true;
}
动画演示:

二叉搜索树的中序遍历
中序遍历二叉搜索树,会得到一个升序的结果,先来写出代码,再分析原理。
void inorder()//中序遍历
{
_inorder(_root);
}
void _inorder(Node* root)
{
if (root == nullptr)
return;
_inorder(root->_left);
cout << root->_key<<' ';
_inorder(root->_right);
}
执行如下操作:
int arr[] = { 8, 3, 1, 10, 6, 4, 7, 14, 13 };
BSTree<int> b;
for (auto e : arr)
{
b.insert(e);
}
上述代码的作用是构造出下图的二叉搜索树

再中序遍历该二叉搜索树
b.inorder();
运行结果为:

那么为什么中序遍历会呈现出升序的特征呢?
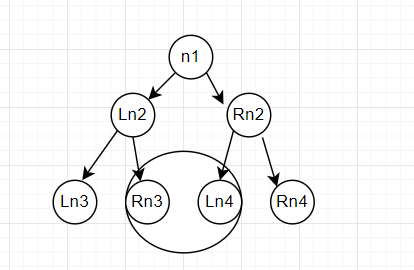
根据二叉搜索树的定义,对于每个根节点来说,其左子树小于根节点,其右子树大于根节点。那么下面这个二叉树的排序为

Ln2<n1<Rn2

Ln3<Ln2<Rn3<n1<Ln4<Rn2<Rn4.
把小于号去掉,即为
Ln3 Ln2 Rn3 n1 Ln4 Rn2 Rn4.
这个顺序既符合中序遍历的顺序,也符合升序的顺序。我们也可以由此得出一个结论
离根节点越左的节点,越小,离根节点越右的节点,越大,越靠近根节点的节点,越接近根节点。比如上图中的Ln4和Rn3.

这个结论将会在二叉搜索树的删除中起到非常大的左右。
二叉搜索树的删除
首先查找元素是否在二叉搜索树中,如果不存在,则返回, 否则要删除的结点可能分下面四种情况:
a. 要删除的结点无子结点

解决方法:直接删除即可。
b. 要删除的结点只有左子结点

删除该结点且使被删除节点的父结点指向被删除节点的左子结点

c. 要删除的结点只有右子结点

删除该结点且使被删除节点的父结点指向被删除结点的右子结点

看起来有待删除节点有4中情况,实际情况a可以与情况b或者c合并起来。
d. 要删除的结点有左、右孩子结点

这种情况下是最麻烦的,因为我们不能贸然的将节点3删除,这会断开二叉搜索树与节点3的左右子树的链接,破坏结构。
换句话说,要删除节点3,就要找到一个节点来替换节点3,这样才能保持住二叉搜索树的特性。那么什么节点可以胜任呢?
为了维持二叉搜索树的特性,因此替换节点的节点应该有以下特征:(1)比左子节点大(2)比右子节点小。因此选取来替换的节点应该越接近待删除的节点越好。
在上一节中提到,越接近根节点的节点,其值也越接近根节点。对于待删除的节点来说,最接近它的值无非两个
(1)其左子树最右边的节点
(2)其右子树最左边的节点
这两个节点都是离待删除节点最近的节点。也是值最接近的节点。因此,选取这两个节点来替换待删除的节点再合适不过了。
删除操作的实现如下:
bool erase(const k& key)//删除结点
{
Node* cur = _root;
Node* parent = cur;
while (cur != nullptr)
{
if (key > cur->_key)//比key小,进入右树
{
parent = cur;
cur = cur->_right;
}
if (key < cur->_key)//比key大,进入左树
{
parent = cur;
cur = cur->_left;
}
else//与key相等,删除该节点
{
if (cur->_left == nullptr)//情况a、b
if (parent->_left = cur)
parent->_left = cur->_right;
else
parent->_right = cur->_right;
else if(cur->_right==nullptr)//情况c
if (parent->_left = cur)
parent->_left = cur->_left;
else
parent->_right = cur->_left;
else//情况d
{
Node* RightMinp = cur;//右子树的最左节点的父节点
Node* RightMin = cur->_right;//右子树的最左节点
while (RightMin->_left != nullptr)
{
RightMinp = RightMin;
RightMin = RightMin->_left;
}
cur->_key = RightMin->_key;//交换节点
if (RightMinp->_right == RightMin)
RightMinp->_right = RightMin->_right;
else
RightMinp->_left = RightMin->_right;
delete RightMin;
}
return true;
}
}
return false;
}
key_value型搜索二叉树
key_value型搜索二叉树与key型搜索二叉树的不同在于,key型二叉树按照key值将节点进行分流,而key_value型搜索二叉树也是按照key值将节点进行分流,但是每个节点还会有一个对应的value值。
以现实距离,每个人可能会有相同的姓名,但是身份证号一定不同,即身份证是每个人的key,key值不能相同,而value值可以相同,通过在key_value型搜索二叉树查找key值非常快的特性,这样存储数据会变得更加灵活。
key_value型搜索二叉树的插入、删除都相同,不同的点在于key_value型搜索二叉树的节点多了一个value值,因此博主不再赘述对应操作,直接给出源代码。
template<class key,class value>
struct kvtreeNode
{
kvtreeNode(const pair<key, value>& kv)
:_kv(kv)
,_left(nullptr)
,_right(nullptr)
{;}
pair<key, value> _kv;
kvtreeNode<key, value>* _left;
kvtreeNode<key, value>* _right;
};
template<class key,class value>
class kvtree
{
public:
kvtree()
:_root(nullptr)
{;}
kvtree(const initializer_list<pair<key, value>>& list)
{
for (const auto& e : list)
{
insert(e);
}
}
typedef kvtreeNode<key, value> Node;
bool insert(const pair<key,value>& kv)
{
Node* newnode = new Node(kv);
if (_root == nullptr)
{
_root = newnode;
return true;
}
Node* cur = _root;
Node* parent = _root;
while (cur != nullptr)
{
if (newnode->_kv.first < cur->_kv.first)
{
parent = cur;
cur = cur->_left;
}
else if (newnode->_kv.first > cur->_kv.first)
{
parent = cur;
cur = cur->_right;
}
else
{
return false;
}
}
if (newnode->_kv.first > parent->_kv.first)
parent->_right = newnode;
else
parent->_left = newnode;
return true;
}
bool find(const key& key)
{
Node* cur = _root;
while (cur != nullptr)
{
if (key < cur->_kv.first)
cur = cur->_left;
else if (key > cur->_kv.first)
cur = cur->_right;
else
return true;
}
return false;
}
void inorder()
{
_inorder(_root);
}
bool erase(const key& key)
{
assert(_root!=nullptr);
Node* cur = _root;
Node* parent = _root;
while (cur != nullptr)
{
if (key < cur->_kv.first)
{
parent = cur;
cur = cur->_left;
}
else if (key > cur->_kv.first)
{
parent = cur;
cur = cur->_right;
}
else//找到节点并删除,待删除节点为cur
{
if (_root->_left==nullptr&&_root->_right==nullptr)
{
delete _root;
_root = nullptr;
return true;
}
if (cur->_left == nullptr)
{
if (parent->_left == cur)
{
parent->_left = cur->_right;
}
else
{
parent->_right = cur->_right;
}
}
else if (cur->_right == nullptr)
{
if (parent->_left == cur)
{
parent->_left = cur->_left;
}
else
{
parent->_right = cur->_left;
}
}
else
{
//找到右子树的最小节点
Node* rightmin = cur->_right;
Node* rightminp = cur;
while (rightmin->_left != nullptr)
{
rightminp = rightmin;
rightmin = rightmin->_left;
}
cur->_kv = rightmin->_kv;
if (rightminp->_left != rightmin)
{
rightminp->_right = rightmin->_right;
}
else
{
rightminp->_left = rightmin->_right;
}
delete rightmin;
return true;
}
delete cur;
return true;
}
}
}
private:
void _inorder(Node* root)
{
if (root == nullptr)
return;
_inorder(root->_left);
cout << root->_kv.second << " ";
_inorder(root->_right);
}
Node* _root;
};