目录
1.红黑树
1.1红黑树的概念
1.2红黑树的性质
1.3红黑树节点的定义
1.4红黑树的插入操作
1.5红黑树的验证
1.6红黑树的删除
1.7红黑树与AVL树的比较
1.8红黑树的应用
1.红黑树
1.1红黑树的概念
红黑树,是一种二叉搜索树,但在每个结点上增加一个存储位表示结点的颜色,可以是Red或 Black。 通过对任何一条从根到叶子的路径上各个结点着色方式的限制,红黑树确保没有一条路径会比其他路径长出俩倍,因而是接近平衡的。
1.2红黑树的性质
1. 每个结点不是红色就是黑色
2. 根节点是黑色的
3. 如果一个节点是红色的,则它的两个孩子结点是黑色的
4. 对于每个结点,从该结点到其所有后代叶结点的简单路径上,均包含相同数目的黑色结点
5. 每个叶子结点都是黑色的(此处的叶子结点指的是空结点)
1.3红黑树节点的定义
我们将红色与黑色设置成枚举类型,使代码看起来更加规范,我们定义节点采用类模板的方式,内部成员分别是左节点指针,右节点指针,父亲节点指针,pair结构体类型的变量,然后就是代表我们颜色的变量。我们再对它们进行初始化列表就可以了,我们的每个节点初始颜色都得设置成红色,不然就无法满足我们上面给的5条红黑树的性质。
1.4红黑树的插入操作
红黑树是在二叉搜索树的基础上加上其平衡限制条件,因此红黑树的插入可分为两步:
1. 按照二叉搜索的树规则插入新节点
2. 检测新节点插入后,红黑树的性质是否造到破坏
因为新节点的默认颜色是红色,因此:如果其双亲节点的颜色是黑色,没有违反红黑树任何 性质,则不需要调整;但当新插入节点的双亲节点颜色为红色时,就违反了性质三不能有连 在一起的红色节点,此时需要对红黑树分情况来讨论:
约定:cur为当前节点,p为父节点,g为祖父节点,u为叔叔节点
情况一: cur为红,p为红,g为黑,u存在且为红
cur和p均为红,违反了性质三,此处能否将p直接改为黑?——不能
解决方式:将p,u改为黑,g改为红,然后把g当成cur,继续向上调整。
情况二: cur为红,p为红,g为黑,u不存在/u存在且为黑
在我们搞清楚了插入的操做的原理之后,我们再来看它的代码就很容易明白了。
//插入 bool Insert(const pair<K, value>& kv) { if (_root == nullptr) { _root = new Node(kv); _root->_col = BLACK; return true; } Node* parent = nullptr; Node* cur = _root; while (cur) { if (kv.first > cur->_kv.first) { parent = cur; cur = cur->_right; } else if (kv.first < cur->_kv.first) { parent = cur; cur = cur->_left; } else { return false; } } cur = new Node(kv); cur->_col = RED; if (kv.first < parent->_kv.first) { parent->_left = cur; } else { parent->_right = cur; } cur->_parent = parent; //调整红黑树 //parent是黑的也直接结束 while (parent && parent->_col == RED) { //关键看叔叔 Node* grandf = parent->_parent; if (parent == grandf->_left) { Node* uncle = grandf->_right; //叔叔存在且为红,变色即可 if (uncle && uncle->_col == RED) { uncle->_col = parent->_col = BLACK; grandf->_col = RED; //继续往上处理 cur = grandf; parent = cur->_parent; } else//叔叔不存在,或则存在且为黑 { // g // p u //c if (cur == parent->_left) { parent->_col = BLACK; grandf->_col = RED; RotateR(grandf); } // g // p u // c else { RotateL(parent); grandf->_col = RED; cur->_col = BLACK; RotateR(grandf); } break; } } else { Node* uncle = grandf->_left; //叔叔存在且为红,变色即可 if (uncle && uncle->_col == RED) { uncle->_col = parent->_col = BLACK; grandf->_col = RED; //继续往上处理 cur = grandf; parent = cur->_parent; } else//叔叔不存在,或则存在且为黑 { // g // u p // c if (cur == parent->_right) { parent->_col = BLACK; grandf->_col = RED; RotateL(grandf); } // g // u p // c else { RotateR(parent); grandf->_col = RED; cur->_col = BLACK; RotateL(grandf); } break; } } } _root->_col = BLACK; return true; }看过我AVL树或则二叉搜索树文章的同学肯定对前半部分代码非常熟悉了,就是二叉搜索树的方式进行插入,接下来我们直接分析红黑树的调整部分的代码。
我们可以看到我们循环的条件是父亲节点不为空且是红的就要一直进行调整,根据我们所画的图,我们需要一个祖父节点,我们发现接下来是有一套if...else,这是判断父亲节点是祖父的左孩子还是右孩子,方便我们确定叔叔节点的位置,我们所画的图只是if的情况,else的情况我没有画的原因是只要你把if的逻辑弄懂了,那么else就是反一下,没有什么新的东西,我等会稍微讲一讲就清楚了,我们重新回到if里,这种情况,叔叔节点就是祖父的右孩子,按照情况一,叔叔存在且为红,那么我们只需要进行变色操作就可以了,如果叔叔不存在,或则存在且为黑,那么我们就需要进行旋转操作,按照情况二的图里,如果cur是在父亲的左子树,那么直接右旋就可以了,不要忘了父亲节点和祖父节点要变色,如果cur是在父亲的右子树方向,那么我们就要进行左旋,变色,再右旋就可以了,跟我们画的图的思路是一模一样的。有了这个思路再看我们else的代码就会发现除了把旋转方向对换一下,指针方向稍微改改,其他可以说是一模一样。
旋转代码:
//右旋 void RotateR(Node* parent) { Node* SubL = parent->_left; Node* SubLR = SubL->_right; parent->_left = SubLR; if (SubLR) { SubLR->_parent = parent; } SubL->_right = parent; Node* ppnode = parent->_parent; parent->_parent = SubL; if (parent == _root) { _root = SubL; _root->_parent = nullptr; } else { if (ppnode->_left == parent) { ppnode->_left = SubL; } else if (ppnode->_right == parent) { ppnode->_right = SubL; } SubL->_parent = ppnode; } }//左旋 void RotateL(Node* parent) { Node* SubR = parent->_right; Node* SubRL = SubR->_left; parent->_right = SubRL; if (SubRL) { SubRL->_parent = parent; } SubR->_left = parent; Node* ppnode = parent->_parent; parent->_parent = SubR; if (parent == _root) { _root = SubR; _root->_parent = nullptr; } else { if (ppnode->_left == parent) { ppnode->_left = SubR; } else if (ppnode->_right == parent) { ppnode->_right = SubR; } SubR->_parent = ppnode; } }右旋和左旋的代码讲解大家可以去看我的C++实现——AVL树那篇文章,这里的左旋右旋代码跟那里的是一模一样的,只不过少了行平衡因子的更新而已,因为红黑树不用平衡因子。
1.5红黑树的验证
红黑树的检测分为两步:
1. 检测其是否满足二叉搜索树(中序遍历是否为有序序列)
2. 检测其是否满足红黑树的性质
中序遍历代码:
//中序遍历 void InOrder() { _InOrder(_root); } void _InOrder(Node* root) { if (root == nullptr) { return; } _InOrder(root->_left); cout << root->_kv.first<< ": " << root->_kv.second << endl; _InOrder(root->_right); }中序遍历就不用我多说什么了吧,就是按照左根右的方式进行递归就可以了。
判断是否是红黑树:
//判断是否平衡 bool IsBalance() { if (_root->_col == RED) { return false; } int refNum = 0; Node* cur = _root; while (cur) { if (cur->_col == BLACK) { refNum++; } cur = cur->_left; } return Check(_root, 0, refNum); } bool Check(Node* root, int blacknum,const int refnum) { if (root == nullptr) { if (refnum != blacknum) { cout << "存在黑色节点不相等的路径" << endl; return false; } return true; } if (root->_col == RED && root->_parent->_col == RED) { cout << root->_kv.first << ": " << "存在红色连续" << endl; return false; } if (root->_col == BLACK) { blacknum++; } return Check(root->_left, blacknum, refnum) && Check(root->_right, blacknum, refnum); }判断是否是红黑树我们要按照它的5条性质去设计。
首先,判断根节点是不是黑的,不是直接返回false,接下来我们再来看其它性质是否满足,我们先计算出一条路径,然后交给check函数去做。
当一条路走完后,我们看一下黑色是不是一样多,一样多我们就返回true,否则返回false。我们还要看是否有连续的红色存在,有就返回false。
最后就是以递归的方式遍历每条路径,遇到黑色节点记录上就好了。
1.6红黑树的删除
红黑树的删除本节不做讲解,有兴趣的同学可参考:《算法导论》或者《STL源码剖析》
推荐博客:http://www.cnblogs.com/fornever/archive/2011/12/02/2270692.html
1.7红黑树与AVL树的比较
红黑树和AVL树都是高效的平衡二叉树,增删改查的时间复杂度都是O(log_2 N),红黑树不追求绝对平衡,其只需保证最长路径不超过最短路径的2倍,相对而言,降低了插入和旋转的次数, 所以在经常进行增删的结构中性能比AVL树更优,而且红黑树实现比较简单,所以实际运用中红黑树更多。
1.8红黑树的应用
1. C++ STL库 -- map/set、mutil_map/mutil_set
2. Java 库
3. linux内核
4. 其他一些库
C++实现——红黑树
news2026/2/14 0:48:08
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.coloradmin.cn/o/2056913.html
如若内容造成侵权/违法违规/事实不符,请联系多彩编程网进行投诉反馈,一经查实,立即删除!相关文章
失易得数据恢复体验,2024精选数据恢复工具推荐!
数据丢失的风险无处不在,可能是由于硬件故障、软件错误、病毒感染或人为操作失误等原因。在这种情况下,数据恢复工具就显得尤为重要。本文将介绍几款市场上广受好评的数据恢复工具,帮助您在数据丢失后能够迅速找回宝贵的信息。
一、Foxit数据…
Windows客户端加入域环境时提示指定的服务器无法运行请求的操作
工作中小毛小病之:如下图 问题出在域控制器上,检查域控制器的各项域服务是否正常,确认windows防火墙关闭,一般能解决这个问题;
如果之前一切正常,只是某台电脑重装系统或者新电脑加入域出现这个情况&#…
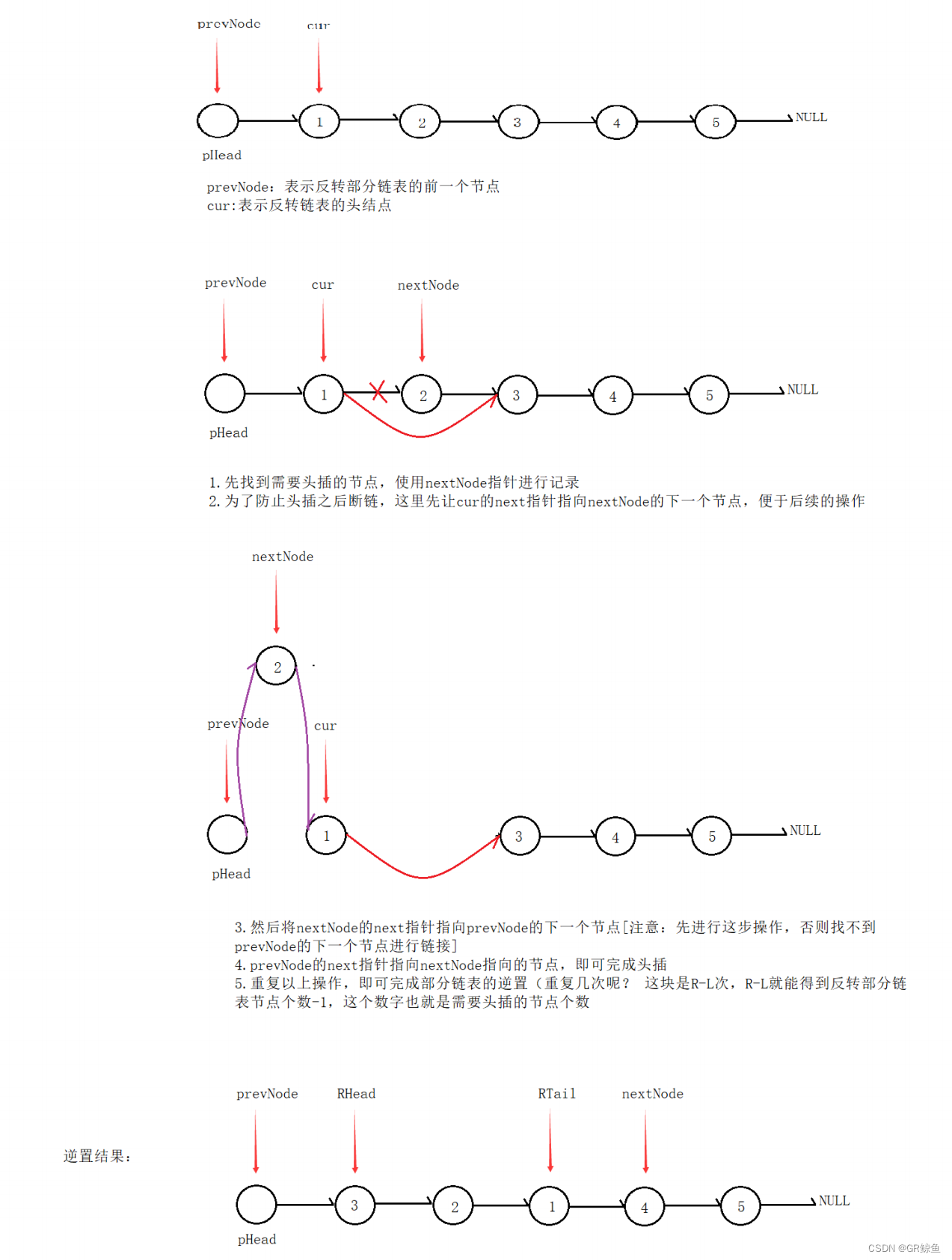
每日OJ_牛客_反转部分单向链表
目录
牛客_反转部分单向链表
解析代码 牛客_反转部分单向链表
反转部分单向链表__牛客网 题目给的代码‘:
#include <iostream>
using namespace std;
struct Node {int val;struct Node* next;
};
Node* input_List() {int n,val;Node* pheadnew Node();…
【Java】效率工具模板的使用
Java系列文章目录
补充内容 Windows通过SSH连接Linux 第一章 Linux基本命令的学习与Linux历史 文章目录 Java系列文章目录一、前言二、学习内容:三、问题描述四、解决方案:4.1 乱码问题4.2 快捷键模板4.3 文件模板 一、前言
提高效率
二、学习内容&am…
【开端】Linux抓包测试接口
一、绪论 平时我们开发接口,可以通过程序去调用接口测试接口的情况,也可以通过postman去测试接口的联通情况,也可以直接通过命令去调试接口的情况。 二、几种接口调试方式
1、程序代码测试 public static void main(String[] args) {String …
电子木鱼+提肛+游戏地图,车机还能这么玩?
文/王俣祺 导语:电子木鱼、提肛训练、游戏级地图,你很难想象这些“直男关怀”是来自小鹏MONA M03的车机系统。最近,一批关于MONA M03车机功能的视频在网上疯传,一系列“没用但有趣”的功能广受年轻用户的好评,情绪价值…
【Linux】搭建Openstack(一)
搭建openstack平台的总结
Openstack是一个开源的云计算平台,可以提供基础设施即服务(IaaS)的功能,让用户可以在自己的数据中心部署和管理虚拟化的资源。
Openstack是当今最具影响力的云计算管理工具——通过命令或者基于web的可…
PostgreSQL下载、安装(Windows 10/11 64位)详细教程【超详细,保姆级教程!!!】
本文介绍关于windows 11如何下载、安装PostgreSQL-15.8版本的详细步骤
一、下载PostgreSQL
1、进入官网 PostgreSQL下载地址(官网)
直达PostgreSQL下载页面(官网)
2、点击“Download the installer”链接,选择合适…
使用Seaborn绘制热力图
热力图是一种用于展示矩阵数据的图表,其中颜色深浅表示数据值的大小。
import seaborn as sns
import numpy as np
import matplotlib.pyplot as plt # 创建示例数据
data np.random.rand(10, 12) # 绘制热力图
sns.heatmap(data, annotTrue, cmapcoolwa…
Ubuntu20.04离线安装 Docker
1.下载3个docker离线安装包,下载网址:
https://download.docker.com/linux/ubuntu/dists/xenial/pool/stable/amd64/2.把3个离线安装包拷贝到ubuntu本地执行以下命令
sudo dpkg -i containerd.io_1.4.6-1_amd64.deb
sudo dpkg -i docker-ce-cli_20.10.…
蓝队技能-应急响应篇C2后门权限维持手法WindowsLinux基线检查排查封锁清理
知识点
1、应急响应-C2后门-排查&封锁
2、应急响应-权限维持-排查&清理
3、应急响应-基线检测-整改&排查演示案例-蓝队技能-C2后门&权限维持-基线检查&查杀封锁-Windows
1、常规C2后门-分析检测
无隐匿手法 也可以把怀疑的exe程序上传到沙箱上分析
有…
Java二十三种设计模式-中介者模式(22/23)
本文深入探讨了中介者模式,这是一种行为型设计模式,通过定义一个中介者对象来简化对象间的通信,降低耦合度,并提高系统的模块化,同时提供了实现示例、使用场景、优缺点分析、与其他设计模式的比较,以及最佳…
java中final的使用方法
package Test;/*** author gyf* ClassName Test* Date 2024/8/13 16:26* Version V1.0* Description :*/
public class Test {public static void main(String[] args) {// 被final修饰就不能修改变量了final int a 10;System.out.println(a);}
}
// 若父类用final 修饰 则子类…
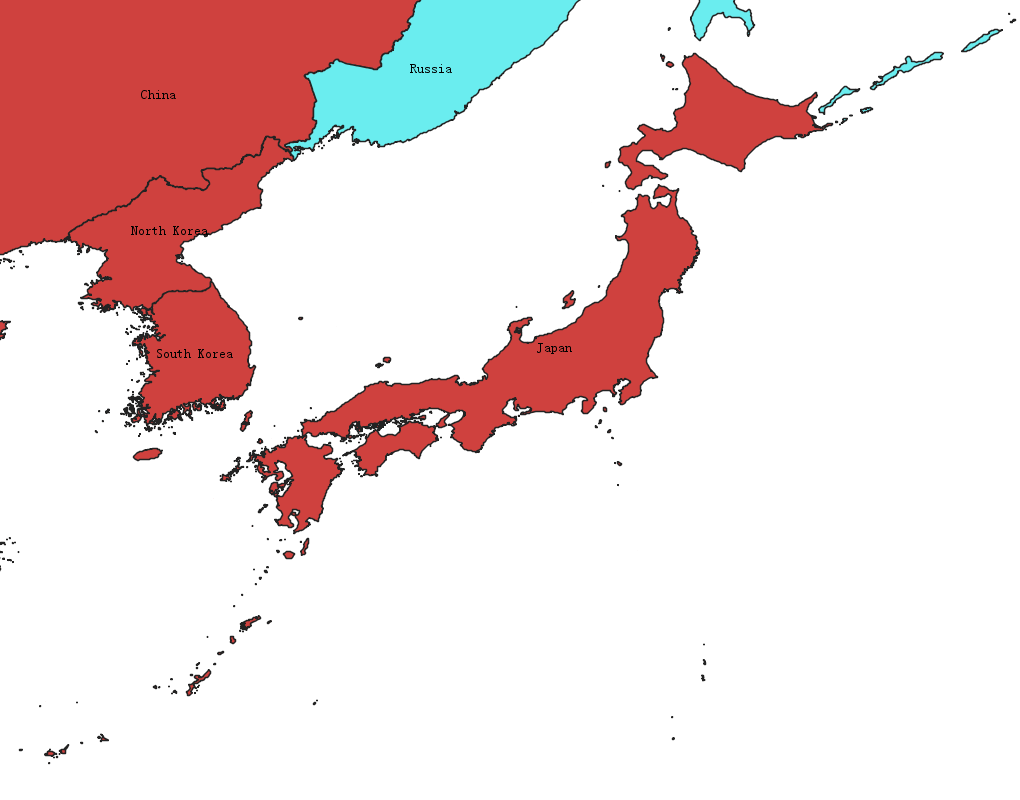
基于Java和GeoTools的Shapefile矢量数据缩略图生成实践
目录 前言
一、关于GeoTools的图片生成
1、关于GtRenderer
2、关于 图像生成架构
3、流式计算绘制
二、全球空间预览生成实战
1、pom.xml中关于图像生成依赖
2、样式设置及地图资源绑定
3、图片生成绘制
4、图片生成测试
三、成果验证
1、全球范围生成
2、我国的范…
快速批量替换图片名称为指定名称(附代码)
目录 一、需求二、代码使用方法三、代码四、效果展示 一、需求
深度学习配对训练,有时配对图像的名称需要一致,这里写了一个脚本,快速批量替换图片名称中某些字符串。
二、代码使用方法
使用代码时需要修改的地方见下: 三、代码…