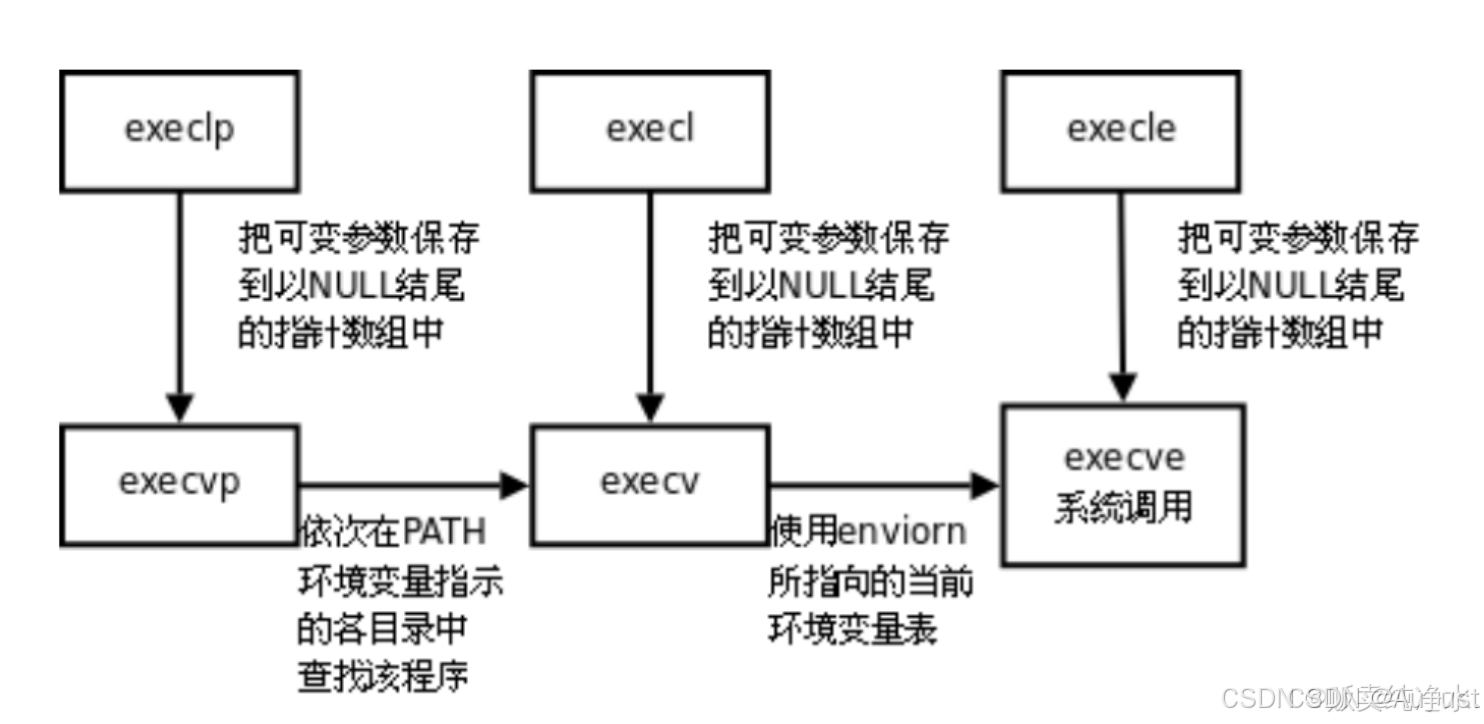
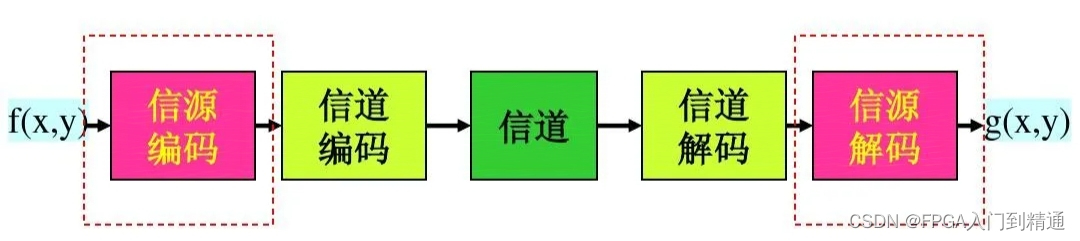
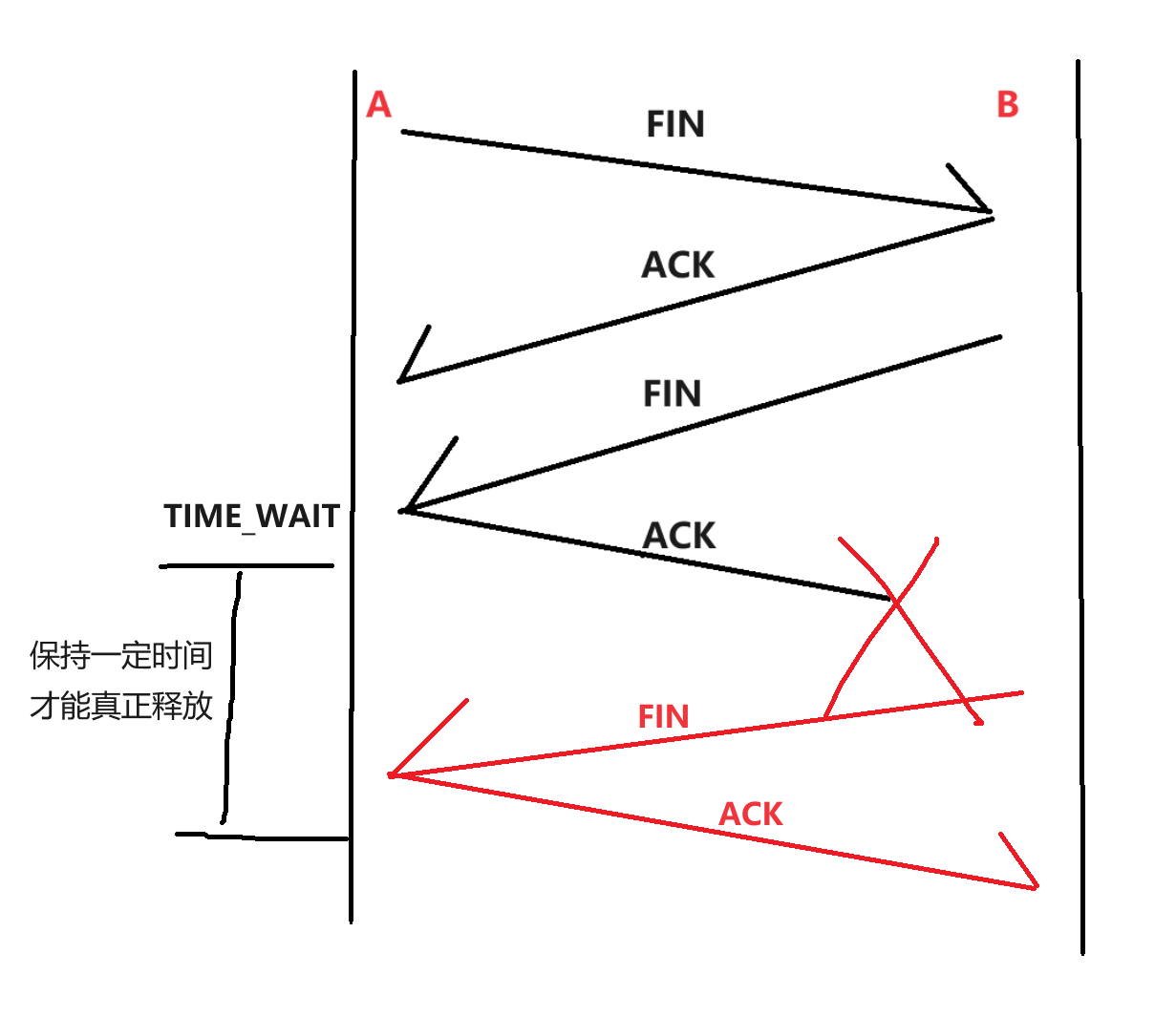
放大器
放大器的输出信号是直流源和信号源经过放大器后,共同的作用,缺一不可。
直流参数
与放大器中电压源部分有关的参数,即放大器的直流参数。
- 采用直流电压源供电,电源电压是恒定的,但是电压源的输出电流是变化量。
- 在考虑功率时,需要将电流平均以后乘以电压得到平均功率。电源的平均功率才是实际被消耗掉的功率,又称为有功功率。
交流参数
与放大器中信号部分有关的参数,即放大器的交流参数。
放大倍数
A
u
=
u
o
u
i
A
u
i
=
u
o
i
i
A
i
=
i
o
i
i
A
i
u
=
i
o
i
i
A_u=\frac{u_o}{u_i} \\ A_{ui}=\frac{u_o}{i_i}\\ A_{i}=\frac{i_o}{i_i}\\ A_{iu}=\frac{i_o}{i_i}
Au=uiuoAui=iiuoAi=iiioAiu=iiio
最常用的放大倍数是
A
u
A_u
Au。
源电压放大倍数 A u s A_{\mathrm{us}} Aus
A
u
s
=
u
o
u
s
A_{\mathrm{us}}=\frac{u_{\mathrm{o}}}{u_{\text{s}}}
Aus=usuo
相量表示
放大倍数的比值定义在正弦量的计算时,一般采用相量分析:
- 幅值( ∣ A ∣ |A| ∣A∣):表示输出信号比输入信号在大小上增大的倍数。
- 相角(
∠
A
\angle A
∠A):表示输出信号与输入信号的相位差。
频率响应
放大倍数并非恒定值,不同的频率是不一样的。交流参数包含中频段动态参数和全频段频率响应。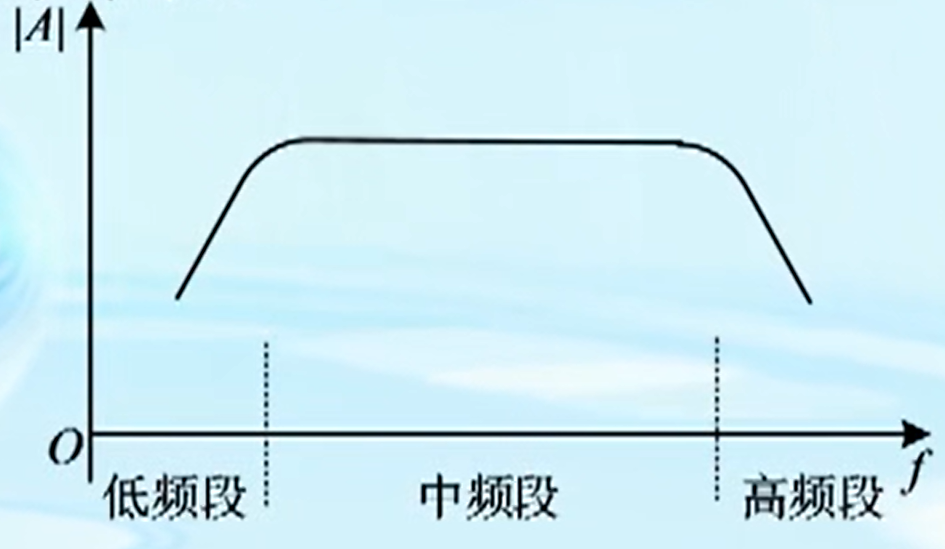
中频段
放大倍数在中间一段频率内几乎不变,这段频率称为中频段: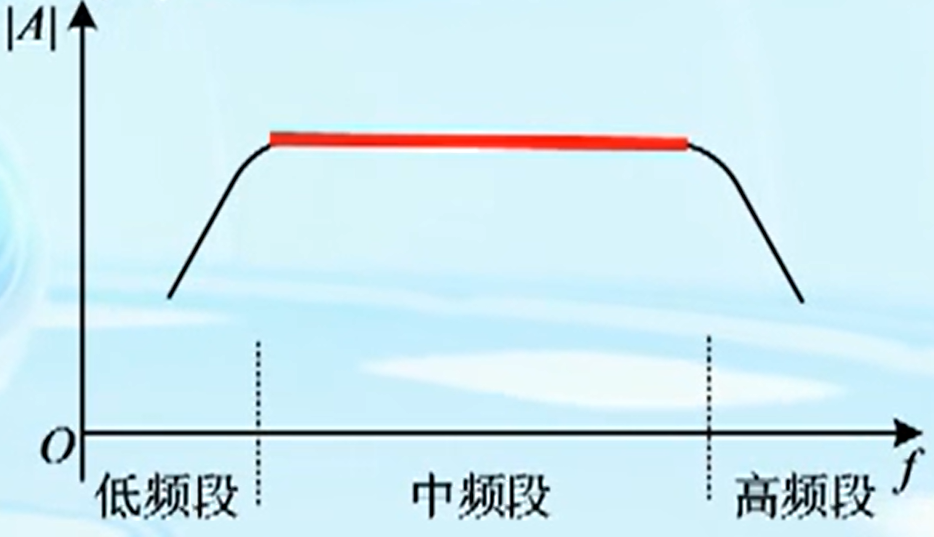
低频段
随着频率降低,放大倍数
∣
A
∣
|A|
∣A∣下降。
高频段
随着频率升高,放大倍数
∣
A
∣
|A|
∣A∣下降。
中频段动态参数(通带电压放大倍数 A up A_{\text{up}} Aup)
在低频模拟电路中的中频段,放大倍数的幅值与频率几乎没有关系,用通带电压放大倍数
A
up
A_{\text{up}}
Aup来表示,
A
up
A_{\text{up}}
Aup仍为复数。
对于低频模拟电路而言,如果考虑输出信号和输入信号的相位差,只会有两种情况:
∠
A
=
0
°
\angle A=0°
∠A=0°(同相)或
∠
A
=
180
°
\angle A=180°
∠A=180°(反相)。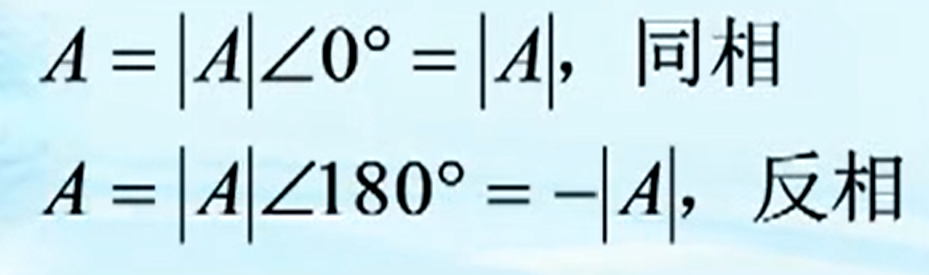
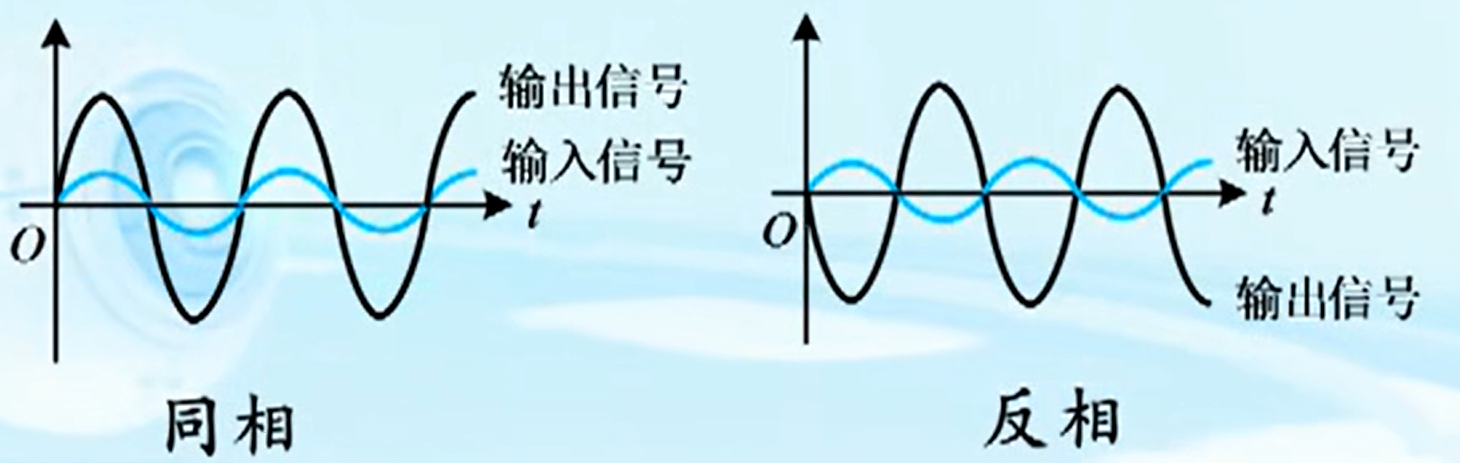
同相放大
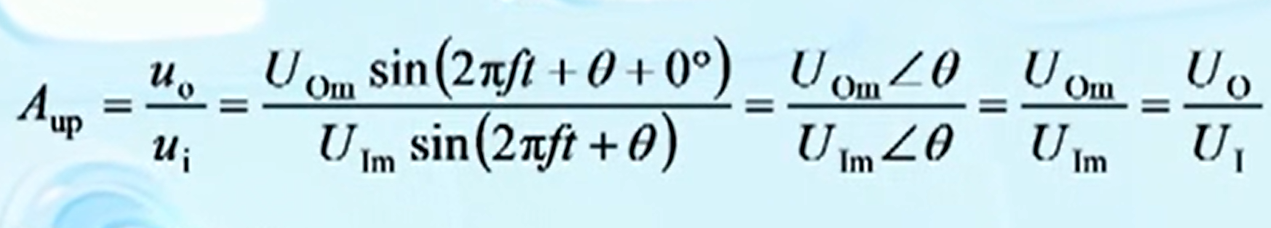
反相放大
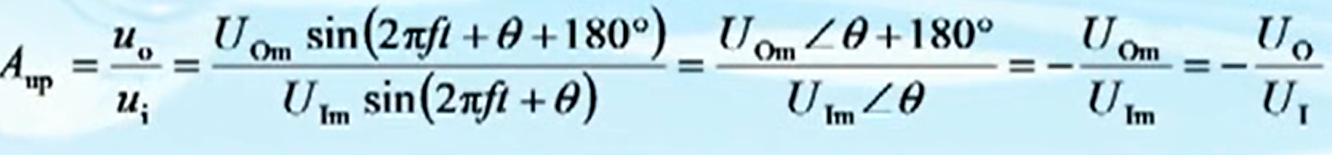
输入电阻
以电压放大器为例,放大器的输入信号并非简单等于信号源的开路电压
u
s
u_{\text{s}}
us。如果将放大器整体作为信号源的负载被等效成一个电阻,则称为输入电阻(
R
i
R_{\mathrm{i}}
Ri)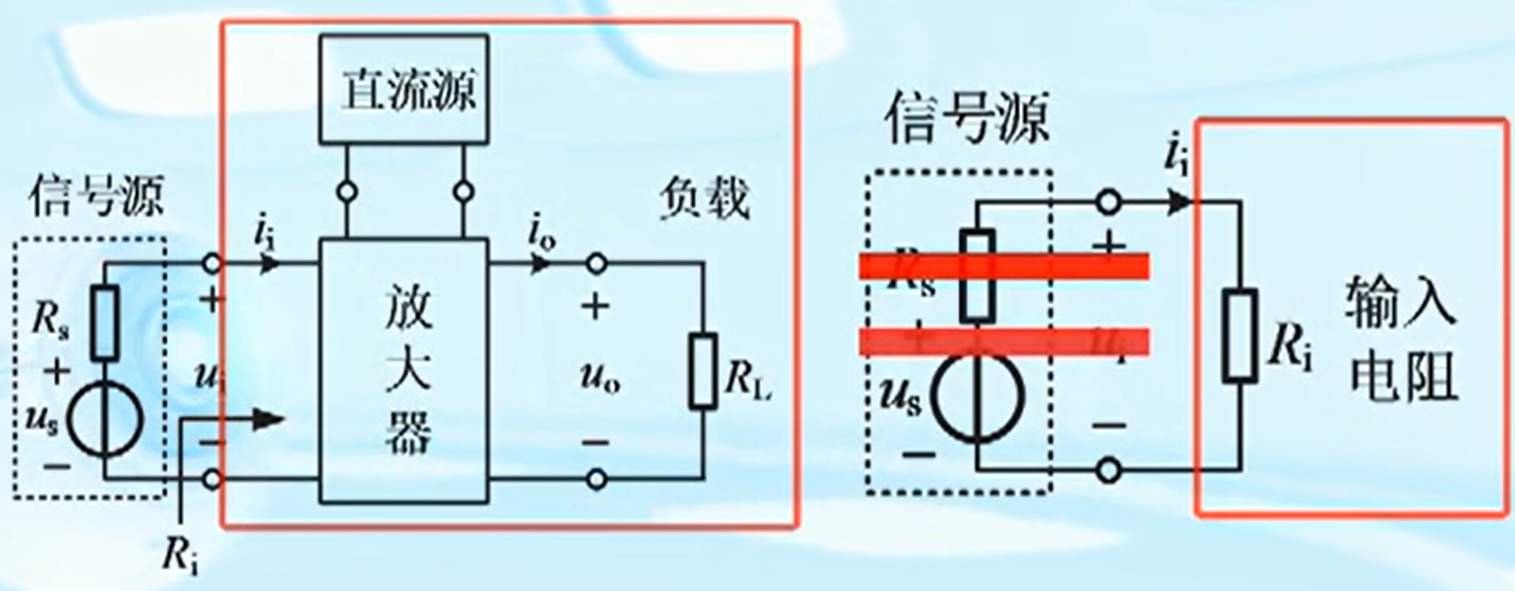
信号源开路电压 u s u_{\mathrm{s}} us、信号源内电阻 R s R_{\mathrm{s}} Rs和输入电压 u i u_{\mathrm{i}} ui之间的关系
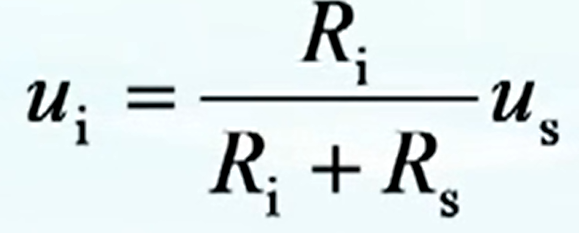
可见,
R
i
R_{\mathrm{i}}
Ri体现了放大器获取信号的能力。对于电压放大器而言,
R
i
R_{\mathrm{i}}
Ri越大,放大器输入端的
u
i
u_{\mathrm{i}}
ui越接近于源电压
u
s
u_{\mathrm{s}}
us。
R i R_{\mathrm{i}} Ri的计算方法
R
i
=
u
i
i
i
R_{\mathrm{i}}=\frac{u_{\mathrm{i}}}{i_{\mathrm{i}}}
Ri=iiui
注意,输入电阻是与放大器,直流源和负载电阻都有关的。
中频段的输入同相属性
中频段的输入电压和输入电流都是同相关系,其比值为正实数。对于低频信号的低频段和高频段,以及高频信号电路中,该比值为复数,得到的将会是输入阻抗。
输出电阻$R_{\mathrm{o
}}$
对于电压放大器而言,用输出电阻表征放大器输出电压的变化量与输出电流变化量之比。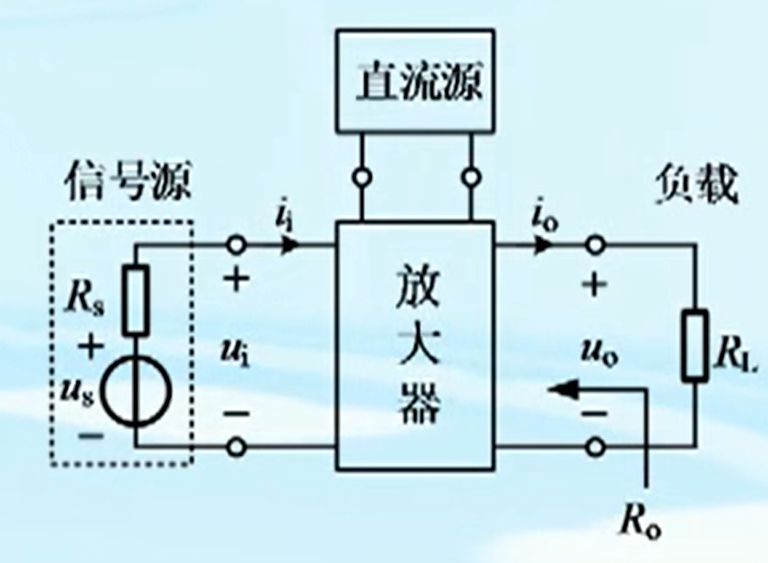
输出电阻越小,负载上获得的输出电压越高,或者说放大器的电压带负载能力越强。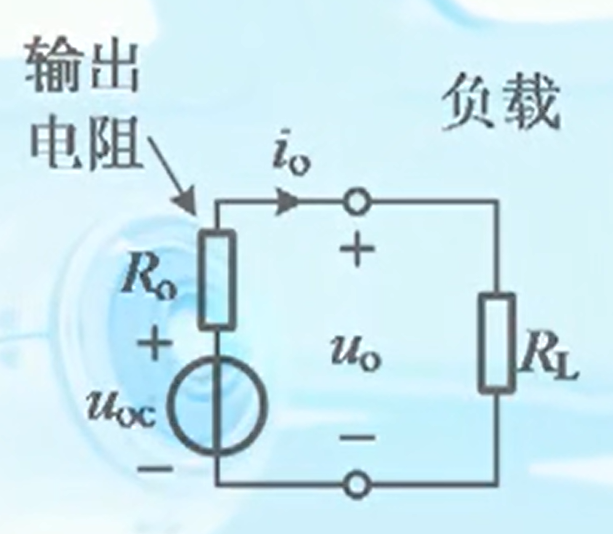
信号源、直流源和放大器的戴维宁等效电路
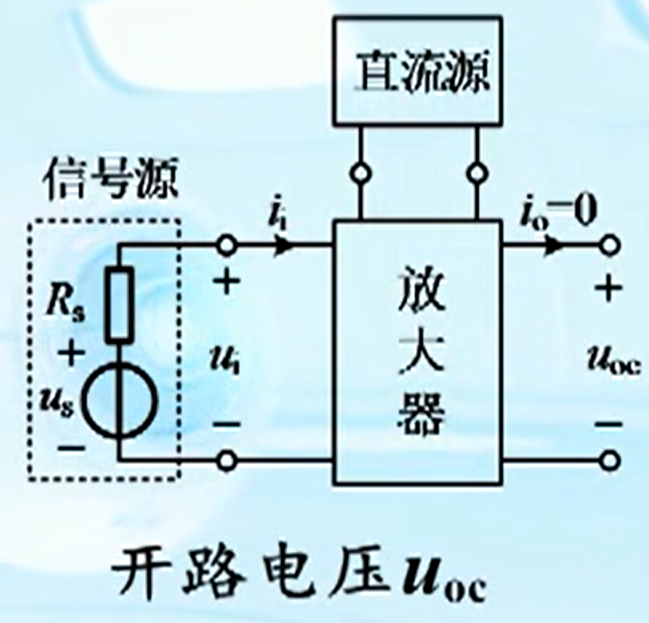
戴维宁等效电阻即为输出电阻
R
o
R_{\mathrm{o}}
Ro,在高频电路中称为输出阻抗。
分析输出电阻的方法
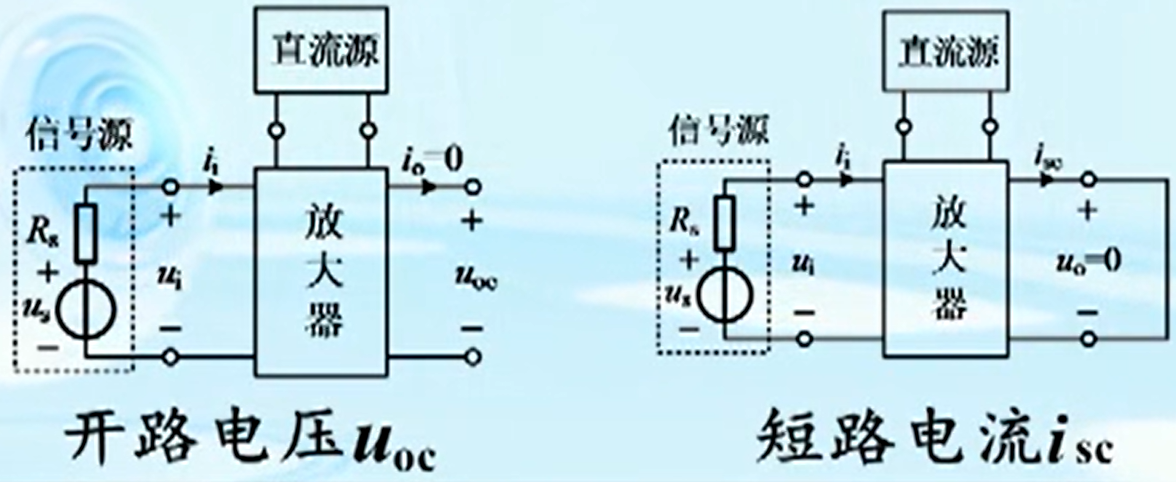
R
o
=
u
o
c
i
s
c
R_{\mathrm{o}}=\frac{u_{\mathrm{oc}}}{i_{\mathrm{sc}}}
Ro=iscuoc
如果实际的放大电路不允许端口开路或短路,则不可直接测量开路电压和短路电流的,替代的方法是将负载电阻
R
L
R_{\mathrm{L}}
RL略微改变,通过负载上电压的变化比负载上电流的变化,得到输出电阻。
中频段的三个重要动态参数
- 通带电压放大倍数 A u p A_{\mathrm{up }} Aup
- 输入电阻 R i R_{\mathrm{i}} Ri
- 输出电阻
R
o
R_{\mathrm{o}}
Ro
全频段的频率特性
全频段的频率特性包括幅度随频率变化的幅频特性和相位随频率变化的相频特性。
中频段与低频段、高频段的分界线
一般工程应用中,将放大倍数的幅值下降到中频段
∣
A
up
∣
|A_{\text{up}}|
∣Aup∣的
1
/
2
1/\sqrt{2}
1/2,即0.707倍时所对应的频率。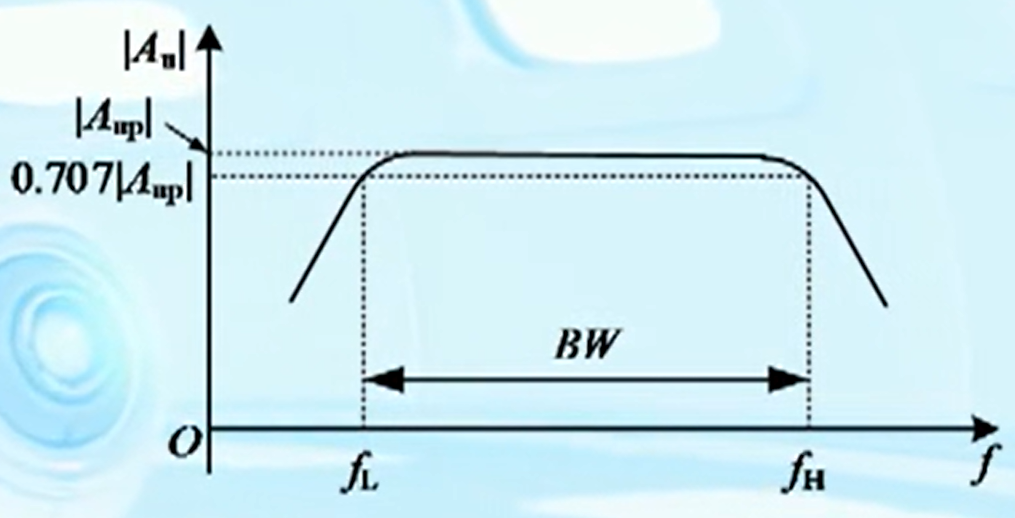
分别对应下限频率(
f
L
f_{\text{L}}
fL)和上限频率(
f
H
f_{\text{H}}
fH)。
中频段带宽 B W BW BW
B
W
=
f
H
−
f
L
BW=f_{\text{H}}-f_{\text{L}}
BW=fH−fL
放大器的直流参数和交流参数
直流参数
供电电源,包括供电电压、电流(一般指平均电流)以及平均功率等。
交流参数
主要与信号有关,包括中频段时主要考虑通带电压放大倍数、输入电阻和输出电阻以及全频段时需考虑放大器的频率响应。
放大器中频段的等效模型
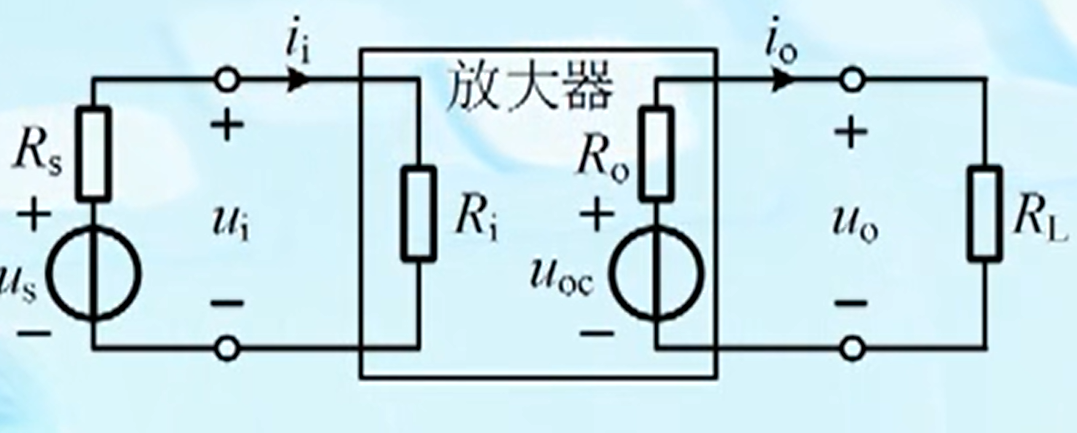
放大器与信号源构成输入回路,而与负载构成输出回路。
源电压放大倍数计算
A
us
=
u
o
u
s
=
u
o
u
i
R
i
(
R
i
+
R
s
)
=
R
i
R
i
+
R
s
u
o
u
i
=
R
i
R
i
+
R
s
A
up
A_{\text{us}}=\frac{u_{\text{o}}}{u_{\text{s}}}=\frac{u_{\text{o}}}{\frac{u_{\text{i}}}{R_{\text{i}}}(R_{\text{i}}+R_{\text{s}})}=\frac{R_{\text{i}}}{R_{\text{i}}+R_{\text{s}}}\frac{u_{\text{o}}}{u_{\text{i}}}=\frac{R_{\text{i}}}{R_{\text{i}}+R_{\text{s}}}A_{\text{up}}
Aus=usuo=Riui(Ri+Rs)uo=Ri+RsRiuiuo=Ri+RsRiAup
电流放大倍数计算
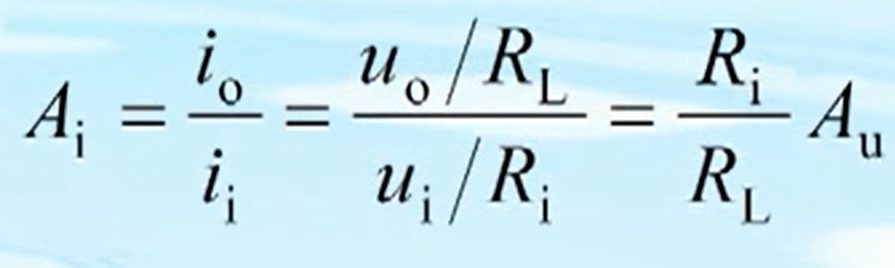
要构成实际的放大器,就必须有实际的受控源。
(全频段)电压传递函数与波特图
对放大器频率响应特性的分析
- 电压传递函数:以表达式的方式描述放大器的频率响应。
- 波特图:以图示的方式画出放大器的频率响应。
电压传递函数

体现了全频段的频率响应可以分解成通带电压放大倍数
A
up
A_{\text{up}}
Aup(与
f
f
f无关)和低频段频率响应(高通特性)和高频段频率响应(低通特性)的叠加(相乘)得到。
低频段和高频段的频率响应也是多个一阶频率响应的叠加,其中
f
Li
f_{\text{Li}}
fLi表示第
i
\text{i}
i个一阶高通的下限频率,
N
N
N是高通阶数;
f
Hk
f_{\text{Hk}}
fHk是第
k
\text{k}
k个一阶低通的上限频率,
M
M
M是低通阶数。
波特图
波特图作图原则

波特图作图法的好处
- 可以在很宽的频率范围和电压变化范围内显示结果,而不丢失细节。
- 可以采用折线来近似实际的曲线,这种折线又被称为渐近线,画折线近似图会更容易。
- 幅频特性图中,纵轴采用dB单位将线性单位中的乘/除法运算转换成dB单位中的加/减法运算。
频率临界结论
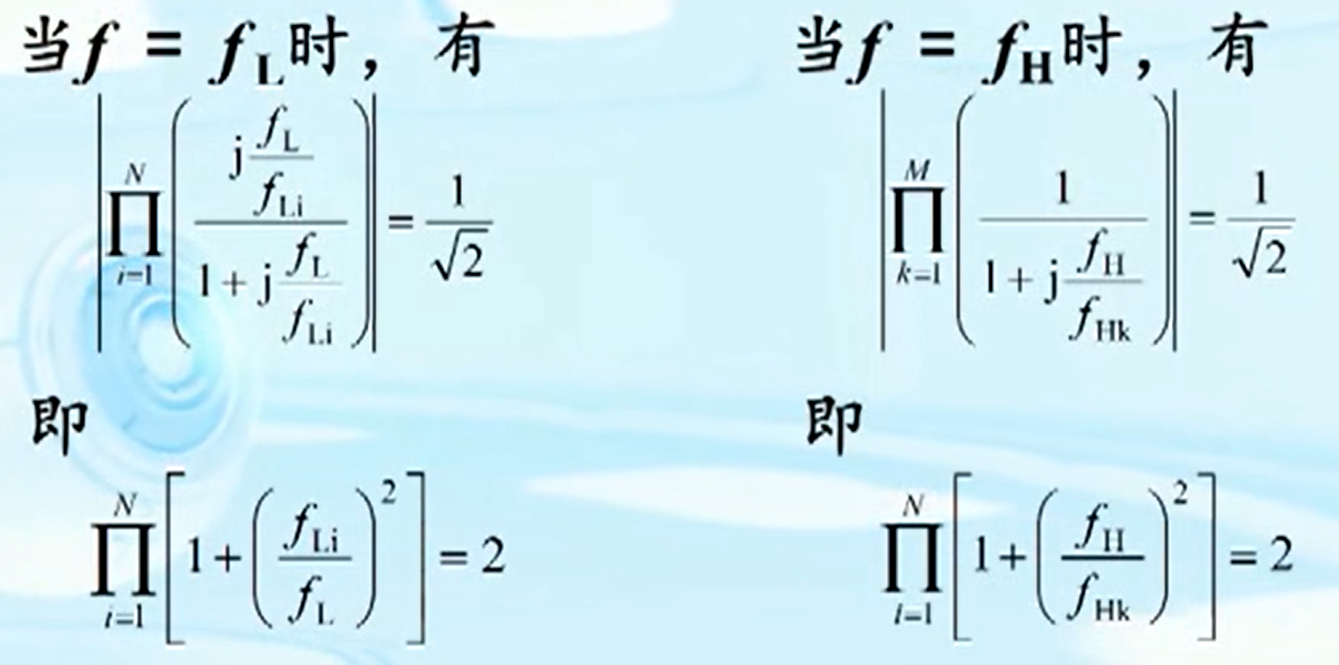
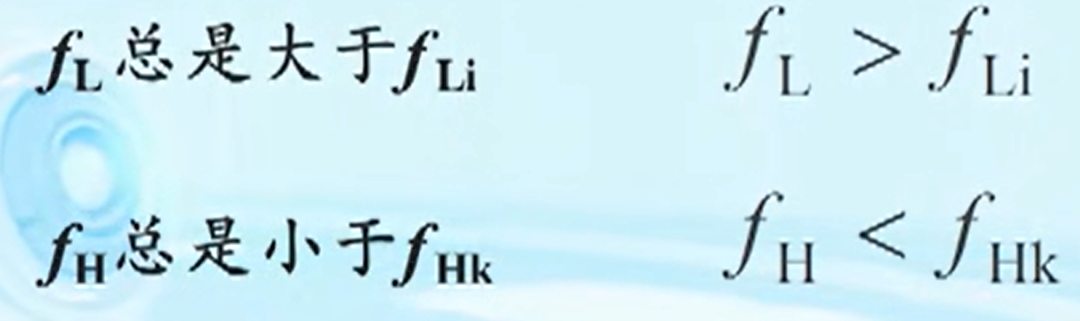
基于一阶上(下)限频率的上(下)限频率近似处理