目录
记忆化搜索
题目一:不同路径
题目二:最长递增子序列
题目三:猜数字大小II
题目四:矩阵中的最长递增路径
记忆化搜索
说到记忆化搜索,首先就需要引入斐波那契数这道题,非常经典,可以很好地说明什么是记忆化搜索
斐波那契数列
首先是列举递归的做法:
class Solution
{
public:
int fib(int n)
{
return dfs(n);
}
int dfs(int n)
{
if(n == 0 || n == 1)
return n;
return dfs(n - 1) + dfs(n - 2);
}
};这种做法非常简便,但是时间复杂度也非常高,近似于O(2^N)
而之所以慢,是因为有很多数都重复递归计算了,例如dfs(5)时,会计算dfs(4)和dfs(3),其中计算dfs(4)时,又会计算dfs(3)和dfs(2)
dfs(5)和dfs(4)都重复计算dfs(3)了,再往下看,重复计算的数更多,所以就会导致时间复杂度非常高
而如果想优化也非常简单,我们每计算出一个值,就将其放入“备忘录”中,如果后续又需要用到这个值,就不需要重复计算了,可以直接使用,所以引出记忆化搜索概念:
记忆化搜索
记忆化搜索其实就是带备忘录的递归
也就相当于递归过程中的剪枝操作了,相当于将一个指数级别的时间复杂度,变为了O(N)级别的,因为只需要计算出一次,剩下分支就可以直接使用,不会进入递归了
所以记忆化搜索的代码实现的步骤就是:
①添加一个备忘录并初始化
②递归每次返回时,将结果放入备忘录中
③每次进入递归时,查看备忘录中是否已经有结果
记忆化搜索代码如下:
class Solution
{
public:
int memo[31];
int fib(int n)
{
// 创建一个备忘录并初始化
memset(memo, -1, sizeof(memo));
return dfs(n);
}
int dfs(int n)
{
if(memo[n] != -1)
{
// 每次进入递归时,查看备忘录中是否已经有结果
return memo[n];
}
if(n == 0 || n == 1)
{
memo[n] = n; // 递归每次返回时,将结果放入备忘录中
return n;
}
// 递归每次返回时,将结果放入备忘录中
memo[n] = dfs(n - 1) + dfs(n - 2);
return memo[n];
}
};题目一:不同路径
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish” )。
问总共有多少条不同的路径?
示例 1:
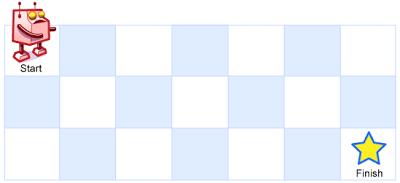
输入:m = 3, n = 7 输出:28
示例 2:
输入:m = 3, n = 2 输出:3 解释: 从左上角开始,总共有 3 条路径可以到达右下角。 1. 向右 -> 向下 -> 向下 2. 向下 -> 向下 -> 向右 3. 向下 -> 向右 -> 向下
示例 3:
输入:m = 7, n = 3 输出:28
示例 4:
输入:m = 3, n = 3 输出:6
这道题在动态规划中做过,这里使用记忆化搜索的方式解决
先想想暴力搜索的写法,再将暴力搜索改为记忆化搜索(要考虑能否改为记忆化搜索)
一、暴力搜索
class Solution
{
public:
int uniquePaths(int m, int n)
{
return dfs(m ,n);
}
int dfs(int i, int j)
{
// 两个边界条件
if(i == 0 || j == 0) return 0;
if(i == 1 && j == 1) return 1;
return dfs(i - 1, j) + dfs(i, j - 1);
}
};因为时间复杂度太高了,所以是会超时的
二、改为记忆化搜索
class Solution
{
public:
int uniquePaths(int m, int n)
{
// 添加一个备忘录并初始化
vector<vector<int>> memo(m + 1, vector<int>(n + 1));
return dfs(m ,n, memo);
}
int dfs(int i, int j, vector<vector<int>>& memo)
{
// 每次进入递归时,查看备忘录中是否已经有结果
if(memo[i][j] != 0)
{
return memo[i][j];
}
if(i == 0 || j == 0) return 0;
// 递归每次返回时,将结果放入备忘录中
if(i == 1 && j == 1)
{
memo[i][j] = 1;
return memo[i][j];
}
// 递归每次返回时,将结果放入备忘录中
memo[i][j] = dfs(i - 1, j, memo) + dfs(i, j - 1, memo);
return memo[i][j];
}
};三、改为动态规划
class Solution
{
public:
int uniquePaths(int m, int n)
{
vector<vector<int>> dp(m + 1, vector<int>(n + 1));
dp[1][1] = 1;
for(int i = 1; i <= m; i++)
for(int j = 1; j <= n; j++)
{
if(i == 1 && j == 1) continue;
dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
}
return dp[m][n];
// 添加一个备忘录并初始化
// vector<vector<int>> memo(m + 1, vector<int>(n + 1));
// return dfs(m ,n, memo);
}
};题目二:最长递增子序列
给你一个整数数组 nums ,找到其中最长严格递增子序列的长度。
子序列 是由数组派生而来的序列,删除(或不删除)数组中的元素而不改变其余元素的顺序。例如,[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列
示例 1:
输入:nums = [10,9,2,5,3,7,101,18] 输出:4 解释:最长递增子序列是 [2,3,7,101],因此长度为 4 。
示例 2:
输入:nums = [0,1,0,3,2,3] 输出:4
示例 3:
输入:nums = [7,7,7,7,7,7,7] 输出:1
子序列也就是数组中不连续的序列,本题求的就是不连续的递增子序列的最大长度是多少
下面进行暴力搜索、记忆化搜索、改为动态规划三步
一、递归暴力搜索
暴力搜索就是在决策树中,首先确定子序列的起点是哪一个数,依次列举出来,第二层就是根据第一层列举出来的起点数字,从该数往后依次继续列举,直到最后一个数为止
class Solution
{
public:
int ret;
int lengthOfLIS(vector<int>& nums)
{
for(int i = 0; i < nums.size(); i++)
ret = max(ret, dfs(nums, i));
return ret;
}
int dfs(vector<int>& nums, int pos)
{
// 寻找该数字后面的最长子序列,需要加上该数字,所以初始化为1
int ret = 1;
for(int i = pos + 1; i < nums.size(); i++)
{
// 符合条件再递归
if(nums[i] > nums[pos])
ret = max(ret, dfs(nums, i) + 1);
}
return ret;
}
};本题的暴力搜索同样会超时
二、记忆化搜索
class Solution
{
public:
int ret;
int lengthOfLIS(vector<int>& nums)
{
// 添加一个备忘录并初始化
int n = nums.size();
vector<int> memo(n);
// 哪个位置为最长子序列的起点不确定,所以每个位置都寻找一次
for(int i = 0; i < n; i++)
ret = max(ret, dfs(nums, i, memo));
return ret;
}
int dfs(vector<int>& nums, int pos, vector<int>& memo)
{
// 每次进入递归时,查看备忘录中是否已经有结果
if(memo[pos] != 0) return memo[pos];
// 寻找该数字后面的最长子序列,需要加上该数字,所以初始化为1
int ret = 1;
for(int i = pos + 1; i < nums.size(); i++)
{
// 符合条件再递归
if(nums[i] > nums[pos])
ret = max(ret, dfs(nums, i, memo) + 1);
}
// 递归每次返回时,将结果放入备忘录中
memo[pos] = ret;
return memo[pos];
}
};加上备忘录后,就能运行通过,不会超时了
三、改为动态规划
因为本题也有相同的子问题,会重复计算,例如选择第一个数字作为子序列起点时,会递归到第二个数字,此时就会与初始选择第二个数字做起点重复计算
这里的动态规划版本与动态规划章节里的方式不同,因为此题的动态规划版本是依据记忆化搜索的版本做的改变
因为记忆化搜索中,想知道该位置为起点的最长子序列,需要知道该位置之后的最长子序列,所以是从后向前的
dfs与dp是对应的
class Solution
{
public:
int lengthOfLIS(vector<int>& nums)
{
int n = nums.size(), ret = 0;
// 与记忆化搜索相同,初始化为1
vector<int> dp(n, 1);
// 从后向前
for(int i = n - 1; i >= 0; i--)
{
for(int j = i + 1; j < n; j++)
{
if(nums[j] > nums[i])
dp[i] = max(dp[i], dp[j] + 1);
}
ret = max(ret, dp[i]);
}
return ret;
// 添加一个备忘录并初始化
// int n = nums.size();
// vector<int> memo(n);
// 哪个位置为最长子序列的起点不确定,所以每个位置都寻找一次
// for(int i = 0; i < n; i++)
// ret = max(ret, dfs(nums, i, memo));
// return ret;
}
};题目三:猜数字大小II
我们正在玩一个猜数游戏,游戏规则如下:
- 我从
1到n之间选择一个数字。 - 你来猜我选了哪个数字。
- 如果你猜到正确的数字,就会 赢得游戏 。
- 如果你猜错了,那么我会告诉你,我选的数字比你的 更大或者更小 ,并且你需要继续猜数。
- 每当你猜了数字
x并且猜错了的时候,你需要支付金额为x的现金。如果你花光了钱,就会 输掉游戏 。
给你一个特定的数字 n ,返回能够 确保你获胜 的最小现金数,不管我选择那个数字 。
猜数字我们都玩过,这道题与传统猜数字不同的是,如果猜错需要支付当前猜的数字的钱
题目要求我们计算出在某一种选择策略中,无论选择的是数字几,都能确保获胜所花的现金数能够获胜,求这些策略中需要的最小的现金数
所以第一步,先考虑暴力搜索怎么做
第一步确定需要选的值是多少,假设该数在 1 ~ 10 之间,此时如果选择 i
那么可能 i 比所需要的数小,也可能比所需要的数大,所以决策树向左延伸就是 1 ~ i - 1
向右延伸就是 i + 1 ~ 10
由于需要的就是满足条件的最小值,所以在 i 下面扩展的 1 ~ i - 1 与 i + 1 ~ 10中,需要选择最小值向上返回,假设 1 ~ i - 1 区间返回 x,i + 1 ~ 10区间返回 y,那么最后的结果应该是
i + max(x, y),因为最终需要的结果是能够满足当前选择的任意情况,同时还需要加上当前数字的值

也就是上面这种图中,7就表示i,下一层的3和9就表示扩展的1~6和8~10之间选择的一种情况,3返回的是3 + 5 == 8,而9 返回的是 9,所以根节点7为了能够满足这两种情况,最终选择的是9,结果就是 9 + 7 == 16
一、暴力搜索的代码如下:
class Solution
{
public:
int getMoneyAmount(int n)
{
return dfs(1, n);
}
int dfs(int left, int right)
{
if(left >= right) return 0;
int ret = INT_MAX;
for(int head = left; head <= right; head++)
{
// x和y表示head下面左右分支返回上来的值
int x = dfs(left, head - 1);
int y = dfs(head + 1, right);
ret = min(ret, max(x, y) + head);
}
return ret;
}
};这种解法肯定是超时的,所以看下面的记忆化搜索代码
二、改为记忆化搜索
很简单,只需创建备忘录,再在返回时存入与进入递归时查看是否有值即可
只需要加上两行代码,就可以剪枝减掉非常多种情况,因此相比于暴力搜索的代码就不会超时了
代码如下:
class Solution
{
public:
int memo[201][201];
int getMoneyAmount(int n)
{
return dfs(1, n);
}
int dfs(int left, int right)
{
if(left >= right) return 0;
if(memo[left][right] != 0) return memo[left][right];
int ret = INT_MAX;
for(int head = left; head <= right; head++)
{
// x和y表示head下面左右分支返回上来的值
int x = dfs(left, head - 1);
int y = dfs(head + 1, right);
ret = min(ret, max(x, y) + head);
}
memo[left][right] = ret;
return memo[left][right];
}
};题目四:矩阵中的最长递增路径
给定一个 m x n 整数矩阵 matrix ,找出其中 最长递增路径 的长度。
对于每个单元格,你可以往上,下,左,右四个方向移动。 你 不能 在 对角线 方向上移动或移动到 边界外(即不允许环绕)。
示例 1:
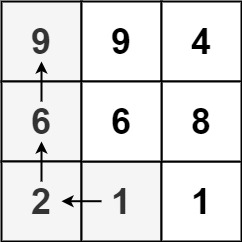
输入:matrix = [[9,9,4],[6,6,8],[2,1,1]]
输出:4
解释:最长递增路径为 [1, 2, 6, 9]。
示例 2:

输入:matrix = [[3,4,5],[3,2,6],[2,2,1]]
输出:4
解释:最长递增路径是 [3, 4, 5, 6]。注意不允许在对角线方向上移动。
示例 3:
输入:matrix = [[1]] 输出:1
本题同样需要先写出暴力解法,就是将每个位置都遍历一遍,再返回计算出的最大的值接口
肯定也会超时的,因为在暴力解法中,每一个位置可能都会计算多次
暴力搜索代码如下:
class Solution {
public:
int dx[4] = {0,0,-1,1};
int dy[4] = {-1,1,0,0};
int ret, m, n;
int longestIncreasingPath(vector<vector<int>>& matrix) {
m = matrix.size(), n = matrix[0].size();
ret = 0;
for(int i = 0; i < m; i++)
{
for(int j = 0; j < n; j++)
{
ret = max(ret, dfs(matrix, i, j));
}
}
return ret;
}
int dfs(vector<vector<int>>& matrix, int i, int j)
{
int ret = 1;
for(int k = 0; k < 4; k++)
{
int x = i + dx[k];
int y = j + dy[k];
if(x >= 0 && x < m && y >= 0 && y < n && matrix[x][y] > matrix[i][j])
{
ret = max(ret, dfs(matrix, x, y) + 1);
}
}
return ret;
}
};更新为记忆化搜索的代码,此时就不会超时了,成功解决问题:
class Solution {
public:
int dx[4] = {0,0,-1,1};
int dy[4] = {-1,1,0,0};
int ret, m, n;
int memo[201][201];
int longestIncreasingPath(vector<vector<int>>& matrix) {
m = matrix.size(), n = matrix[0].size();
ret = 0;
for(int i = 0; i < m; i++)
{
for(int j = 0; j < n; j++)
{
ret = max(ret, dfs(matrix, i, j));
}
}
return ret;
}
int dfs(vector<vector<int>>& matrix, int i, int j)
{
if(memo[i][j] != 0) return memo[i][j];
int ret = 1;
for(int k = 0; k < 4; k++)
{
int x = i + dx[k];
int y = j + dy[k];
if(x >= 0 && x < m && y >= 0 && y < n && matrix[x][y] > matrix[i][j])
{
ret = max(ret, dfs(matrix, x, y) + 1);
}
}
memo[i][j] = ret;
return memo[i][j];
}
};记忆化搜索相关题目到此结束







![[SDK]-键盘消息和鼠标消息](https://i-blog.csdnimg.cn/direct/6b5908650dc0420bab6547ee06751ec9.gif)











