目录
一、栈实现二叉树遍历的可行性
二、由递归推出栈如何实现中序遍历
1.左子树入栈
2.根结点出栈
3.右子树入栈
4.实例说明
三、代码实现
总结
一、栈实现二叉树遍历的可行性
在日撸Java三百行(day16:递归)中,我们讲过“递归”说白了就是函数自身调用自身,当递归函数调用自身时,我们可以看作是入栈的过程,调用一次就入栈一次;而当递归满足结束条件后,一层一层返回时,又可以看作是出栈的过程,返回一层就出栈一次。这样看来,递归实现和栈实现似乎是可以相互转化的,毕竟它们都满足“先进后出、后进先出”的原则。
在日撸Java三百行(day21:二叉树的深度遍历的递归实现)中,我们是利用递归的方法对二叉树进行的前中后序遍历,那么既然递归实现和栈实现可以相互转化,我们是否可以利用栈的思想来完成二叉树的遍历呢?今天我们就先从用栈实现二叉树的中序遍历开始(因为中序遍历是几种遍历中最简单的)。
二、由递归推出栈如何实现中序遍历
先来回顾一下我们之前是怎么用递归实现二叉树中序遍历的,代码如下:
/**
*********************
* In-order visit.
*********************
*/
public void inOrderVisit() {
if(leftChild != null) {
leftChild.inOrderVisit();
} // of if
System.out.print("" + value + " ");
if(rightChild != null) {
rightChild.inOrderVisit();
} // of if
} // of inOrderVisit中序遍历是按“左子树 根结点 右子树”的顺序进行遍历,上述的递归函数就是先判断当前根结点的左子树是否为空,不空则搁置当前这层函数操作,将该左子树作为新的根结点,再次调用函数;空则直接输出当前根结点,再按照同样的方法判断右子树。这个过程如果用栈来完成,可以简单概括为三步,即左子树入栈、根结点出栈、右子树入栈,下面我们就来对这三步进行分析说明。
1.左子树入栈
由上边递归函数的代码顺序可知,每次调用函数时都会优先进入左子树,如果当前左子树不空,就会进入新一层的递归函数;进入新一层的函数后,再次优先进入左子树,如果该左子树仍不空,则再次进入下一层递归函数……总结一下就是,如果左子树持续不空,那么就会一直朝着左子树的方向行进,直到某个结点的左子树为空。为了便于理解,我们以下图为例:
- 首先a作为根结点调用递归函数
- 进入a的左子树b
- a的左子树b不为空,于是将b作为新的根结点调用递归函数
- 进入b的左子树d
- b的左子树d不为空,于是将d作为新的根结点调用递归函数
- 进入d的左子树h
- d的左子树h不为空,于是将h作为新的根结点调用递归函数
- h没有左子树,停止调用

我们在一开始说过,调用一次递归函数就可以看作是入栈一次,所以上述过程,如果用栈来实现, 就是依次入栈左子树,如果该左子树中还有左子树,则继续入栈左子树,直到某个结点的左子树为空,其实也就是按照上图中红色箭头的方向持续入栈左子树。不过需要注意,每个根结点都必须在其左子树之前入栈,上图的二叉树入栈后结果如下:

2.根结点出栈
根据上面递归函数的代码,可以知道由于上图中h结点的左子树为空,所以不会继续调用函数,而是来到第11行代码直接输出h结点。这个过程反映到栈中,就是将此时的栈顶元素——h结点出栈并访问它。
3.右子树入栈
在上述的递归函数中,输出结点h后,接下来我们就要开始判断其右子树了,如果其右子树不为空,那么就把它的右子树作为新的根结点调用递归函数。用栈的思想考虑,就是如果此时出栈元素的右子树不空,就将它的右子树入栈,然后再从该右子树出发(即把该右子树当作当前根结点),按照“左子树入栈、根结点出栈、右子树入栈”的顺序进行;而如果此时出栈元素的右子树为空,则将当前栈顶元素进行出栈,然后继续判断新出栈元素的右子树。
4.实例说明
我们简单总结一下以上三步,先将左子树依次入栈,然后出栈当前栈顶元素,再判断该出栈元素的右子树,最后根据判断结果执行。
栈实现二叉树遍历用文字语言叙述,真的既拗口又不好理解,下面我们还是用一个具体的例子来说明,这样稍微直观一点。对于下图的二叉树,栈实现中序遍历的具体步骤如下:

- 左子树依次入栈。放在这里就是将a、b、d依次入栈,由于d之后没有左子树了,所以入栈到d这里就暂时停止了。
- 将当前栈顶元素d出栈,并输出d。
- 判断此时出栈元素的右子树。由于此时出栈元素d的右子树为空,所以下一步应该将新的栈顶元素出栈。
- 将新的栈顶元素b出栈,并输出b。
- 判断此时出栈元素的右子树。由于此时出栈元素b的右子树不空,所以下一步应该将它的右子树入栈。
- 将b的右子树e入栈。(一旦右子树入栈,下一步就是该右子树的左子树依次入栈)
- 左子树再次依次入栈。放到这里就是将e之后的左子树依次入栈,由于h之后没有左子树了,所以入栈到h这里就暂时停止了。
- 将当前栈顶元素h出栈,并输出h。
- 判断此时出栈元素的右子树。由于此时出栈元素h的右子树为空,所以下一步应该将新的栈顶元素出栈。
- 将新的栈顶元素e出栈,并输出e。
- 判断此时出栈元素的右子树。由于此时出栈元素e的右子树为空,所以下一步应该将新的栈顶元素出栈。
- 将新的栈顶元素a出栈,并输出a。
- 判断此时出栈元素的右子树。由于此时出栈元素a的右子树不空,所以下一步应该将它的右子树入栈。
- 将a的右子树c入栈。(一旦右子树入栈,下一步就是该右子树的左子树依次入栈)
- 左子树再次依次入栈。放到这里就是将c之后的左子树依次入栈,由于f之后没有左子树了,所以入栈到f这里就暂时停止了。
- 将当前栈顶元素f出栈,并输出f。
- 判断此时出栈元素的右子树。由于此时出栈元素f的右子树不空,所以下一步应该将它的右子树入栈。
- 将f的右子树i入栈。(一旦右子树入栈,下一步就是该右子树的左子树依次入栈)
- 左子树再次依次入栈。但是由于此时i没有左子树了,所以这一步跳过。
- 将当前栈顶元素i出栈,并输出i。
- 判断此时出栈元素的右子树。由于此时出栈元素i的右子树为空,所以下一步应该将新的栈顶元素出栈。
- 将新的栈顶元素c出栈,并输出c。
- 判断此时出栈元素的右子树。由于此时出栈元素c的右子树不空,所以下一步应该将它的右子树入栈。
- 将c的右子树g入栈。(一旦右子树入栈,下一步就是该右子树的左子树依次入栈)
- 左子树再次依次入栈。但是由于此时g没有左子树了,所以这一步跳过。
- 将当前栈顶元素g出栈,并输出g。
- 判断此时出栈元素的右子树。由于此时出栈元素g的右子树为空,所以下一步应该将新的栈顶元素出栈。
- 将新的栈顶元素出栈。但是由于此时栈已空同时当前结点也为空,所以到此就完成了。


由这个例子,我们可以得出以下便于后续编程的结论:
- 出栈后立马输出该出栈元素
- 当栈空且结点也为空时,遍历结束
三、代码实现
大概理解这个过程之后,我们还是先开始代码模拟吧(毕竟用文字解释感觉真的不好说清楚,不过也有可能是我的语言表达水平有限吧…)
为了提高代码的复用性,这里我们重写了一个和通用性队列类似的通用性栈,代码如下:
package datastructure;
/**
*Object stack.
*
*@auther Xin Lin 3101540094@qq.com.
*/
public class ObjectStack {
/**
* The depth.
*/
public static final int MAX_DEPTH = 10;
/**
* The actual depth.
*/
int depth;
/**
* The data.
*/
Object[] data;
/**
*********************
* Construct an empty Object stack.
*********************
*/
public ObjectStack() {
depth = 0;
data = new Object[MAX_DEPTH];
} // Of the first constructor
/**
*********************
* Overrides the method claimed in Object, the superclass of any class.
*********************
*/
public String toString() {
String resultString = "";
for (int i = 0; i < depth; i++) {
resultString += data[i];
} // Of for i
return resultString;
} // Of toString
/**
*********************
* Push an element.
*
* @param paraObject The given object.
* @return Success or not.
*********************
*/
public boolean push(Object paraObject) {
if (depth == MAX_DEPTH) {
System.out.println("Stack full.");
return false;
} // Of if
data[depth] = paraObject;
depth++;
return true;
} // Of push
/**
*********************
* Pop an element.
*
* @return The object at the top of the stack.
*********************
*/
public Object pop() {
if(depth == 0) {
System.out.println("Nothing to pop.");
return '\0';
} // Of if
Object resultObject = data[depth - 1];
depth--;
return resultObject;
} // Of pop
/**
*********************
* Is the stack empty?
*
* @return True if empty.
*********************
*/
public boolean isEmpty() {
if(depth == 0) {
return true;
} // Of if
return false;
} // Of isEmpty
/**
*********************
*The entrance of the program.
*
* @param args Not used now.
*********************
*/
public static void main(String[] args) {
ObjectStack tempStack = new ObjectStack();
for(char ch = 'a'; ch < 'm'; ch++) {
tempStack.push(new Character(ch));
System.out.println("The current stack is: " + tempStack);
} // Of for ch
char tempChar;
for(int i = 0; i < 12; i++) {
tempChar = ((Character)tempStack.pop()).charValue();
System.out.println("Popped: " + tempChar);
System.out.println("The current stack is: " + tempStack);
} // Of for i
} // Of main
} // Of class ObjectStack在重写的过程中,一定要注意强制类型转换的使用。比如倒数第6行代码中,由于栈是Object类型的栈,所以得到的出栈元素肯定也是Object类型,因此我们需要使用Character先将其强制转换成Character类型,再利用charValue()方法将Character类型转换为基本数据类型char,最后再赋给同为char类型的变量tempChar。
现在我们开始创建方法,首先创建一个ObjectStack类型的对象栈,以及一个二叉树的结点引用;然后,定义一个while循环,循环条件为栈不空或者结点不空(因为栈空且结点空的时候,遍历就结束了)。
在while循环中,如果当前结点不空,则将其入栈,再利用tempNode = tempNode.leftChild不断往下迭代左子树,具体来说就是不断地将当前结点的左子树作为新的当前结点;如果当前结点为空,则说明当前结点的根结点没有左子树,所以根据中序遍历“左 根 右”的顺序要求,此时就直接输出当前结点的根结点,也就是输出此时的栈顶元素(注意先出栈再打印);然后,将该出栈元素的右子树作为新的当前结点,继续判断。
/**
*********************
* In-order visit with stack.
*********************
*/
public void inOrderVisitWithStack() {
ObjectStack tempStack = new ObjectStack();
BinaryCharTree tempNode = this;
while(!tempStack.isEmpty() || tempNode != null) {
if(tempNode != null) {
tempStack.push(tempNode);
tempNode = tempNode.leftChild;
} else {
tempNode = (BinaryCharTree)tempStack.pop();
System.out.print("" + tempNode.value + " ");
tempNode = tempNode.rightChild;
} // Of if
} // Of while
} // Of inOrderVisitWithStack最后,我们用昨天创建的二叉树tempTree2来进行数据测试,如下:
System.out.println("\r\nIn-order visit with stack: ");
tempTree2.inOrderVisitWithStack();完整的程序代码:
package datastructure.tree;
import datastructure.*;
import java.util.Arrays;
/**
* Binary tree with char type elements.
*
*@auther Xin Lin 3101540094@qq.com.
*/
public class BinaryCharTree {
/**
* The value
*/
char value;
/**
* The left child
*/
BinaryCharTree leftChild;
/**
* The right child
*/
BinaryCharTree rightChild;
/**
*********************
* The first constructor.
*
* @param paraName The value.
*********************
*/
public BinaryCharTree(char paraName) {
value = paraName;
leftChild = null;
rightChild = null;
} // Of constructor
/**
*********************
* Manually construct a tree. Only for testing.
*********************
*/
public static BinaryCharTree manualConstructTree() {
// Step 1. Construct a tree with only one node.
BinaryCharTree resultTree = new BinaryCharTree('a');
// Step 2. Construct all Nodes. The first node is the root.
// BinaryCharTree tempTreeA = resultTree.root;
BinaryCharTree tempTreeB = new BinaryCharTree('b');
BinaryCharTree tempTreeC = new BinaryCharTree('c');
BinaryCharTree tempTreeD = new BinaryCharTree('d');
BinaryCharTree tempTreeE = new BinaryCharTree('e');
BinaryCharTree tempTreeF = new BinaryCharTree('f');
BinaryCharTree tempTreeG = new BinaryCharTree('g');
// Step 3. Link all Nodes.
resultTree.leftChild = tempTreeB;
resultTree.rightChild = tempTreeC;
tempTreeB.rightChild = tempTreeD;
tempTreeC.leftChild = tempTreeE;
tempTreeD.leftChild = tempTreeF;
tempTreeD.rightChild = tempTreeG;
return resultTree;
} // Of manualConstructTree
/**
*********************
* Pre-order visit.
*********************
*/
public void preOrderVisit() {
System.out.print("" + value + " ");
if(leftChild != null) {
leftChild.preOrderVisit();
} // Of if
if(rightChild != null) {
rightChild.preOrderVisit();
} // Of if
} // Of preOrderVisit
/**
*********************
* In-order visit.
*********************
*/
public void inOrderVisit() {
if(leftChild != null) {
leftChild.inOrderVisit();
} // Of if
System.out.print("" + value + " ");
if(rightChild != null) {
rightChild.inOrderVisit();
} // Of if
} // Of inOrderVisit
/**
*********************
* Post-order visit.
*********************
*/
public void postOrderVisit() {
if(leftChild != null) {
leftChild.postOrderVisit();
} // Of if
if(rightChild != null) {
rightChild.postOrderVisit();
} // Of if
System.out.print("" + value + " ");
} // Of postOrderVisit
/**
*********************
* Get the depth of the binary char tree.
*
* @return The depth.
*********************
*/
public int getDepth() {
if((leftChild == null) && (rightChild == null)) {
return 1;
} // Of if
// The depth of the left child.
int tempLeftDepth = 0;
if(leftChild != null) {
tempLeftDepth = leftChild.getDepth();
} // Of if
// The depth of the right child.
int tempRightDepth = 0;
if(rightChild != null) {
tempRightDepth = rightChild.getDepth();
} // Of if
if(tempLeftDepth >= tempRightDepth) {
return tempLeftDepth + 1;
} else {
return tempRightDepth + 1;
} // Of if
} // Of getDepth
/**
*********************
* Get the number of nodes of the binary char tree.
*
* @return The number of nodes.
*********************
*/
public int getNumNodes() {
if((leftChild == null) && (rightChild == null)) {
return 1;
} // Of if
// The number of nodes of the left child.
int tempLeftNodes = 0;
if(leftChild != null) {
tempLeftNodes = leftChild.getNumNodes();
} // Of if
// The number of nodes of the right child.
int tempRightNodes = 0;
if(rightChild != null) {
tempRightNodes = rightChild.getNumNodes();
} // Of if
// The total number of nodes.
return tempLeftNodes + tempRightNodes + 1;
} // Of getNumNodes
/**
* The values of nodes according to breadth first traversal.
*/
char[] valuesArray;
/**
* The indices in the complete binary tree.
*/
int[] indicesArray;
/**
********************
* Convert the tree to data arrays, including a char array and an int array.
* The results are stored in two member variables.
*
* @see #valuesArray
* @see #indicesArray
*********************
*/
public void toDataArrays() {
//Initialize arrays.
int tempLength = getNumNodes();
valuesArray = new char[tempLength];
indicesArray = new int[tempLength];
int i = 0;
//Traverse and convert at the same time.
CircleObjectQueue tempQueue = new CircleObjectQueue();
tempQueue.enqueue(this);
CircleIntQueue tempIntQueue = new CircleIntQueue();
tempIntQueue.enqueue(0);
BinaryCharTree tempTree = (BinaryCharTree) tempQueue.dequeue();
int tempIndex = tempIntQueue.dequeue();
while (tempTree != null) {
valuesArray[i] = tempTree.value;
indicesArray[i] = tempIndex;
i++;
if (tempTree.leftChild != null) {
tempQueue.enqueue(tempTree.leftChild);
tempIntQueue.enqueue(tempIndex * 2 + 1);
} // Of if
if (tempTree.rightChild != null) {
tempQueue.enqueue(tempTree.rightChild);
tempIntQueue.enqueue(tempIndex * 2 + 2);
} // Of i
tempTree = (BinaryCharTree) tempQueue.dequeue();
tempIndex = tempIntQueue.dequeue();
} // Of while
} // Of toDataArrays
/**
********************
* Convert the tree to data arrays, including a char array and an int array.
* The results are stored in two member variables.
*
* @see #valuesArray
* @see #indicesArray
*********************
*/
public void toDataArraysObjectQueue() {
//Initialize arrays.
int tempLength = getNumNodes();
valuesArray = new char[tempLength];
indicesArray = new int[tempLength];
int i = 0;
//Traverse and convert at the same time.
CircleObjectQueue tempQueue = new CircleObjectQueue();
tempQueue.enqueue(this);
CircleObjectQueue tempIntQueue = new CircleObjectQueue();
Integer tempIndexInteger = Integer.valueOf(0);
tempIntQueue.enqueue(tempIndexInteger);
BinaryCharTree tempTree = (BinaryCharTree) tempQueue.dequeue();
int tempIndex = ((Integer)tempIntQueue.dequeue()).intValue();
System.out.println("tempIndex = " + tempIndex);
while (tempTree != null) {
valuesArray[i] = tempTree.value;
indicesArray[i] = tempIndex;
i++;
if (tempTree.leftChild != null) {
tempQueue.enqueue(tempTree.leftChild);
tempIntQueue.enqueue(Integer.valueOf(tempIndex * 2 + 1));
} // Of if
if (tempTree.leftChild != null) {
tempQueue.enqueue(tempTree.leftChild);
tempIntQueue.enqueue(Integer.valueOf(tempIndex * 2 + 2));
} // Of if
tempTree = (BinaryCharTree) tempQueue.dequeue();
if (tempTree == null) {
break;
} // Of if
tempIndex = ((Integer)tempIntQueue.dequeue()).intValue();
} // Of while
} // Of toDataArraysObjectQueue
/**
*********************
* The second constructor. The parameters must be correct since no validity
* check is undertaken.
*
* @param paraDataArray The array for data.
* @param paraIndicesArray The array for indices.
*********************
*/
public BinaryCharTree(char[] paraDataArray, int[] paraIndicesArray) {
// Step 1. Use a sequential list to store all nodes.
int tempNumNodes = paraDataArray.length;
BinaryCharTree[] tempAllNodes = new BinaryCharTree[tempNumNodes];
for(int i = 0; i < tempNumNodes; i++) {
tempAllNodes[i] = new BinaryCharTree(paraDataArray[i]);
} // Of for i
// Step 2. Link all nodes.
for(int i = 1; i < tempNumNodes; i++) {
for(int j = 0; j < i; j++) {
System.out.println("Indices " + paraIndicesArray[j] + " vs. " + paraIndicesArray[i]);
if(paraIndicesArray[i] == paraIndicesArray[j] * 2 + 1) {
tempAllNodes[j].leftChild = tempAllNodes[i];
System.out.println("Linking " + j + " with " + i);
break;
} // Of if
if(paraIndicesArray[i] == paraIndicesArray[j] * 2 + 2) {
tempAllNodes[j].rightChild = tempAllNodes[i];
System.out.println("Linking " + j + " with " + i);
break;
} // Of if
} // Of for j
} // Of for i
// Step 3. The root is the first node.
value = tempAllNodes[0].value;
leftChild = tempAllNodes[0].leftChild;
rightChild = tempAllNodes[0].rightChild;
} // Of the the second constructor
/**
*********************
* In-order visit with stack.
*********************
*/
public void inOrderVisitWithStack() {
ObjectStack tempStack = new ObjectStack();
BinaryCharTree tempNode = this;
while(!tempStack.isEmpty() || tempNode != null) {
if(tempNode != null) {
tempStack.push(tempNode);
tempNode = tempNode.leftChild;
} else {
tempNode = (BinaryCharTree)tempStack.pop();
System.out.print("" + tempNode.value + " ");
tempNode = tempNode.rightChild;
} // Of if
} // Of while
} // Of inOrderVisitWithStack
/**
*********************
* The entrance of the program.
*
* @param args Not used now.
*********************
*/
public static void main(String args[]) {
BinaryCharTree tempTree = manualConstructTree();
System.out.println("\r\nPreorder visit:");
tempTree.preOrderVisit();
System.out.println("\r\nIn-order visit:");
tempTree.inOrderVisit();
System.out.println("\r\nPost-order visit:");
tempTree.postOrderVisit();
System.out.println("\r\n\r\nThe depth is: " + tempTree.getDepth());
System.out.println("The number of nodes is: " + tempTree.getNumNodes());
tempTree.toDataArrays();
System.out.println("The values are: " + Arrays.toString(tempTree.valuesArray));
System.out.println("The indices are: " + Arrays.toString(tempTree.indicesArray));
tempTree.toDataArraysObjectQueue();
System.out.println("Only object queue.");
System.out.println("The values are: " + Arrays.toString(tempTree.valuesArray));
System.out.println("The indices are: " + Arrays.toString(tempTree.indicesArray));
char[] tempCharArray = {'A', 'B', 'C', 'D', 'E', 'F'};
int[] tempIndices = {0, 1, 2, 4, 5, 12};
BinaryCharTree tempTree2 = new BinaryCharTree(tempCharArray, tempIndices);
System.out.println("\r\nPreorder visit:");
tempTree2.preOrderVisit();
System.out.println("\r\nIn-order visit:");
tempTree2.inOrderVisit();
System.out.println("\r\nPost-order visit:");
tempTree2.postOrderVisit();
System.out.println("\r\nIn-order visit with stack: ");
tempTree2.inOrderVisitWithStack();
}// Of main
} // Of class BinaryCharTree运行结果:
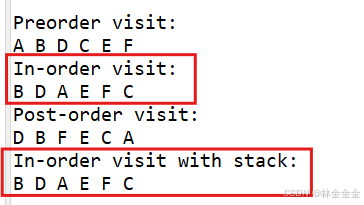
可以发现,对于同一棵二叉树tempTree2,我们今天用栈实现的中序遍历和我们昨天用递归实现的中序遍历,其结果是一模一样的,说明代码可行。
总结
今天,我们主要学习的就是如何利用栈来实现二叉树的中序遍历,其本质上就是递归思维和迭代思维的相互转化。单看今天的代码量的话,其实挺少的,但是如果想要说清楚理透彻这两种思维的转化过程,似乎就比较困难了,本文也只是作者个人一些浅薄的理解,如有误,欢迎批评指正。
通过今天的学习,我们可以发现果然还是递归用起来简单,不过我们还是需要像二叉树遍历这种较为复杂的迭代操作,这对于锻炼一个程序员的迭代思维还是非常好的。