分层神经网络作为深度学习的核心架构，已经彻底改变了我们处理复杂问题的方式。本文将带我们走进神经网络的基础知识，揭开GPT这些强大模型的神秘面纱。希望通过本文的介绍，我们不仅能够理解神经网络的基本构成，还能洞察到它们是如何通过一系列精心设计的层次结构来学习和模拟数据中的复杂模式。

神经网络由什么构成？

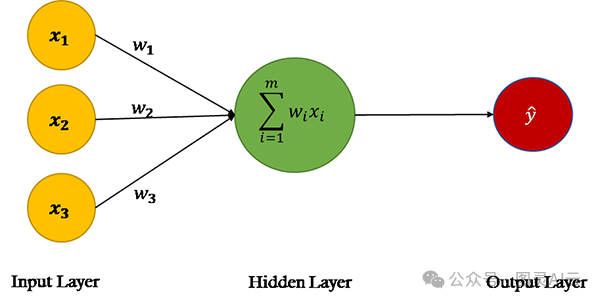
所有神经网络都由神经元网络组成，就像它们所模拟的大脑一样，但神经元是什么？

一个神经元由其输入、权重、偏差、激活函数和单一输出组成。它最初旨在复制生物神经元。

输入和权重之间存在一一对应的比例，当它们结合在一起时，会得到一系列加权输入，这些输入会被相加。在这个总和上加上一个偏差。

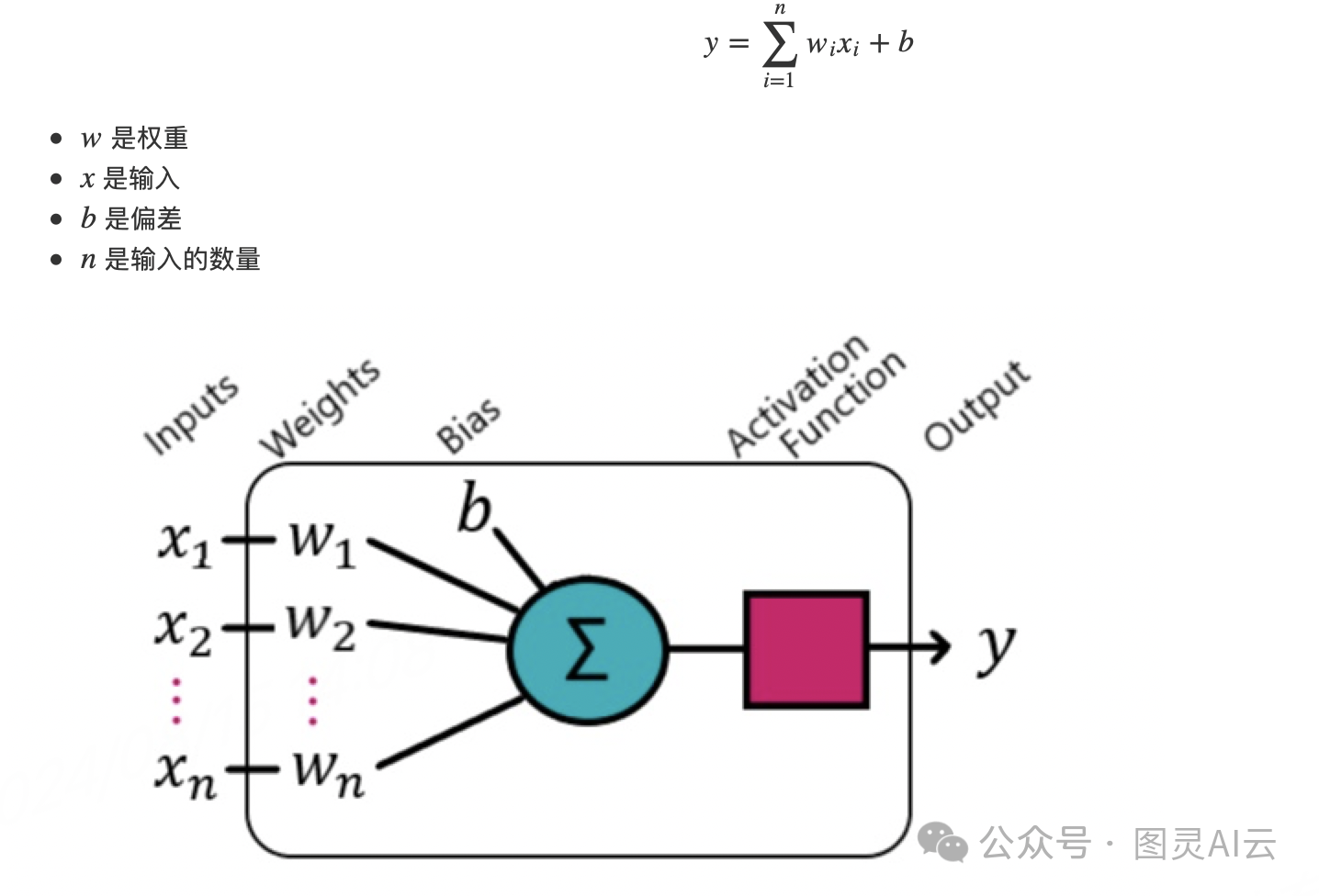
激活函数为什么重要？

具有单个输入的神经元是一个线性函数 ( y = ax + b )，因此只能形成简单的决策边界。即使增加神经网络中输入和神经元的数量，结果仍然是线性函数。这是因为多个线性函数结合在一起总是得到线性函数。

为了解决这个问题，并允许网络找到复杂的决策边界，我们需要使用激活函数，它们增加了非线性。

在下面的图表中，你可以看到这一点的例子，虚线代表具有单个加权输入的神经元，实线红线是三个的总和。看看在第一张图中红线仍然是一个线性函数。从数学上讲，这是因为 ( (4x + 2) + (-3x - 4) + (-2x + 1) ) 简化为 ( (-x - 1) )。

 

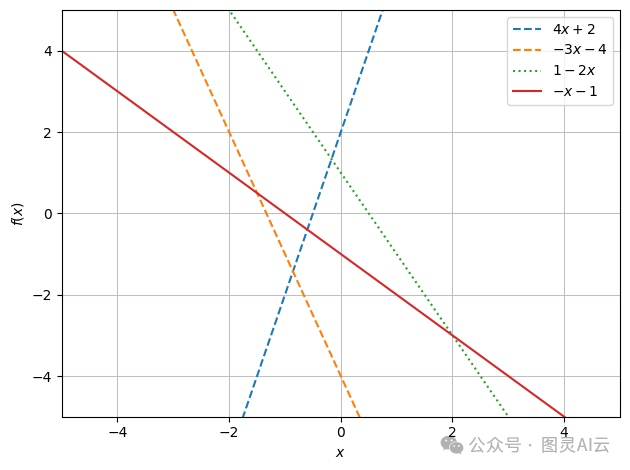
当将相同的神经元通过激活函数，在这个例子中是逻辑函数，非线性被添加到系统中。

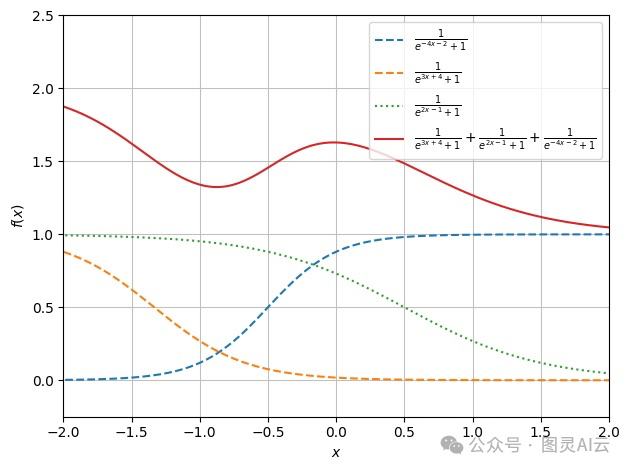
以下是一些更知名的激活函数：

 

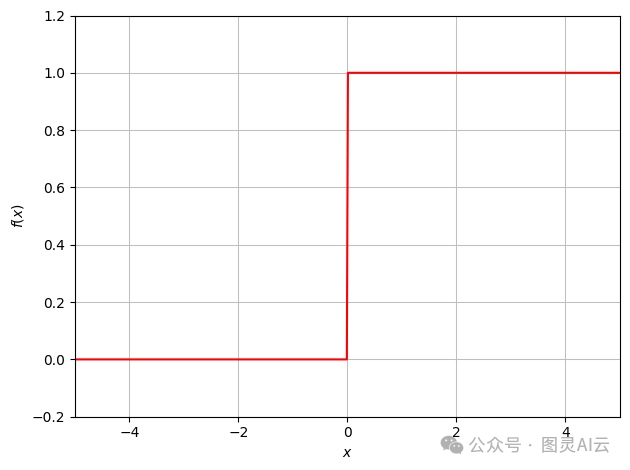
由于历史原因，这是最初的激活函数，20世纪50年代最初的感知机中使用了这个函数。这个函数将求和函数的输出转换为二进制值。

由于函数中阶梯的性质，权重和偏差的变化在输出越过阶梯边界之前不会有任何影响，一旦越过，它就会翻转二进制值。

步进函数

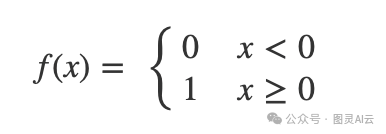
由于函数中步进的特性，权重和偏差的变化在输出越过步进边界之前没有影响，在这一点上它会翻转二进制值。

逻辑函数，也称Sigmoid函数

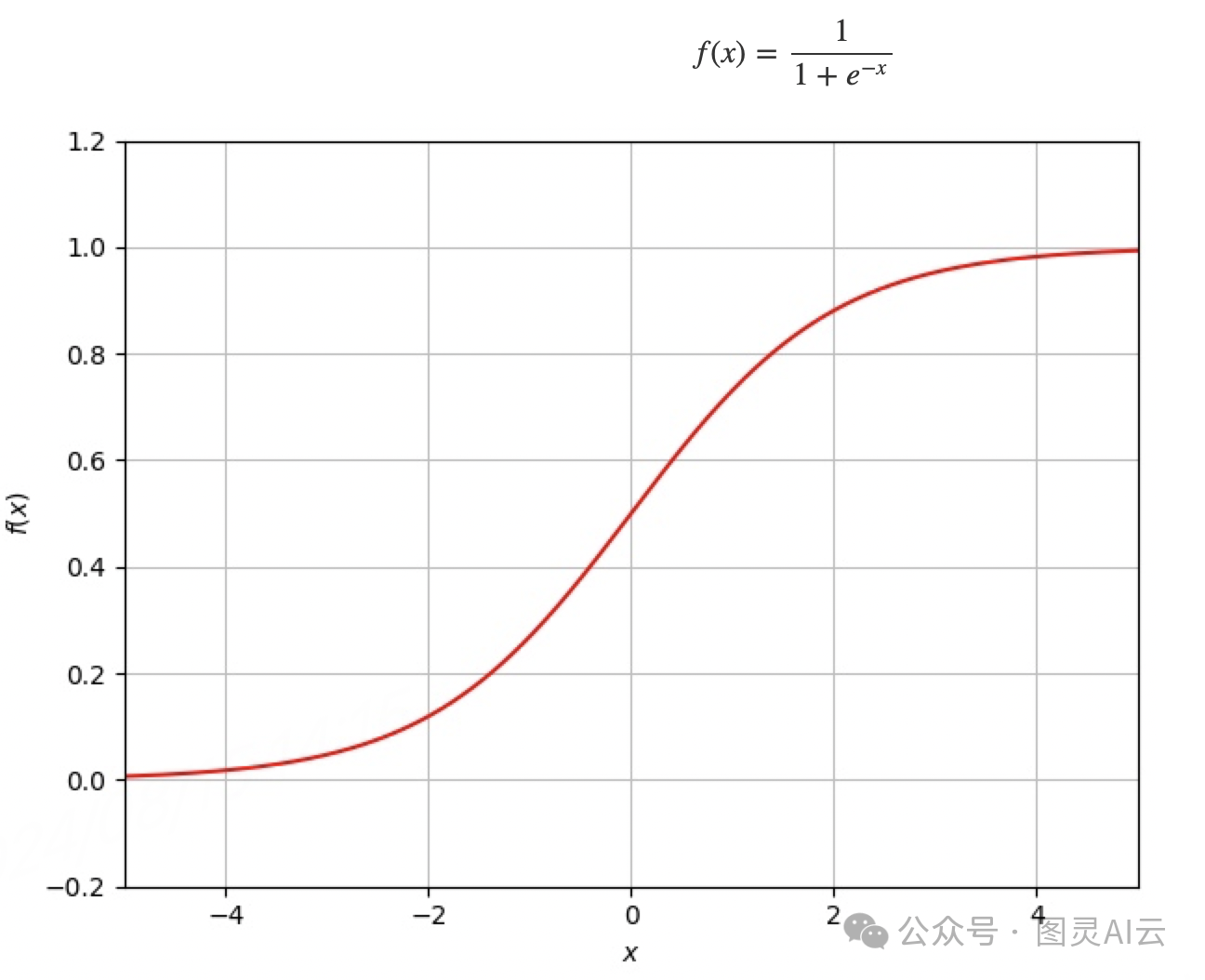
逻辑函数，即Sigmoid函数的一个变体，最初取代了阶梯函数。与阶梯函数一样，它将一个神经元的输出限制在0和1之间，但不会在零点附近出现同样的问题。这使得训练过程更加容易，因为除了在极端情况下，权重和偏差的变化始终会产生影响。

修正线性单元（ReLU）

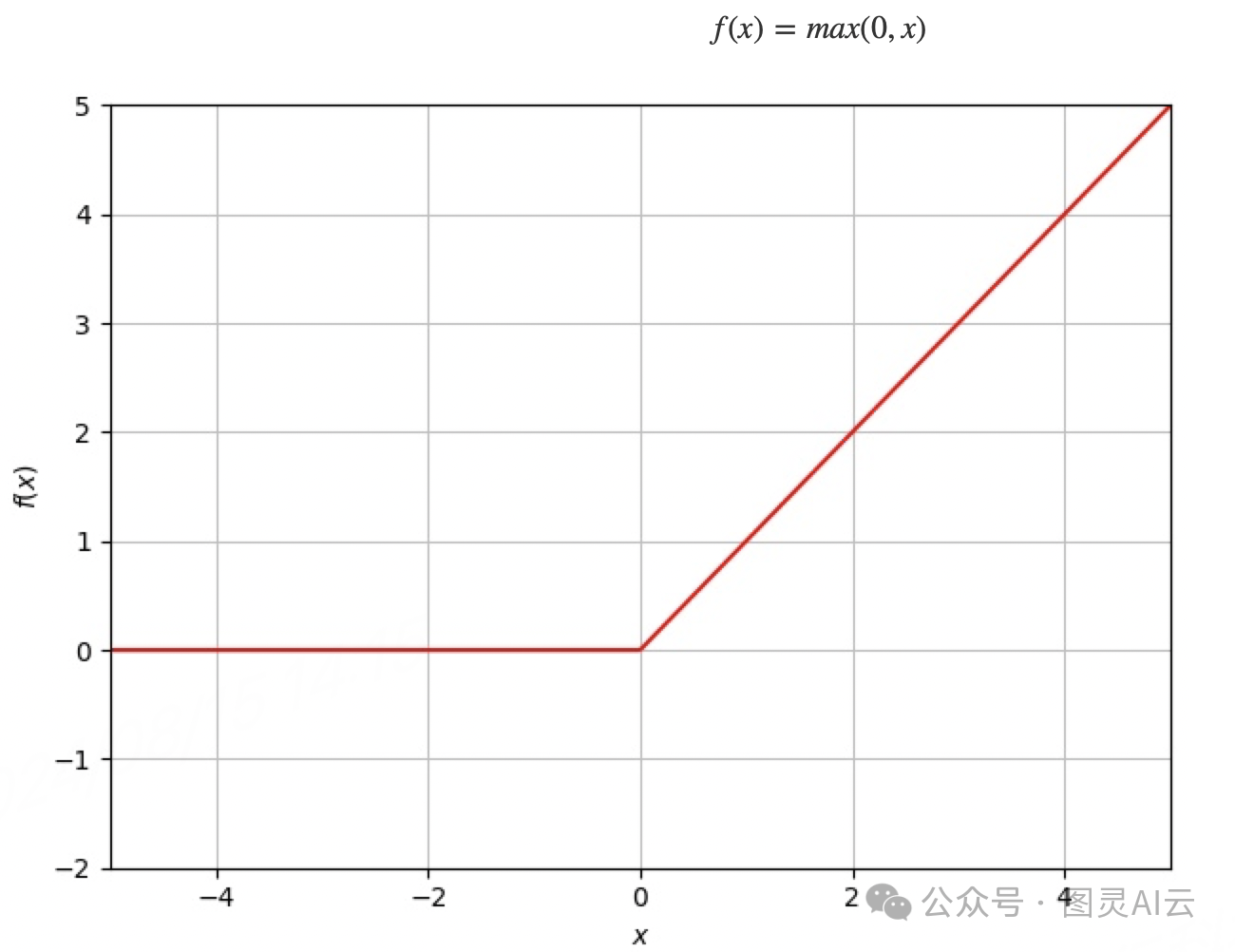
修正线性单元（Rectified Linear Unit，简称ReLU）已经成为最受欢迎的激活函数，并且在大多数情况下，它是深度神经网络使用的默认激活函数。ReLU将输入的值与0进行比较，取两者中的较大值，这实际上会立即将任何负的输入值置为0。这种特性使得ReLU在处理正数时保持线性，而在处理负数时则输出0，从而加快了神经网络的训练速度，并有助于解决梯度消失问题。

SoftMax

SoftMax激活函数用于分类神经网络的最终输出层。它将输出值的向量转换为输出类别的概率分布。每个输出神经元将代表输入属于相应类别的概率。

神经网络的架构

在神经网络中，神经元可以以多种方式排列。对于基本神经网络，神经元被安排成几个不同的层次。

有三个类别：

1. 输入层

2. 隐藏层

3. 输出层

1. 输入层

输入层纯粹是输入数据的值，不进行计算。对于图像分类神经网络，每个输入值都有一个神经元，对于灰度图像，每个像素都有一个神经元。

2. 隐藏层

隐藏层是神经网络的主力，它们负责识别特征或将输入转换为输出层可以使用的东西。

如果有单个隐藏层，那么神经网络是一个浅层神经网络。如果有两个或更多隐藏层，那么它是一个深度学习神经网络。神经网络越深，它可以学习的模式就越复杂，但这需要更多的计算能力来训练。

每个隐藏层中可以有任意数量的神经元，神经元数量的增加可以提高神经网络在输入中识别信息的能力。但神经元数量的增加可能导致对训练数据的过拟合。

3. 输出层

输出层给出了神经网络的输出。对于图像分类，将有一个神经元对应于要分类的每个类别，例如在手写数字识别中，将有10个神经元，每个数字一个。

层如何连接

对于基本的分层神经网络，每个神经元将前一层中每个神经元的输出作为其输入。第一个隐藏层直接接受神经网络的输入。

 

已经证明，具有两层并使用非线性激活函数的神经网络可以是一个通用函数逼近器，可以找到任何数学函数。

确定权重和偏差（参数）

那么每个神经元的权重和偏差是如何设置的？

权重和偏差，参数，可以手动更新，直到神经网络的输出正确。然而，神经网络可能包含数百万/数十亿个参数，因此需要自动化过程。

为了能够自动化这个过程，需要一种评估神经网络准确性的方法。为此，可以使用损失函数来给出一个值，显示当前神经网络离正确评估有多远。

损失函数

寻找神经网络误差的常用算法是均方误差函数。这会找到一个正值，显示网络离期望值有多远。

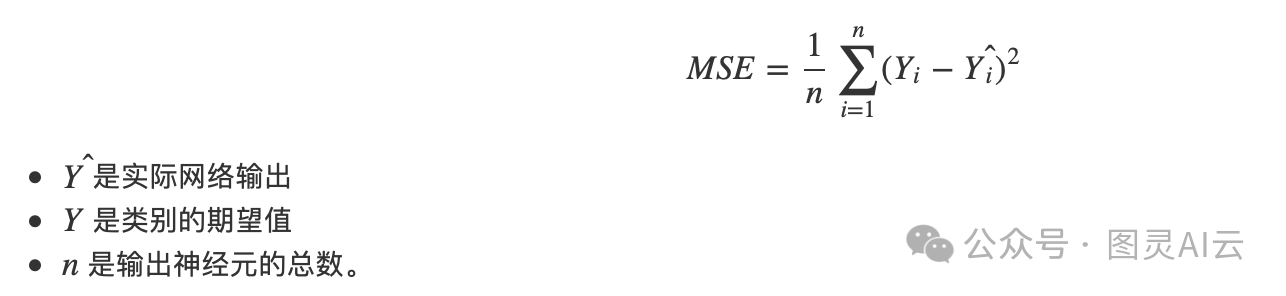
损失函数可以进行经验分析，看看参数的变化是否改善或恶化了神经网络的输出。目标是尽可能地改变参数以最小化损失。

梯度下降

假设一个具有单个输入的神经网络，有一个权重。如果我们绘制权重与损失的图表，可能会有像下面的图表。

 

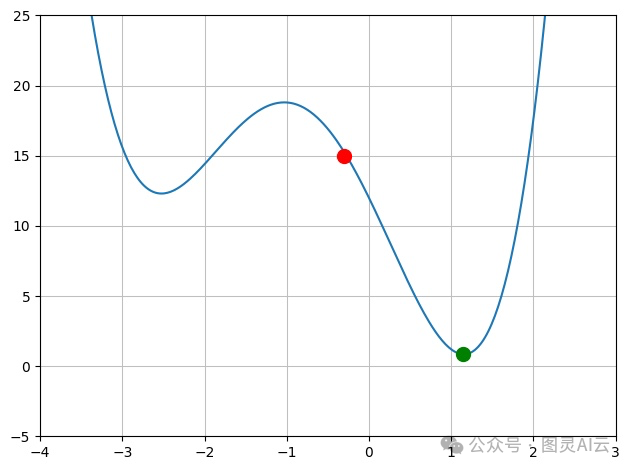
假设红色标记是基于当前权重的当前误差值，绿色点是最小误差。目标是计算给我们最小值的权重值。

为了计算新的权重值，取权重误差的导数并从当前权重中减去该值。实际上，找到了沿着图表斜率向下走向局部或全局最小值的新值。

学习率用于控制对权重的更改量，如果权重变化的大小太大，则可能会跳过损失最小值，或者它可能永远不会在最小值的“山谷”中定居，并不断地从一边跳到另一边。如果太小，那么到达局部最小值将需要更长的时间。

反向传播

为了计算每个权重的调整，然后需要计算相对于每个权重变化的误差变化的梯度。对于最后一层来说很简单，但对于前几层则不是那么简单。

可以使用一种称为反向传播的数学概念来确定这一点，从最后一层开始，逐层向前一层计算导数。

反向传播中使用了称为链式法则的微积分概念，以计算相对于每层的输入、权重和偏差的误差函数的梯度。