0. 前言
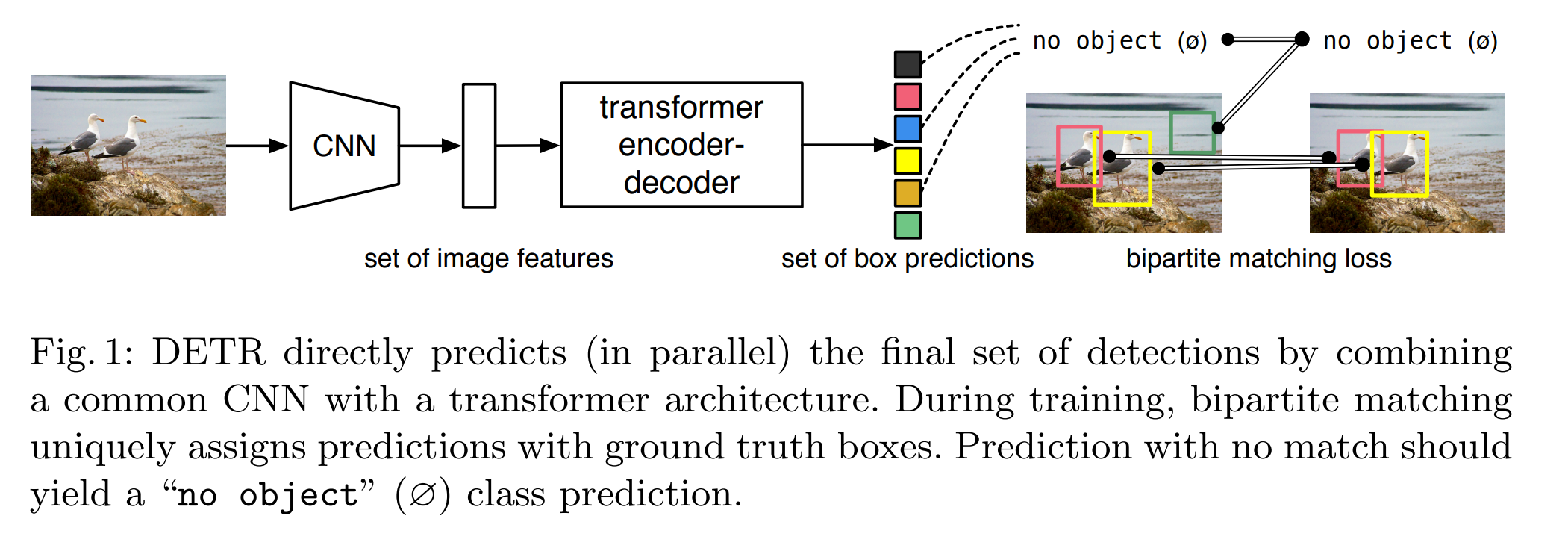
DETR是首个将Transformer应用到2D目标检测任务中的算法,由Facebook于2020年在论文《End-to-End Object Detection with Transformers》中提出。与传统目标检测算法不同的是,DETR将目标检测任务视为一个直接的集合预测问题,采用基于集合的全局损失通过二分匹配实现一对一的预测输出,不需要非极大值抑制(NMS)和手工设计Anchor这些操作,基于Transformer的编码器-解码器架构实现了端到端的目标检测,整个实现流程非常简单明了。
如果对Transformer还不是很了解的话可以看我之前的这篇文章:
Transformer模型结构解析与Python代码实现
1. 实现细节
1.1 网络结构
DETR的网络结构非常简单,主要包括三个部分:一个用于提取图像特征的CNN骨干网络,一个基于编码器-解码器的Transformer结构,一个用于实现最终检测预测的前馈网络(FFN)。

骨干网络
对于一张输入图片 x i m g ∈ R 3 × H 0 × W 0 x_{img} \in \mathbb{R} ^{3 \times H_{0} \times W_{0}} ximg∈R3×H0×W0,基于传统CNN的骨干网络会输出多个通道的低分辨率特征图 f ∈ R C × H × W f \in \mathbb{R} ^{C \times H \times W} f∈RC×H×W,其中 C = 2048 C=2048 C=2048, H = H 0 / 32 H=H_{0}/32 H=H0/32, W = W 0 / 32 W=W_{0}/32 W=W0/32。
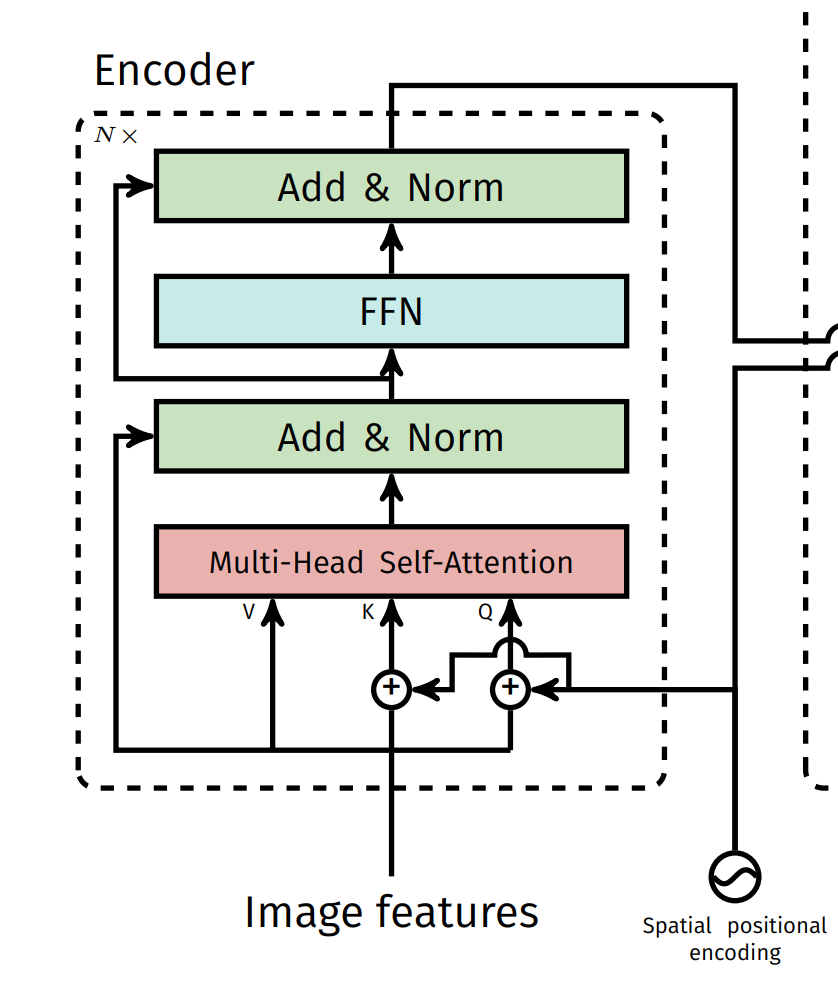
Transformer编码器
首先通过
1
×
1
1 \times 1
1×1的卷积层将特征图
f
f
f的通道数由
C
C
C减少到
d
d
d,得到新的特征图
z
0
∈
R
d
×
H
×
W
z_{0} \in \mathbb{R} ^{d \times H \times W}
z0∈Rd×H×W,由于Transformer需要输入一个序列,因此还需要特征图
z
0
z_{0}
z0的维度变换为
d
×
H
W
d \times HW
d×HW。每个编码器层都由一个多头自注意模块和一个前馈网络组成,每个注意力层的输入中都会添加位置编码。
Transformer解码器
解码器与标准的Transformer解码器相同,由自注意力和交叉注意力层组成。不同的是,DETR的解码器在每个解码器层并行地解码N个对象。由于解码器也是置换不变的,因此N个输入嵌入必须不同才能产生不同的输出结果,因此在每个注意力层的输入中也需要添加位置编码。N个输入嵌入是可学习的位置编码参数,作者称之为目标查询(object queries)。目标查询经过解码器被转换为输出嵌入,然后送入前馈网络中独立解码为目标框的坐标和类别标签,产生N个最终的预测结果。
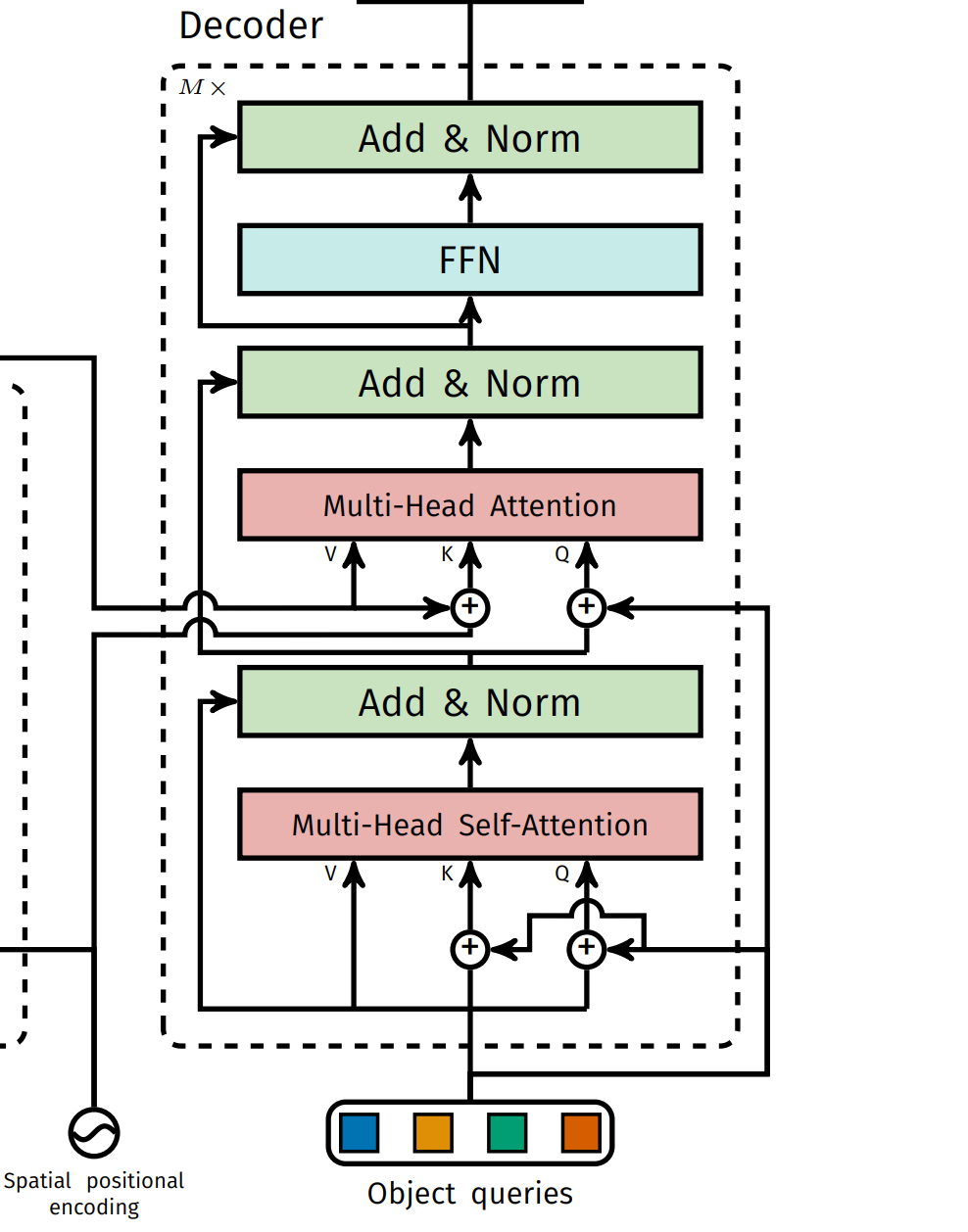
前馈网络
前馈网络由带ReLU激活函数的3层感知机以及1个线性映射层组成,输出的预测结果为归一化的目标中心点坐标,检测框相对于输入图像的宽高以及所属类别的标签。模型总共预测N个目标的信息,其中N是一个远大于通常图像中目标数量的常数(比如100)。此外,作者还使用一个额外的特殊类别$\phi $表示空目标,类似于传统目标检测任务中的背景类别。
1.2 损失函数
目标检测集合预测损失
假设N个预测结果为
y
^
=
{
y
^
i
}
i
=
1
N
\hat{y} =\left \{ \hat{y}_{i} \right \}_{i=1}^{N}
y^={y^i}i=1N,对应的一组目标的真值为
y
y
y,其中
y
y
y用空目标$\phi $进行补齐到N的大小。为了找到真值与预测结果的最优匹配,我们的目标是求匹配代价最小的一组匹配对:
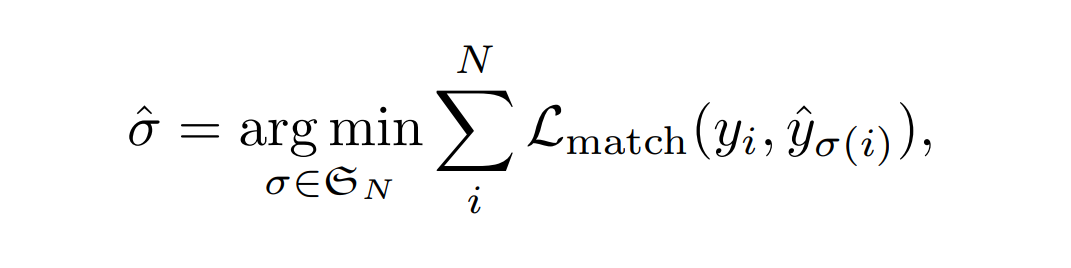
其中, L m a t c h ( y i , y ^ δ ( i ) ) \mathcal{L}_{match}(y_{i},\hat{y}_{\delta (i)}) Lmatch(yi,y^δ(i))表示真值 y i y_{i} yi与预测结果 y ^ δ ( i ) \hat{y}_{\delta (i)} y^δ(i)之间的匹配代价,最优分配可以通过匈牙利算法高效地求得。
匹配代价同时考虑了类别预测结果以及预测的框和真实框的相似度。每个真值可以定义为
y i = ( c i , b i ) y_{i}=(c_{i},b_{i}) yi=(ci,bi)
其中 c i c_{i} ci表示类别标签(可能为空目标$\phi ), ), ),b_{i} \in [0,1]^{4}$是一个包含真实框的中心点坐标和宽高(相对于输入图像尺寸)的向量。
对于一个序号为 δ ( i ) \delta (i) δ(i)的预测结果 y ^ δ ( i ) \hat{y}_{\delta (i)} y^δ(i),定义其类别为 c i c_{i} ci的概率为 p ^ δ ( i ) ( c i ) \hat{p}_{\delta (i)}(c_{i}) p^δ(i)(ci),预测框为 b ^ δ ( i ) \hat{b}_{\delta (i)} b^δ(i)。那么真值 y i y_{i} yi与预测结果 y ^ δ ( i ) \hat{y}_{\delta (i)} y^δ(i)之间的匹配代价 L m a t c h ( y i , y ^ δ ( i ) ) \mathcal{L}_{match}(y_{i},\hat{y}_{\delta (i)}) Lmatch(yi,y^δ(i))可以表示为
L m a t c h ( y i , y ^ δ ( i ) = − 1 { c i ≠ ϕ } p ^ δ ( i ) ( c i ) + 1 { c i ≠ ϕ } L b o x ( b i , b ^ δ ( i ) ) \mathcal{L}_{match}(y_{i},\hat{y}_{\delta (i)}=\mathbb{-1}_{\left \{ c_{i}\ne \phi \right \}} \hat{p}_{\delta (i)}(c_{i}) + \mathbb{1}_{\left \{ c_{i}\ne \phi \right \}} \mathcal{L}_{box} (b_{i},\hat{b}_{\delta (i)}) Lmatch(yi,y^δ(i)=−1{ci=ϕ}p^δ(i)(ci)+1{ci=ϕ}Lbox(bi,b^δ(i))
接下来是计算所有匹配对的匈牙利匹配损失:
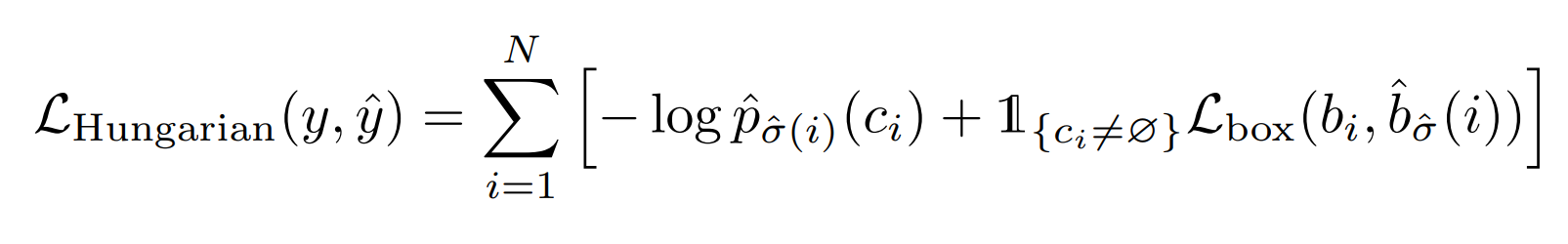
出于类别平衡的考虑,当 c i = ϕ c_{i}=\phi ci=ϕ时,作者会降低对数概率项的权重。
Bounding box损失
Bounding box损失
L
b
o
x
(
⋅
)
\mathcal{L}_{box}(\cdot)
Lbox(⋅)是
l
1
\mathcal{l_{1}}
l1损失和GIoU损失的线性组合:
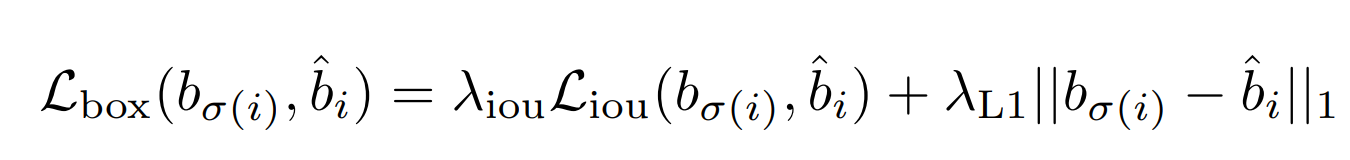
其中
λ
i
o
u
,
λ
L
1
∈
R
\lambda _{iou},\lambda _{L1} \in \mathbb{R}
λiou,λL1∈R是超参数,
L
i
o
u
(
⋅
)
\mathcal{L}_{iou}(\cdot)
Liou(⋅)是GIoU损失
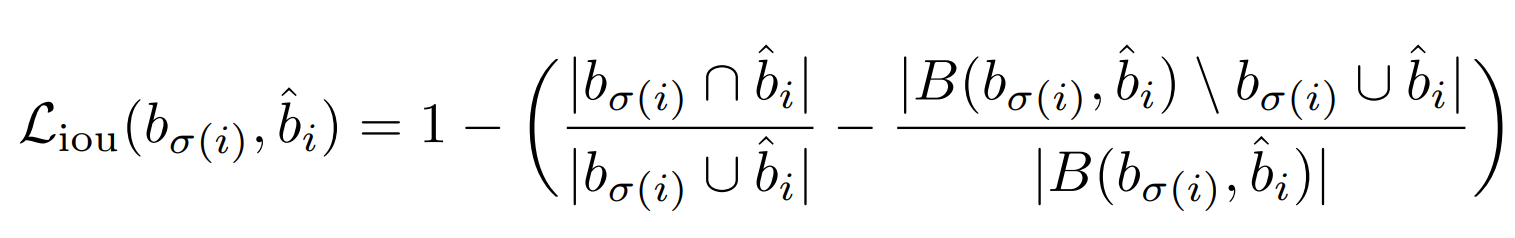
其中 ∣ ⋅ ∣ \left | \cdot \right | ∣⋅∣表示求面积。
2. 扩展
DETR具有很好的扩展性,作者在Transformer解码器输出的顶部添加了一个掩码头用于预测每个预测框的二进制掩码,将其扩展到全景分割任务中去。这个掩码头将每个对象Transformer解码器的输出作为输入,并在编码器的输出上计算此嵌入的多头(有M个头)注意力分数,为每个对象生成M个小分辨率的注意力热图。为了做出最终预测并提高分辨率,作者使用了类似FPN的架构。
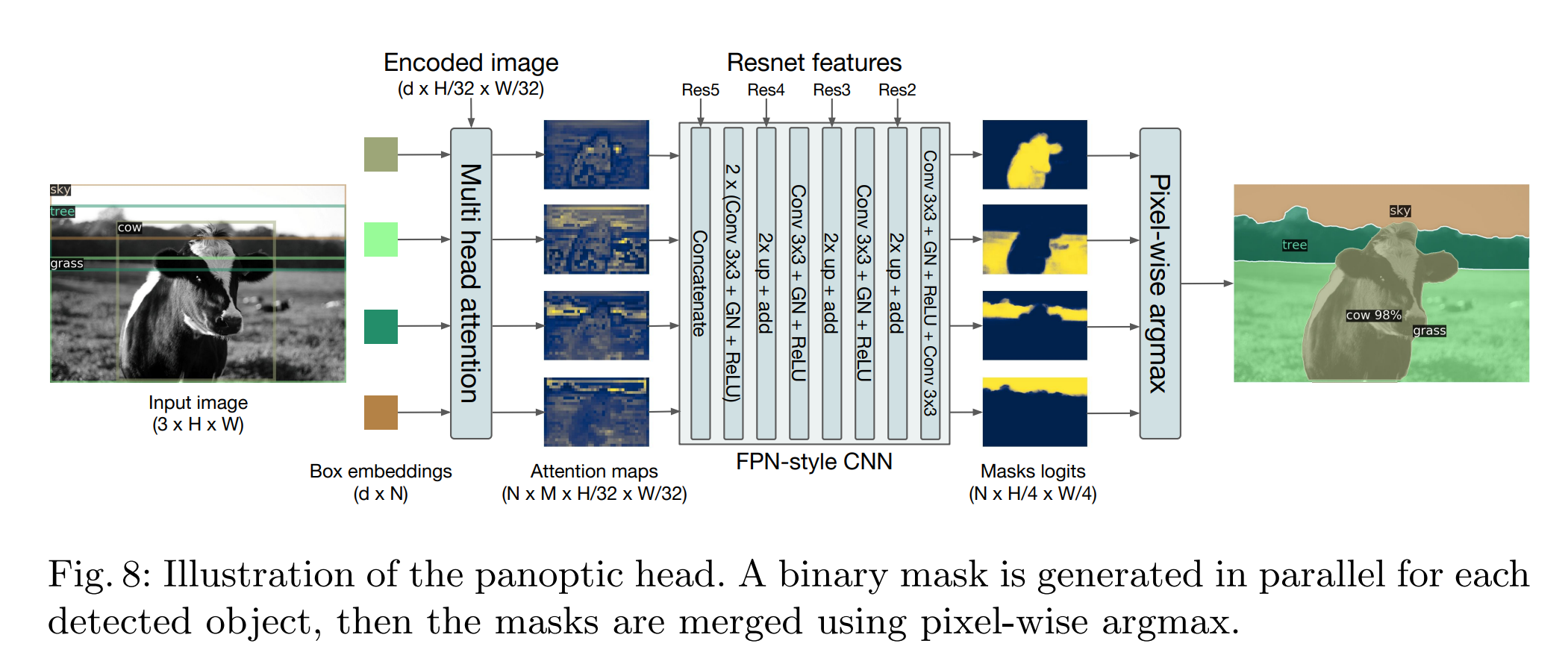
每个掩码都采用DICE/F-1 loss和Focal loss独立地进行监督训练,DICE损失的定义如下:
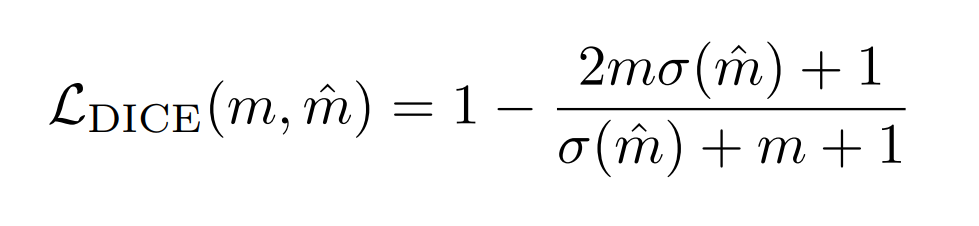
其中$\delta $表示sigmoid函数,loss值会根据目标数量进行归一化。
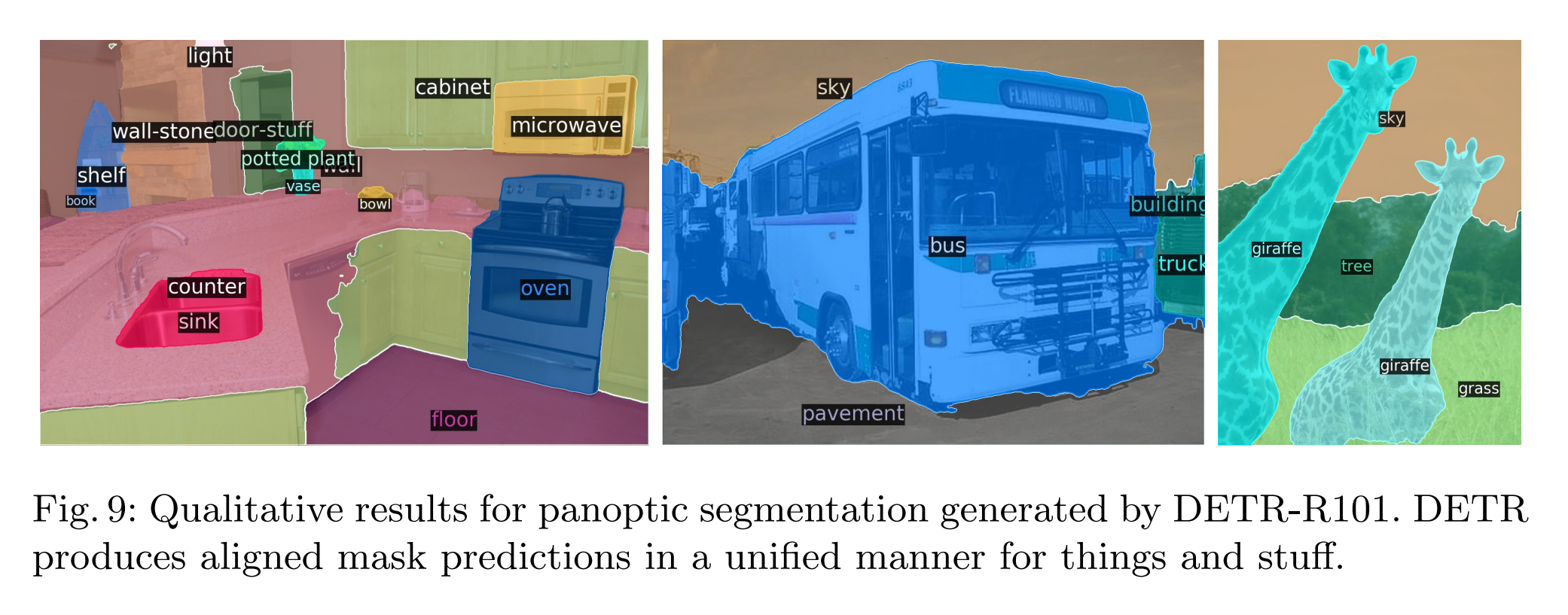
分割效果:
3. 参考资料
- 《
End-to-End Object Detection with Transformers》