图像二值化（Image Binarization）是指将像素点的灰度值设为0或255，使图像呈现明显的黑白效果。二值化一方面减少了数据维度，另一方面通过排除原图中噪声带来的干扰，可以凸显有效区域的轮廓结构。OCR效果很大程度上取决于该步骤，高质量的二值图像可以显著提升识别的准确率。目前，二值化的方法主要分为全局阈值方法（Global Binarization）、局部阈值方法（Local Binarization）、基于深度学习的方法和其他方法。

固定阈值方法

该方法对输入图像中的所有像素点统一使用同一个固定阈值。其算法如下：
$$g(x,y)=\{\begin{array}{ll}255,& 若f(x,y)\ge T\\ 0,& 否则\end{array}$$

• $T$为全局阈值

不同的阈值$T$会产生不同的二值化效果。对于不同的输入图像，最佳的阈值$T$也不一样，这也是固定阈值方法的主要缺陷。
于是，解决这一缺陷的相应算法也随之而出现；下面的几种方法均采用了根据输入图像计算最佳阈值的思想。

Otsu算法

Ostu算法又称最大类间方差法，由日本学者Nobuyuki Ostu于1979年提出，是一种在自适应的阈值确定方法。
Ostu算法将输入图像分为$L$个灰度级，$n_i$表示灰度级为$i$的像素个数，则像素总数$N=n_1+n_2+\cdots +n_L$。为了简化讨论，这里使用归一化的灰度直方图，并将其视为输入图像的概率分布：
$$p_i=n_i/N,p_i>0,\sum _{i=1}^L{p}_i=1$$
现假设在第$k$个灰度级设置阈值，将图像分为$C_0$和$C_1$（背景和目标物体），$C_0$表示灰度级为$[1,\cdots ,k]$的像素点，$C_1$表示灰度级为$[k+1,\cdots ,L]$的像素点，那么两类出现的概率以及类内灰度级的均值分别为：
$$\begin{gathered} {\omega }_0=Pr(C_0)=\sum _{i=1}^k{p}_i=\omega (k) \\ {\omega }_1=Pr(C_1)=\sum _{i=k+1}^L{p}_i=1-\omega (k) \\ {\mu }_0=\sum _{i=1}^{k}iPr(i|C_0)=\sum _{i=1}^{k}i{p}_i/{\omega }_0=\mu (k)/\omega (k) \\ {\mu }_1=\sum _{i=k+1}^{L}iPr(i|C_1)=\sum _{i=k+1}^{k}i{p}_i/{\omega }_1=\frac{{\mu }_T-\mu (k)}{1-\omega (k)} \end{gathered}$$

• $\omega (k)$和$\mu (k)$分别为灰度级从1到$k$的累计出现概率和平均灰度级;
• ${\mu }_T$为整张图像的平均灰度级。

容易证得，对于任意$k$值均有：
$${\omega }_0{\mu }_0+{\omega }_1{\mu }_1={\mu }_T,{\omega }_0+{\omega }_1=1$$
这两类得类内方差也可以算得：
$$\begin{gathered} {\sigma }_0^2=\sum _{i=1}^k(i-{\mu }_0{)}^{2}Pr(i|C_0)=\sum _{i=1}^k(i-{\mu }_0{)}^2{p}_i/{\omega }_0 \\ {\sigma }_1^2=\sum _{i=k+1}^L(i-{\mu }_1{)}^{2}Pr(i|C_0)=\sum _{i=k+1}^L(i-{\mu }_1{)}^2{p}_i/{\omega }_1 \end{gathered}$$
为了评价阈值$k$的好坏，需要引入判别式：
$$\lambda ={\sigma }_B^2/{\sigma }_W^2,\kappa ={\sigma }_T^2/{\sigma }_W^2,\eta ={\sigma }_B^2/{\sigma }_T^2(1)$$

其中

• ${\sigma }_W^2={\omega }_0{\sigma }_0^2+{\omega }_1{\sigma }_1^2$，即类内方差
• ${\sigma }_B^2={\omega }_0({\mu }_0-{\mu }_T{)}^2+\omega ({\mu }_1-{\mu }_T{)}^2={\omega }_0{\omega }_1({\mu }_1-{\mu }_0{)}^2$，即类间方差
• ${\sigma }_T^2={\sum }_{i=1}^L(i-{\mu }_T{)}^2{p}_i$，即灰度级的总方差

由于${\sigma }_W^2+{\sigma }_B^2={\sigma }_T^2$始终成立，而对同一张图片来说${\sigma }_T^2$是确定的，所以${\sigma }_W^2$和${\sigma }_B^2$，一个越大，另一个就会越小。这样的话，(1)式中的三个目标值$\lambda ,\kappa ,\eta$就总是同向运动的。
但是从计算简单程度上来说，因为${\sigma }_T^2$与$k$无关，且${\sigma }_B^2$只涉及均值的运算。因此，$\eta$是判别$k$取值好坏的最简单的衡量标准：
$$\eta ={\sigma }_B^2(k)/{\sigma }_T^2$$
因此，最佳的$k$值选择（$k^{\ast }$）满足：
$${\sigma }_B^2(k^{\ast })=\underset{1\le k\le L}{\max }{\sigma }_B^2(k)$$

在OpenCV中的实现

固定阈值

固定阈值可以在OpenCV中用adptiveThreshold()函数来实现，其函数原型如下：

void cv::adptiveThreshold(	InputArray	src,
							OutputArray	dst,
							double		maxValue,
							int			adaptiveMethod,
							int			thresholdType,
							int			blockSize,
							double		C)

将其中的第5个参数thresholdType指定为THRESH_BINARY就是固定阈值方法。

Otsu算法

Otsu算法可以在OpenCV中用threshold()函数来实现，其函数原型如下：

double cv::threshold(	InputArray	src,
						OutputArray	dst,
						double		thresh,
						double		maxval,
						int			type)

将其中的第5个参数type指定为THRESH_OTSU就是Otsu算法。
这个函数也可以用来通过将该参数指定为THRESH_BINARY来使用固定阈值的方法。
以下是Otsu算法的一个结果示例(上：原图，中：直方图，下：二值化后的结果）：

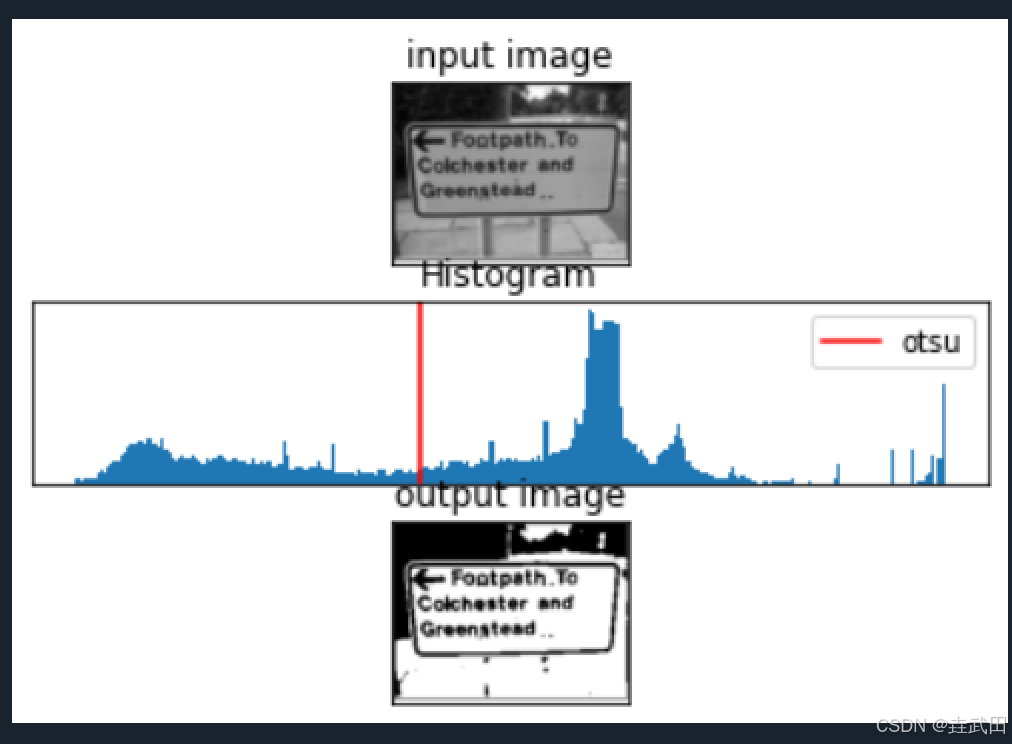
直方图中的红色竖线为Otsu算法找出的最佳阈值。