文章目录
- 引言
- 正文
- 一面
- 说一下堆排序
- 二面
- 有了解过游戏后端应该是干什么的吗?
- 博客是从什么时候开始写的?
- 平常在哪里做题?做了多少题?
- 给你二维矩阵,零代表可以走,一代表不可以走,从起点到终点,计算一下最短路径。
- 你说用到了动态规划,这个题可以使用动态规划吗?
- 如果你非要说能够使用动态规划,状态转移方程怎么写?
- 这个题目可以使用广度优先搜索吗?
- 广度时间复杂度是多少?
- BFS求路径怎么做到?
- DFS怎么保存路径?
- 时间复杂度太高了怎么办?
- 先讲一个背包问题,无限个不同面值的硬币,问你能不能凑出来一个特定的面额!
- redis你怎么学的?redis的持久化有哪些?
- redis持久化怎么修改配置?
- 在项目中是怎么实现分布式锁的?
- 补充
- 迷宫问题
- 深度优先搜索怎么做?如何保存路径!
- 广度优先搜索实现?计算最短路径并保存具体的路径!
- DP类型的迷宫问题实现
- 背包问题的推导和优化
- redis持久化具体怎么配置
- RDB持久化配置
- AOF快照配置
- StringBuilder、StringBuffer和String
- 总结
引言
- 莫名其妙过了一面,而且一面并没有问什么东西。
正文
一面
说一下堆排序
二面
有了解过游戏后端应该是干什么的吗?
- 没有细致了解过,简单说了一下自己玩过的游戏。
博客是从什么时候开始写的?
- 退伍之后开始写的,写了差不多五六年!写的最多的还是数据结构(真不该这样说,下面就开始问我算法了,给我整的有点懵逼)
平常在哪里做题?做了多少题?
- leetcode做了200道题,acwing做了三百多题,然后说了DP的相关内容,树形DP、区间DP、状态转换机 等(下面就开始问这个了,尴尬!)
给你二维矩阵,零代表可以走,一代表不可以走,从起点到终点,计算一下最短路径。
- 迷宫问题常见方式是二维DP和回溯来实现(这里两种方法实现差异弄错了,能不能用DP只能说先定方向。)
你说用到了动态规划,这个题可以使用动态规划吗?
- (完全说错了,这里上下左右说明子状态还没有推导出来,所以不能用动态规划,我全程在胡扯!!)
- 迷宫问题,固定方向可以使用动态规划,这里没有规定方向,不能使用动态规划。
- 尴尬,这里沉默了大概五分钟,肯定会挂的,我还在这里强!无语!我又跟他争辩了十分钟!无语!
如果你非要说能够使用动态规划,状态转移方程怎么写?
- 一下子顿悟了,不能使用动态规划!他说了方程才明白!
这个题目可以使用广度优先搜索吗?
- 可以使用光度优先搜索,大概说了一下过程,但是广度优先搜索的怎么获取最短路径说的不够详细,然后怎么计算最短路径哪里没说好!
- 又沉默了五分钟!完全没必要,肯定能够做的!
- 这里又提到了使用交换队列,来计算路径,然后通过父节点的索引,来计算路径!
广度时间复杂度是多少?
- 还是平方
BFS求路径怎么做到?
- 有沉默!这个不应该沉默!
- 然后扯到了之前参加的华为软件精英挑战赛,扯了一通,我忘记怎么计算最短路径了,怎么求出来的!过的有点久!尴尬!
DFS怎么保存路径?
时间复杂度太高了怎么办?
- 加上一些A星启发式算法!
先讲一个背包问题,无限个不同面值的硬币,问你能不能凑出来一个特定的面额!
- 写了一下DP的状态转换方程,但是这里直接写了公式优化的模式,而且他问的是能不能,不是最少的硬笔数,能不能应该还是使用或|,这里还是得好好过一下!
redis你怎么学的?redis的持久化有哪些?
- 看黑马程序员学的,三周学完了
- 这个八股说的很详细,这里就不写了!
redis持久化怎么修改配置?
在项目中是怎么实现分布式锁的?
- 怎么用redis的,直接调用jedis相关指令,使用现成的东西,并没有深究,
补充
迷宫问题
深度优先搜索怎么做?如何保存路径!
- DFS我还是会写的,这里是使用递归实现的,然后保存路径也是单独通过一个变量实现的。
import java.util.*;
public class Main {
private static final int[][] DIRECTIONS = {{0, 1}, {1, 0}}; // 右和下两个方向
private static int minSum = Integer.MAX_VALUE; // 用于存储最小路径和
private static String minPath = ""; // 用于存储最小路径
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int count = in.nextInt();
while (count > 0) {
count--;
int x = in.nextInt();
int y = in.nextInt();
int[][] grid = new int[x][y];
for (int i = 0; i < x; i++) {
for (int j = 0; j < y; j++) {
grid[i][j] = in.nextInt();
}
}
// 开始DFS搜索
dfs(grid, 0, 0, 0, new StringBuilder());
// 输出最小路径和及其路径
System.out.println("Minimum Path Sum: " + minSum);
System.out.println("Path: " + minPath);
}
in.close();
}
private static void dfs(int[][] grid, int i, int j, int currentSum, StringBuilder path) {
int x = grid.length;
int y = grid[0].length;
// 更新当前路径和路径字符串
currentSum += grid[i][j];
path.append("(").append(i).append(",").append(j).append(") ");
// 如果到达右下角终点
if (i == x - 1 && j == y - 1) {
if (currentSum < minSum) {
minSum = currentSum;
minPath = path.toString();
}
} else {
// 向下或向右继续探索
for (int[] dir : DIRECTIONS) {
int ni = i + dir[0];
int nj = j + dir[1];
if (ni >= 0 && ni < x && nj >= 0 && nj < y) {
dfs(grid, ni, nj, currentSum, path);
}
}
}
// 回溯: 移除路径中当前节点
path.setLength(path.length() - 6); // 撤销最后一个坐标 "(i,j) "
}
}
总结
-
DFS最好还是使用递归实现,然后记得恢复现场
- 时间复杂度
- 这个丢人丢大了,每次都是选择两个方向,然后每次操作都应该是2的 m + n次方,是一个指数级的操作,我还说是平方级,真的丢人。
- 空间复杂度
- m + n因为每一个节点都需要由递归调用栈
- 时间复杂度
-
path.setLength(path.length() - 6); // 撤销最后一个坐标 "(i,j) “
-
setLength截取StringBuffer的特定长度
广度优先搜索实现?计算最短路径并保存具体的路径!
import java.util.Scanner;
import java.util.*;
public class Main{
private static final int[][] DIRECTIONS = {{0,1},{1,0}};
public static void main(String args[]){
Scanner in = new Scanner(System.in);
int count = in.nextInt();
while(count > 0){
count --;
int x = in.nextInt();
int y = in.nextInt();
int[][] grid = new int[x + 1][y +1];
for(int i = 0;i < x;i ++){
for(int j = 0;j < y;j ++){
grid[i][j] = in.nextInt();
}
}
// 使用dp进行遍历
// 队列中的每一个元素是一个数组{i,j,currentSum,pathIndex}
Queue<int[]> q = new LinkedList<>();
// dp和path用于保存最小路径
int[][] dp = new int[x][y];
String[][] paths = new String[x][y];
// 初始化dp和paths
for (int i = 0;i < x;i ++)
Arrays.fill(dp[i], Integer.MAX_VALUE);
dp[0][0] = grid[0][0];
paths[0][0] = "(0,0)";
// 队列加入初始元素
q.add(new int[]{0,0,grid[0][0]});
while (!q.isEmpty()){
int[] cur = q.poll();
int i = cur[0],j = cur[1],curSum = cur[2];
// 遍历所有方向
for(int[] dir : DIRECTIONS){
int ni =i + dir[0];
int nj =j + dir[1];
// 计算目标点的距离
if(ni >= 0 && ni < x && nj >= 0 && nj < y){
int newSum = curSum + grid[ni][nj];
// 如果新的路径和更小,则更新
if (newSum < dp[ni][nj]){
dp[ni][nj] = newSum;
paths[ni][nj] = paths[i][j] + String.format("(%d,%d)",ni,nj);
q.add(new int[]{ni,nj,newSum});
}
}
}
}
// 输出dp数组
for (int i = 0;i < x;i ++){
for (int j = 0;j < y;j ++){
System.out.print(dp[i][j] + " ");
}
System.out.println();
}
// 输出最小路径
System.out.println("Minimum Path sum " + dp[x - 1][y - 1]);
System.out.println("Path " + paths[x - 1][y - 1]);
}
in.close();
}
}
总结
- 单纯DP,队列中的一个元素,是每一个点的坐标
- 保存最短路径长度,需要创建一个路径长度矩阵,和原来的矩阵同样大小,然后逐个进行比较
- 保存具体路径,需要维系一个具体路径矩阵,然后输出最后的坐标。
- 上述三个步骤是递增的,如果要获取具体最短路径,就是需要创建一个具体的长度距离矩阵,然后进行计算比较。通过这个坐标点比较确定最短路径的。
- 时间复杂度是n的平方
DP类型的迷宫问题实现
- 最基本的摘花生,具体题目如下,这个就是经典的可以使用DP解决的迷宫问题,因为限定了方向,所以可以使用DP解决,因为子状态是固定的

这里就有两种代码,一种是没有扩充边界的初始值情况,一种是有边界初始值的情况,具体如下
import java.util.Scanner;
import java.util.*;
public class Main{
public static void main(String args[]){
Scanner in = new Scanner(System.in);
int count = in.nextInt();
while(count > 0){
count --;
int x = in.nextInt();
int y = in.nextInt();
int[][] grid = new int[x + 1][y +1];
for(int i = 0;i < x;i ++){
for(int j = 0;j < y;j ++){
grid[i][j] = in.nextInt();
}
}
// 使用dp进行遍历
int[][] dp = new int[x + 1][y + 1];
dp[0][0] = grid[0][0];
for(int i = 0;i < x;i ++){
for(int j = 0;j < y;j ++){
if(i > 0) dp[i][j] = Math.max(dp[i - 1][j] ,dp[i][j])+ grid[i][j];
if(j > 0) dp[i][j] = Math.max(dp[i][j] ,dp[i][j - 1]+ grid[i][j]);
//
}
}
for(int i = 0;i < x;i ++){
for(int j = 0;j < y;j ++){
System.out.print(dp[i][j] + " ");
}
System.out.println();
}
System.out.println(dp[x - 1][y - 1]);
}
}
}
注意,这里一定要初始化x = 0和y=0,也就是初始值的情况。否则会出现异常,因为没有计算到最初值的情况
import java.util.Scanner;
import java.util.*;
public class Main{
public static void main(String args[]){
Scanner in = new Scanner(System.in);
int count = in.nextInt();
while(count > 0){
count --;
int x = in.nextInt();
int y = in.nextInt();
int[][] grid = new int[x + 1][y +1];
for(int i = 1;i <= x;i ++){
for(int j = 1;j <= y;j ++){
grid[i][j] = in.nextInt();
}
}
// 使用dp进行遍历
int[][] dp = new int[x + 1][y + 1];
for(int i = 1;i <= x;i ++){
for(int j = 1;j <= y;j ++){
dp[i][j] = Math.max(dp[i - 1][j] ,dp[i][j - 1])+ grid[i][j];
}
}
System.out.println(dp[x ][y ]);
}
}
}
使用这种方式效果会更好,因为在地图矩阵周围又扩了一圈,不用担心会越界!
import java.util.Scanner;
import java.util.*;
public class Main{
public static void main(String args[]){
Scanner in = new Scanner(System.in);
int count = in.nextInt();
while(count > 0){
count --;
int x = in.nextInt();
int y = in.nextInt();
int[][] grid = new int[x + 1][y +1];
for(int i = 0;i < x;i ++){
for(int j = 0;j < y;j ++){
grid[i][j] = in.nextInt();
}
}
// 使用dp进行遍历
int[][] dp = new int[x + 1][y + 1];
int[][] path = new int[x + 1][y + 1];
dp[0][0] = grid[0][0];
path[0][0] = -1; // path仅仅是用来保存方向的
// 当y等于零,初始化第零列
for(int i = 1;i < x;i ++) {
dp[i][0] = dp[i - 1][0] + grid[i - 1][0];
path[i][0] = 0;// 从上面来
}
// 当x等于零,没有办法减一
for(int j = 1;j < y;j ++){
dp[0][j] = dp[0][j - 1] + grid[0][j];
path[0][j] = 1; // 从左边来
}
for(int i = 1;i < x;i ++){
for(int j = 1;j < y;j ++){
if(dp[i - 1][j] > dp[i][j - 1]){
dp[i][j] = dp[i - 1][j] + grid[i][j];
path[i][j] = 0;
}else{
dp[i][j] = dp[i - 1][j - 1] + grid[i][j];
path[i][j] = 1;
}
}
}
// 回溯遍历最终的终点
System.out.println("Path:");
int i = x- 1,j = y - 1;
StringBuilder pathStr = new StringBuilder();
while (path[i][j ] != -1){
if(path[i][j] == 1){
// 来自于上面的格子
pathStr.insert(0,"right ");
j --;
}else{
pathStr.insert(0,"down ");
i --;
}
}
pathStr.insert(0,"(0,0)");
System.out.println(pathStr.toString());
}
}
}
分析
- 这里是创建了一个path,用来记录每一次做出决策的具体内容,而不是对应的点,因为这里每一个状态都是由子状态决定的,并并不是记录点就行了,或者说孤立的一个点!最后在从终点,逆序推导出最终的目标点的路径!

背包问题的推导和优化
- 这里放一道题,是一个典型的完全背包问题,以往做的链接,关于朴素做法我是知道的, 但是关于推导公式当时就没有写出来
- 买书——第一次做
- 买书——第二次做
- 买书——第三次做
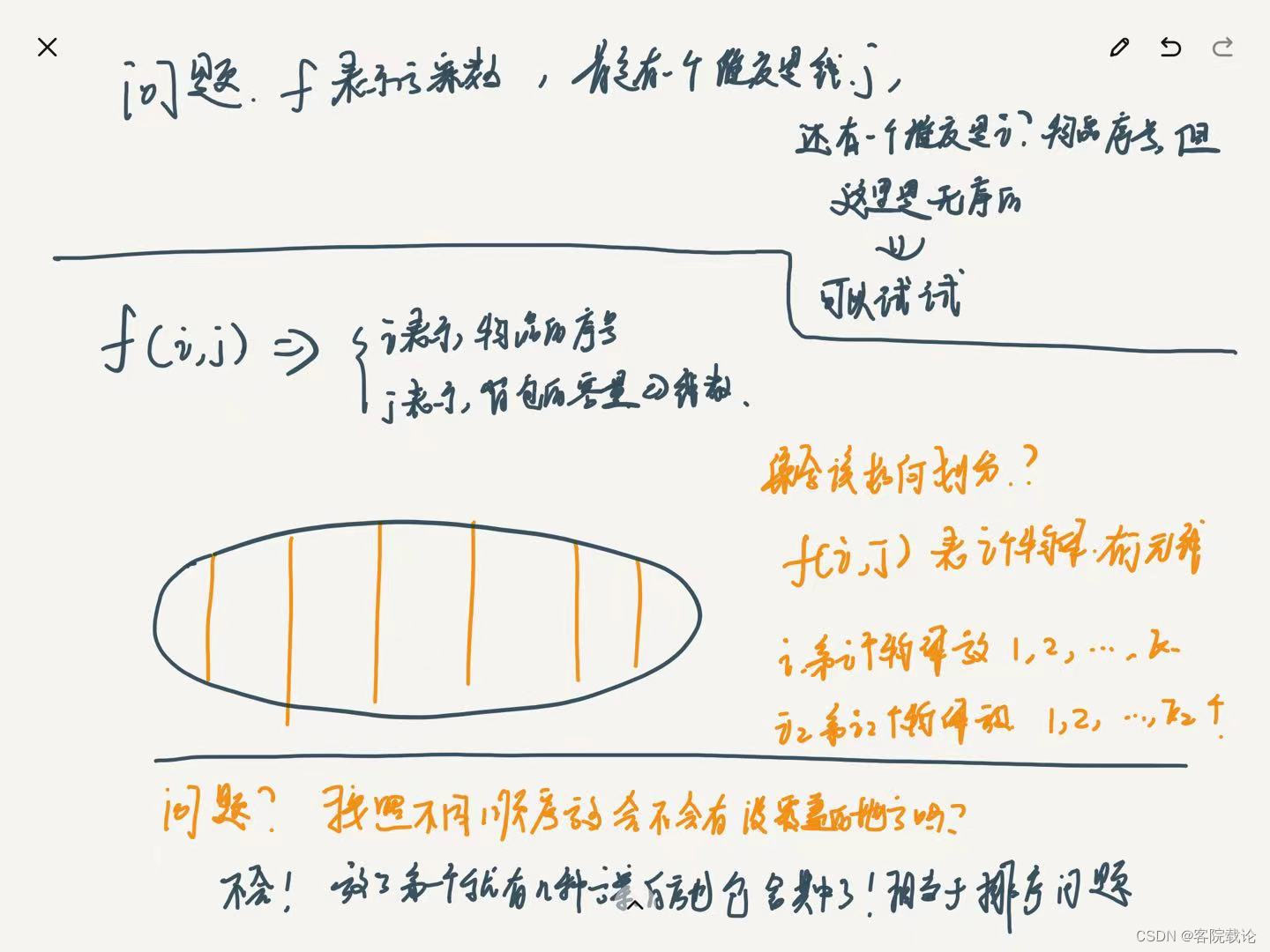
- 这里使用集合的角度进行思考,n个物体和s个背包容量,从一个角度出发,物体的角度出发,就是按照物体的次序,对结果进行划分,每一个物体又可以放零个或者n个,这里就需要处理一下

根据这个公式可以知道,在逐次遍历的过程中,可以使用公式进行优化,具体实现如下
方案一:未经过优化,原始数组
import java.util.Scanner;
import java.util.*;
class Main{
public static void main(String args[]){
Scanner in = new Scanner(System.in);
int m = in.nextInt();
int booksNum = 4;
int[] books = {0,10,20,50,100};
// 创建二维DP数组
int[][] dp = new int[5][m + 1];
dp[0][0] = 1;
for(int i = 1;i <= booksNum;i ++){
for(int j = 0;j <= m; j ++){
for(int count = 0;count * books[i] <= j;count ++){
dp[i][j] = dp[i][j] + dp[i - 1][j - count * books[i]];
}
}
}
System.out.println(dp[4][m]);
}
}
上述版本就是完全没有使用任何优化,因为每一次递归的时候,都可能摆放n个物体,然后逐个进行递增,单纯按照集合推导的角度进行出发的!
方案二:经过优化,但是没有使用滚动数组优化
- 根据之前推导的公式,可以使用f[i][j - vi]进行优化
import java.util.Scanner;
import java.util.*;
class Main{
public static void main(String args[]){
Scanner in = new Scanner(System.in);
int m = in.nextInt();
int booksNum = 4;
int[] books = {0,10,20,50,100};
// 创建二维DP数组
int[][] dp = new int[5][m + 1];
dp[0][0] = 1;
for(int i = 1;i <= booksNum;i ++){
for(int j = 0;j <= m; j ++){
if(j - books[i] < 0)
dp[i][j] = dp[i - 1][j];
else
dp[i][j] = dp[i - 1][j] + dp[i][j - books[i]];
// for(int count = 0;count * books[i] <= j;count ++){
// dp[i][j] = dp[i][j] + dp[i - 1][j - count * books[i]];
// }
}
}
System.out.println(dp[4][m]);
}
}

不能直接写成如下形式,因为当前行的状态,是需要借鉴当前行容量以前的状态,如果不更新就是零了

方案三:最终的优化版本
import java.util.Scanner;
import java.util.*;
class Main{
public static void main(String args[]){
Scanner in = new Scanner(System.in);
int m = in.nextInt();
int booksNum = 4;
int[] books = {0,10,20,50,100};
// 创建二维DP数组
int[] dp = new int[m + 1];
dp[0] = 1;
for(int i = 1;i <= booksNum;i ++){
for(int j = books[i];j <= m; j ++){
dp[j] = dp[j] + dp[j - books[i]];
}
}
System.out.println(dp[m]);
}
}
滚动数组优化,上述代码使用了滚动数组优化,因为每一次都使用同一行,而且更新仅仅会调用之前的列,具体如下图!

redis持久化具体怎么配置
RDB持久化配置
-
编辑redis.conf进行配置
- save 900(时间范围) 1(数据发生修改的频次阈值)
-
配置保存路径并指定rdb存储路径
- 配置写入RDB持久化失败之后,阻止redis再进行写入操作
dir /path/to/dump-directory/
dbfilename dump.rdb
stop-writes-on-bgsave-error yes
AOF快照配置
- 在redis.conf文件中配置,打开AOF快照
appendonly yes - 配置AOF文件名
appendfilename "appendonly.aof"
- 设置写入频率
# always: 每次有写操作时都同步(最安全,但性能最低)
# everysec: 每秒同步一次(推荐,性能和数据安全的平衡)
# no: 由操作系统决定何时同步(性能最好,但可能会丢数据)
appendfsync everysec
- 设置重写AOF文件条件
auto-aof-rewrite-percentage 100
auto-aof-rewrite-min-size 64mb
上述左右操作都需要重启redis进行配置
StringBuilder、StringBuffer和String
-
String
- 不可变形,每次对其进行拼接或者修改,都是创建一个新的String对象
- 频繁创建和修改消耗性能的。
- 线程安全的
-
StringBuiler
- 可变的,可以在原有对象上修改,不会生成新的对象
- 内部使用一个可扩展的字符数组来存储字符串内容,拼接是在末尾追加字符,效率更高
- 线程不安全的,适合单线程的操作
-
StringBufer
- 可变的,内部使用可扩展的字符数组,拼接和删除都是修改对应的字符串
- 线程安全的,内部每一个方法都是使用Synchronized修饰的!
总结
-
兄弟,千万不要说的太满了,这个友塔游戏纯纯翻车,什么都不会,被人家看穿了,我是做过,但是脑子记性不好,忘得差不多了!
-
人家还是很想要你的,一直在给你机会,但是你说的确实不是很好,甚至说有点糟糕,无论是是吹了很多次的算法,还是八股的相关设置问题的。
- 你说你的算法能力很强,但是我问了好几个,你还是不会!
- 你说你做过项目,问了你一些基本的设置,你也说不知道!
-
最后还在狡辩,说我没说错,是你说错了,真的印象差极了,真的没有必要这样的!还是不行,为人处事还是说话能力都不行!
8/12
- 读了一些书,心境发生了变化,觉得这些都不算什么,尽力就行,成功或者失败都是一种体验,活着就是人生最大意义!